智力型数学潜优生的个案研究

胡倩洁

【摘要】本文以潜优生为研究对象，采用个案研究的方法，选择典型案例分析初中数学潜优生的成因及转化策略。

【关键词】智力型潜优生 个案研究 成因 转化策略

初中数学

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2019）07A-0010-02

在实际的学习过程中，尤其是进入初中阶段以来，学生在学习成绩、学习兴趣、学习方法等方面开始出现较大的差异，慢慢形成了“尖子生”“中层生”“潜力生”三种不同类型的学生。在大多的教学过程中，教师存在“抓两头带中间”的弊端，即教师花大部分的精力在培养尖子生、转化潜力生、带动中层生三大方面，而往往忽略了处在“尖子生”和“中层生”之间的临界生，也就是本文将要研究的“潜优生”。

潜优生是最容易被忽略，却值得被重视的一部分群体。他们接近于“尖子生”，但与“尖子生”又有差距，他们有潜力、有可塑性，但是存在波动大不稳定、反复性强等特点。目前关于潜优生的研究主要是针对群体的研究，针对个案进行深入研究的案例较少。找到“潜优生”和“尖子生”在智力因素方面的差距，分析“潜优生”的成因和转化策略，能为学校和教师采取干预措施提供理论参考。本研究采用个案研究的方法，基于智力因素，选择典型案例来分析初中数学潜优生的成因及转化策略。

一、潜优生的背景

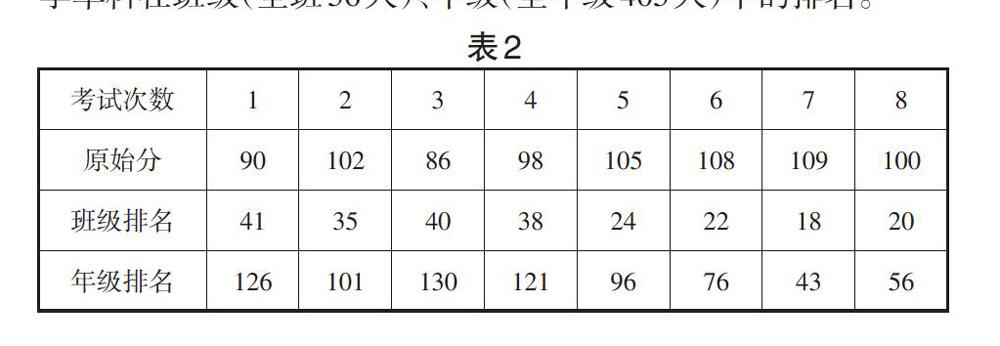
学生小罗，上课认真听课，按时完成作业，不懂的问题能及时请教老师和同学，语文、英语成绩不错，但是她却不属于优生之列，原因很简单，她的数学成绩长期在80分到90分之间，数学单科成绩常常使得她只能在年级100名左右徘徊。

二、潜优生数学学习效率不高的主要表现

（一）理解记忆成分较低。小罗认为，“数学是理科，不需要像语文、英语那样记忆”。因此，在学习基本概念、定理、法则和常用的数学思想方法时，她总是不以为然，无意学习占据了的主导地位。

（二）模仿能力较强，但变通能力不够，方法单一，缺乏灵活性。小罗能模仿教师给出的例题，完成同一类型的练习，但是例题稍有改动就措手不及，很难联想数学知识之间的联系，孤立、静止地对待数学问题，思维角度较狭窄，思维较僵化。像小罗这种类型的潜优生属于智力型数学潜优生，往往因为自己在思维力和记忆力方面存在一些障碍，影响数学成绩的进步。这类型的学生，通常能达到基本的数学要求，但是在记忆力和思维力方面，仍然有很大的进步空间。

三、潜优生数学学习障碍的成因分析

（一）智力因素的影响。从小罗平时的表现来看，她在记忆力和思维力方面是不如尖子生的，对数学概念、定理和基本思想方法缺乏基础的记忆，又不善于整理、归纳知识，还缺乏一定的思维发散、迁移能力。但是，从平时观察来看，小罗在其他智力方面的能力，如对于数学问题的阅读能力、观察能力还是相当不错的。

（二）原有的知识贮备不完善。数学知识是严谨、有逻辑序列的，数学学习的过程是循序渐进和连续的。学生在学习过程中，把前面的知识遗忘了，或者根本没学懂，就会在学习新知识的过程中、在同化新旧知识时存在困难，如果不及时弥补，就会给学习带来困难，久而久之便形成恶性循环。

（三）潜优生的认识存在问题。像小罗一样，很多学生心中容易有“数学是理科，不需要像文科那样记忆”的想法，这就是学生对数学学习的认识存在问题。正是因为学生有如此想法，学生在学习数学概念、定理和基本思想方法时，容易产生无意学习，对数学基础知识的理解、记忆、认识不到位，不深刻，导致知识掌握得不稳固，引起后续的知识储备的缺失。

（四）学习方法不当。“会学”和“学会”是两种不同的境界，尤其对于九年级的学生来说，要同时面对多个考试科目，作业量大，要“学会”多种多科知识已属不易，合理安排时间、科学用脑，让“死学”变成“活学”“会学”，才能在有限的时间内取得进步。

四、潜优生克服数学学习障碍的策略

（一）训练其复述策略。由于小罗的记忆力并不好，刚学习的知识都容易遗忘，在解题过程中会把题意部分遗忘和曲解，导致解题偏差，而这些都与未能深刻理解题意有关。在训练过程中，笔者引导小罗复述题意，让她在对题目分解、复述、再剖析的过程中，把短时记忆中的题意转入较长时间的记忆中，使其在解题过程中不会忘记题目的要求。

（二）加强其对数学概念、定理和基本思想方法的记忆。在教学的过程中，笔者会刻意关注小罗对于数学基础知识的记忆训练，检查其记忆的效果，并不定期进行特定检测。在检测的过程中，除了单一的概念背诵检测，还会有多层次的检验，设置不同难度的题目来对同一知识点进行测试，掌握其对同一知识点的理解程度。

（三）补充知识点，弥补知识储备的不足。笔者在测试中发现，小罗对代数和统计知识掌握得不错，但是对几何逻辑推理的题目，明显掌握不足，甚至有点无从下手。比如，在复习证明平行四边形的过程中，一开始，小罗混淆了能够证明平行四边形的几种基础方法，这是明显的知识储备的问题。因此，在复习的过程中，笔者先引导小罗整理现已掌握的知识点，发现她能清楚列举出证明平行四边形的五种方法（证明两组对边平行、两组对边相等、两组对角相等、两条对角线互相平分、一组对边平行且相等），但是在面对数学题目时，却不知道选用哪一种方法进行证明。因此，笔者引导她剖析题意，分析题目现有的、可直接证明的条件和缺乏的条件，根据直接条件，确定方法方向，再从间接条件中寻找可转化成直接条件的依据，找到证明的方法。

例如，已知：如圖，在四边形ABCD中，AB∥CD，对角线AC、BD相交于点O，BO=DO。求证：四边形ABCD是平行四边形。

解题步骤1：题目中有①条件AB∥CD，根据“两组对边平行”或“一组对边平行且相等”，即证明AB=CD或AD∥BC即可;②条件BO=DO，根据“两条对角线互相平分”，即证明AO=CO即可。