用问题引领初中数学复习课教学的思考
2019-10-25甘肃省天水市育生中学杜康慧
甘肃省天水市育生中学 杜康慧
一、复习课需要注重的几个要点
1.突出学生主体
数学老师在复习课堂上要创设出丰富多彩的教材知识再现形式,有的放矢地放大探究过程,赋予知识新的生命力。对于单元知识的复习要进行系统的整合,挖掘数学知识、数学方法之间的联系。这些都是在为调动学生的积极性做准备,目的是通过老师的行为带动学生参加到探究活动中去。
2.体现数学思想
数学复习课堂的教学质量与课堂体现的数学思想的高度有关。老师的复习课应该要确定一个主题,根据这个主题制定合适的教学目标,选择合适的课堂类型,将三者整合成一条教学主线。在实际教学中围绕这条主线进行教学,并且突出相关的数学思想方法,提高学生的数学素养。
3.瞄准复习要点
上好复习课的关键就是抓准复习要点,老师在教学之前要进行充分的教学准备,仔细研读文本,制定相关的教学计划。其次,在课堂上要唤起同学们的回忆,增强同学们对知识、方法的记忆程度。课堂教学之后还要加强教学研究,总结相关的教学经验,以期为下次教学提供借鉴。
二、问题在初中数学复习课上的应用
1.以问题的形式串接数学知识点
复习课堂首先复习的是数学基础知识。数学基础知识点的复习不应该是零散的,因为知识点之间存在一定的关联。而老师要做的就是找出其中的关联,并以问题的形式将其放大,吸引同学们的注意力。
例如《勾股定理》复习课的开展。勾股定理是指如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2。在实际解题过程中,还会涉及勾股定理的逆运用,即如果三角形三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,较大的边c所对应的角是直角,满足方程的三个整数叫作勾股数。为此,老师可以提出问题串帮助同学们衔接知识点,如:“勾股定理的运用对象是什么?”“这个运用对象具有哪些比较显著的性质呢?”“勾股定理的证明方式能否运用与这个对象有关的性质呢?”探究勾股定理的概念可以得出勾股定理的适用对象就是三角形,直角三角形是一种特殊的三角形。同学们回想得知,三角形具有稳定性,而且形状大小相同的图形放在一起能够完全重合,那么完全重合的两个三角形就叫作全等三角形。全等三角形对应的边,对应的角,对应边上的高、中线、角平分线,面积和周长全部都相等。证明全等三角形可以使用三个定理。其实勾股定理的证明也可以使用全等三角形的性质,以a、b为直角边,以c为斜边作两个全等的直角三角形,那么每一个三角形的面积就等于ab。把这两个三角形按照一定的方式拼接起来,可以得到一个新的三角形。从这两个三角形全等出发,探究相关的角和边的关系,可以得知这个组成的新的三角形是一个等腰直角三角形,它的面积等于c2。而这三个三角形组成的大梯形的面积是(a2+b2),然后根据面积相等就可以推出勾股定理。如此,勾股定理就和直角三角形、全等三角形联系起来了。
2.以问题为载体揭示解题方法
在复习课堂上针对有关考点进行专项复习时,老师可以设置相关的问题逐步引导学生,帮助学生由浅入深、由表及里地分析问题。进而掌握相关题型的解题方法。
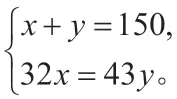
3.以问题当工具衔接实际运用
数学是一门与实际联系非常紧密的学科,新课改强调数学的教学资源应该越来越生活化,这就意味着老师要关注教学与生活的联系,将生活中的实际问题化为数学问题进行处理,缓解同学们对于数学的畏难心理。
实际生活中,最典型的问题就是彩票类的问题,这类问题与同学们的数学内容有着较为紧密的联系。其实彩票类问题在数学中就被转化为了概率类问题。例如,“某种彩票的购买以及中奖的方式是买一注彩票时任选一个6 位数,每位数字从0~9 这10 个数字中选一个,如果抽签所得到的六位数与你购买的这注彩票的六位数字相同,排列也相同,那么就中了大奖,请同学们计算这次中奖的概率是多少。”其实这考查的也是独立事件概率的计算方法。可以将其转化为“已知六位数有不同的组合方式和排列方式,求解某一特定组合和排列的六位数的概率是多少?”选定一位数字是一个独立事件,选定第一位数是中奖数的概率为,选定第二位数中奖概率也是,以此类推,选六个数中奖的概率就为。把实际问题转化为数学问题的好处在哪里呢?同学们下次在遇到实际问题时,自然而然地就会想到运用数学知识去解决问题,其实教育的初衷也就是丰富学生的知识储备,以备应对实际生活中可能出现的任何问题。因此,老师的数学复习课堂也应该出现与实际联系比较紧密的数学问题,在传授知识的同时,向学生传授一些学习经验和学习方法。
总之,很多学生在复习的时候找不到方向,难以制定相关的复习策略,导致复习效率低下。这时老师的复习课就要充分发挥引导作用,引导学生进行复习,使同学们收获到良好的复习效果,以便于更好地应对考试。
