基于VHDL的自适应滤波器的设计与实现

吕 虹，蒋婷婷，肖 曼

(安徽建筑大学 电信学院，安徽 合肥 230601)

自适应滤波器在现代数字信号处理中应用极为广泛[1]。滤波器是人们进行设计系统的一种术语，是为了能够从已经失真的信息中过滤出实施者所需要的接近原本的有用内容。由于这个措施在很多方面都会被需要，所以在众多领域都有关于这个系统的研究。

本文通过Matlab程序仿真，来探索LMS算法与FIR的联系，并通过更改步长与滤波器阶数来观察自适应滤波器收敛性能的变化。并利用了Quartus II自下向上的设计方法，选择合适的IP核，完成各项模块的设置后，通过顶层原理图将各模块连接从而实现滤波器的设计。通过Matlab的设计提供加噪声的输入数据以及原始的期望信号，最终在Quartus II上运用波形仿真文件实现滤波器的设计。

1 自适应滤波器的原理

自适应滤波器是数字滤波器的一种[2]。本文研究的是线性滤波器。对于线性自适应滤波器，一般通过输入信号(已经是目标信号加噪声之后)的自相关矩阵、误差函数等的统计特性以某一种准则为标准，使其尽可能靠向目标值的过程。图1为自适应滤波器的结构图，图中x(n)、y(n)和d(n)分别表示n时刻的输入信号、输出信号和期望信号。其中e(n)是期望信号与输出信号的误差，它能够自动地调节自适应滤波器的各项参数[3]，使下一时刻的输出y(n+1)更接近期望信号。

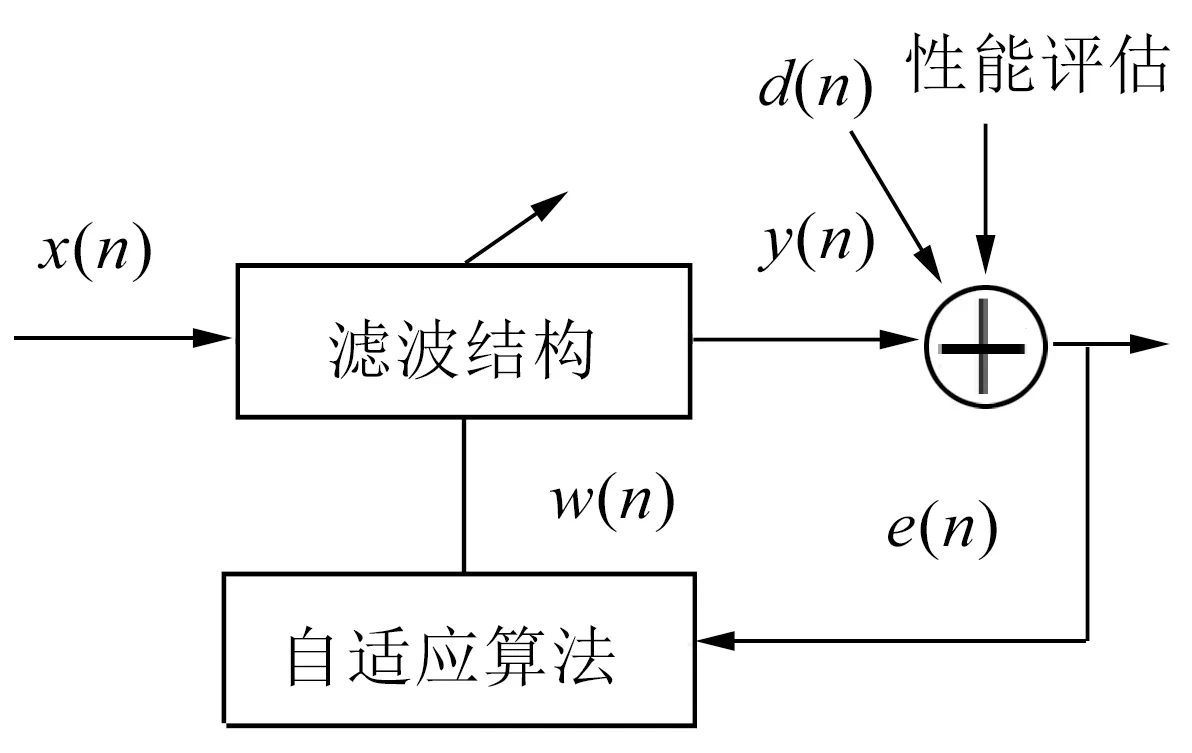
图1 自适应滤波器的结构Fig.1 Structure of adaptive filter

由图1可知自适应滤波器总共由三个部分组成，每个部分具体含义如下：

(1)滤波结构：输入信号经过滤波结构形成滤波输出。IIR滤波器具有不稳定的特点，因此本文采用了FIR滤波器进行滤波结构的设计[4]。

(2)自适应算法：通过规定的规则或函数来更改滤波器的参数，从而可以达到对应的滤波功能。

(3)性能评估：是指期望信号和输出信号的差来定义输出是否满足需求。

针对线性自适应滤波器分为两部分，一部分是滤波，另一部分是自适应[5]。自适应主要体现在：如果信号环境不发生改变时，自适应滤波器能够以逐步迭代的方式来调整滤波器系数直达到最优滤波才会停止迭代[6]。当外部信号环境发生变化时，自适应滤波器会调整滤波系数以跟踪变化。与维纳滤波器相比，自适应滤波器无需事先知道输入信号即可实现最优滤波[7]。

2 LMS算法

LMS算法作为线性自适应滤波中的梯度算法，结合最速下降算法，用瞬时平方误差代替均方误差[8]。

2.1 维纳滤波器

本文以FIR滤波器结构(也称横向结构)来介绍维纳滤波器。

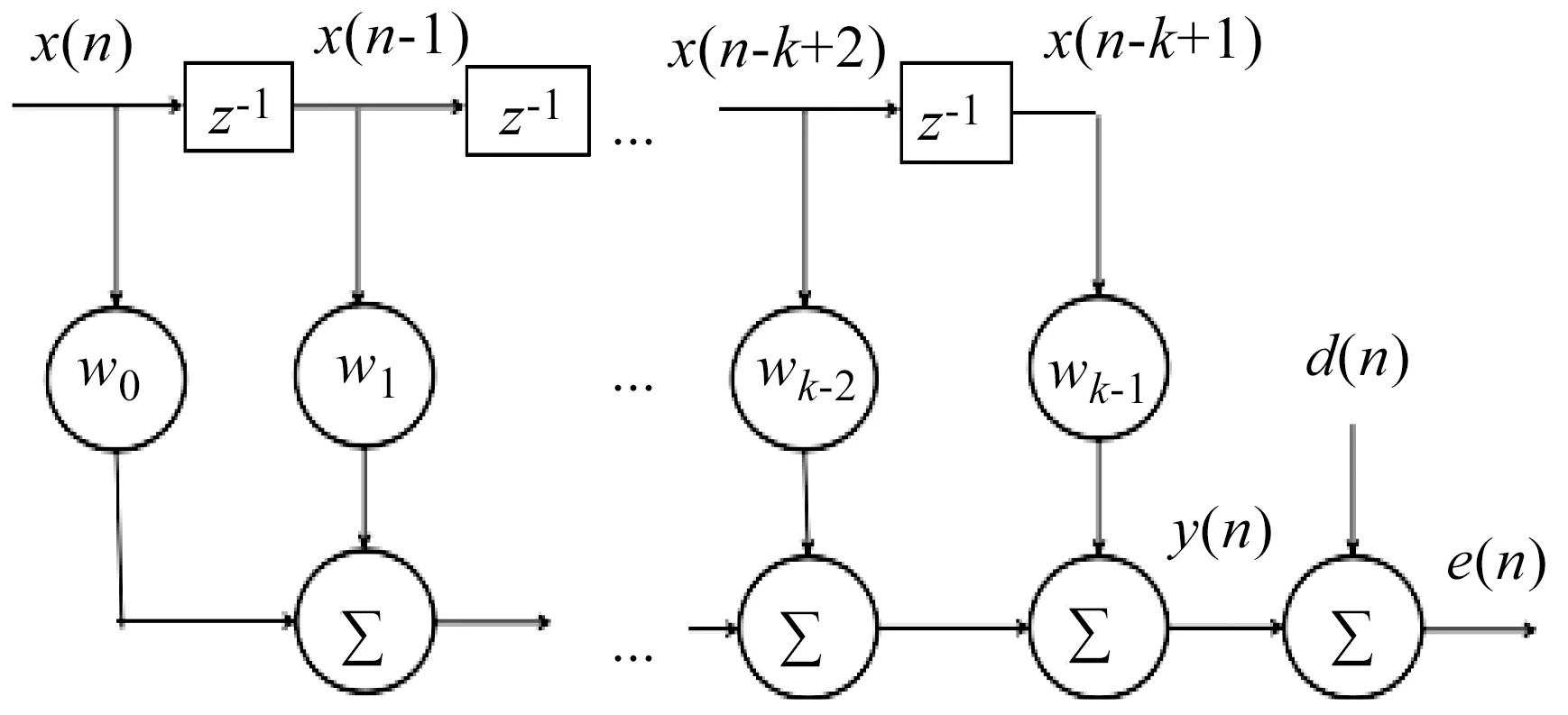
图2 FIR滤波器结构Fig.2 FIR filter structure

图2展示了k阶滤波器的横向结构图，定义如下：

(1)滤波器的输入为x(n),定义向量x(n)=[x(n),x(n-1),x(n-2),…,x(n-k+1)]T；

(2)滤波器权系数为w(n),定义向量w(n)=[w0(n),w1(n),…,wk-1(n)]T；

(3)期望信号为d(n)；

(4)滤波器的输出信号为y(n)；

(5)单位延迟单元为z-1。

x(n)通过单位延迟单元的结果是x(n-1)。当x(n)进入到滤波器之后，滤波器的输出信号y(n)为抽头输入和抽头系数的内积之和。

(1)

(1)式n为时刻，k为滤波器的阶数，wi表示第i个抽头线上的权值，x(n-i)表示n时刻横向滤波器第i个抽头线上的输入数据。系统的误差表示如下：

e(n)=d(n)-y(n)=d(n)-wT(n)X(n)。

(2)

以最小均方差为准使系统输出的均方函数J(n)达到最小，然后计算可使J(n)最小化的滤波器的权向量的值。其中，均方误差J(n)定义如下：

J(n)=E{[d(n)-wT(n)X(n)]2}。

(3)

定义输入信号的自相关矩阵为R,定义输入信号与期望信号的互相关矩阵为R,以便表示均方差函数：

R=E[X(n)XT(n)]，

(4)

R=E[d(n)X(n)]。

(5)

则式(3)式可以表示为：

J(n)=E[d2(n)]+wT(n)Rw(n)-2RTw(n)。

(6)

由(6)式可知，当输入信号与期望信号稳定时，均方误差J(n)和权向量w(n)构成了典型的二次函数。可以知道该函数的极小值是滤波器权向量的最小解，(6)对w(n)求导可得：

(7)

令(7)式为0，R为非奇异矩阵，得到如下解:

w*=R-1R。

(8)

则称w*为滤波器的维纳解。将w*代入(6)式可得均方误差函数J(n)的最小值：

Jmin(n)=E[d2(n)]-RTw*。

(9)

由上可知维纳滤波虽然可以准确地使均方误差降到最低得到最优滤波，但在求解的过程中要知道输入信号和期望信号的特性，涉及到R的求逆运算。维纳滤波缺少一个智能的、自动优化的准则可循，使其在高阶滤波中难以实现[9]，因此在此基础上进行改进。

2.2 LMS算法基本思想

根据最速下降法，沿性能表面最速下降方向(负梯度方向)调整滤波器的权值向量，以求得性能表面的最小点，这个寻找过程是一个迭代的过程[10]。设第n次迭代得到的滤波器抽头权值向量为w(n),并设该次迭代得到的均方误差是ε(n),那么第n+1次迭代得到的权向量的迭代公式为：

w(n+1)=w(n)-nu(n)。

(10)

(11)

上述选择误差性能曲面上负的梯度向量作为搜索时的方向向量的方法称为“最速下降法”。

在最速下降算法中，为了获得系统的最佳维纳解，要事先知道输入信号和期望信号的特性[11]，当期望信号未知，不能确定它们的相关特性，因此必须对梯度向量n进行估计，得到n的估计值

(12)

进一步令u(n)为常数u,则可得到新的迭代公式：

w(n+1)=w(n)+2ue(n)x(n)。

(13)

式(13)称为LMS算法。其中u可以控制算法迭代的步长，而步长的大小可以决定收敛速度，一般来说，步长越大收敛速度就会越快，反之越慢。针对具体的算法来说，为了确保算法的收敛，u不能是无限大的，要选取适合的大小。LMS算法实现滤波的步骤为：

步1初始化滤波器的参数w(0)=0；

步2给出了n时刻的输入信号向量：

x(n)=[x(n),x(n-1),x(n-2),…,x(n-k+1)]T,n时刻的期望响应是记为d(n),k称为滤波器的具体阶数；

步3计算通过滤波器的输出信号y(n)=w(n)Tx(n)；

步4比较输出信号和期望响应信号的误差e(n)=d(n)-y(n)；

步5根据误差滤波器自动的调整相应的权值向量w(n+1)=w(n)+2ue(n)x(n)。

LMS算法在计算上降低了自相关条件的要求，不需要对输入信号矩阵逆变，而且所得输出结果不断接近目标值，所以是自适应算法中稳定性比较好的，同时也是比较常用的。由于它的收敛速度和步长选择有关，步长u越大收敛速度越快。但u的范围在0至1，所以相对而言LMS的收敛速度并不快。

3 软件设计与实现

3.1 Matlab设计与仿真

实验出于对波形的方便观察，在Matlab上选择了期望信号为正弦信号，可以比较直观地观察。输入信号即待测信号是均匀分布的噪声信号加入期望信号得出，将LMS算法与FIR结构结合，即每个延迟端加入一个权头值，而LMS算法就是对权头值进行更新。而滤波输出是通过权头值与输入的卷积获得。

本文采用了蒙特卡诺(Monte Carlo)仿真方法研究了自适应滤波器的性能[12]，收敛性能纵坐标为重复次数，重复仿真得到此时在该点的误差e(n)的均方值为统计量。

(1)在相同条件下，信噪比越大，滤波的效果越好，信噪比为正时，滤波效果优于信噪比为负时，并且收敛速度较快，收敛性能也比较稳定。

(2)在其他条件不变，改变步长：三者滤波器皆为64阶，u值分别为1/256(如图3)、1/1024(如图4)、1/2048(如图5)。

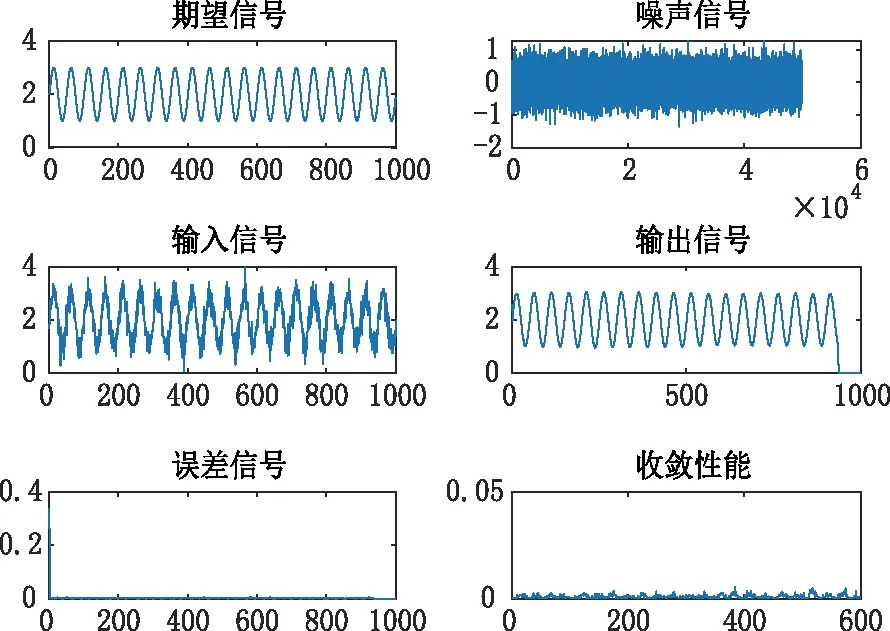
图3 k=64， u=1/256 Matlab仿真波形Fig.3 k=64， u=1/256 Matlab simulation waveform

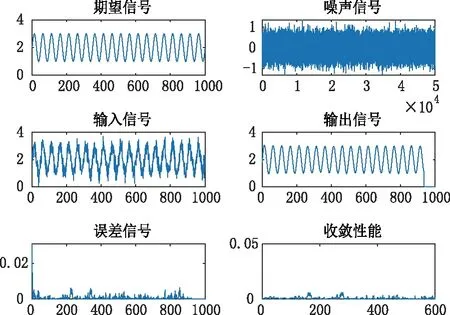
图4 k=64， u=1/1024 Matlab仿真波形Fig.4 k=64， u=1/1024 Matlab simulation waveform

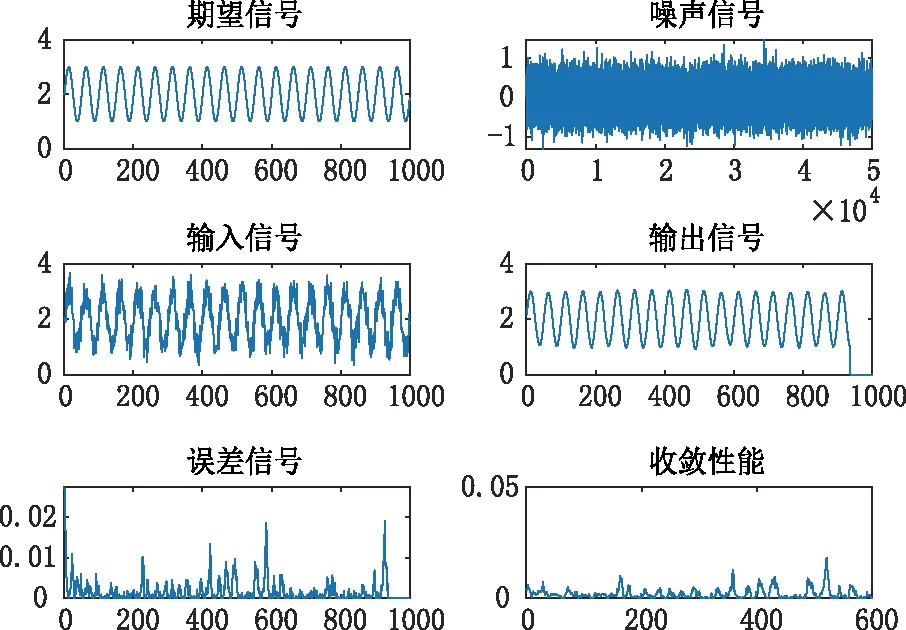
图5 k=64, u=1/2048 Matlab仿真波形Fig.5 k=64, u=1/2048 Matlab simulation waveform

可以发现当滤波器阶数不变时，步长u值越大其收敛性能越好。

(3)若u值不变时，改变滤波器阶数，u值均为1/1024，阶数分别为32(如图6)、64(如图4)、128(如图7)。

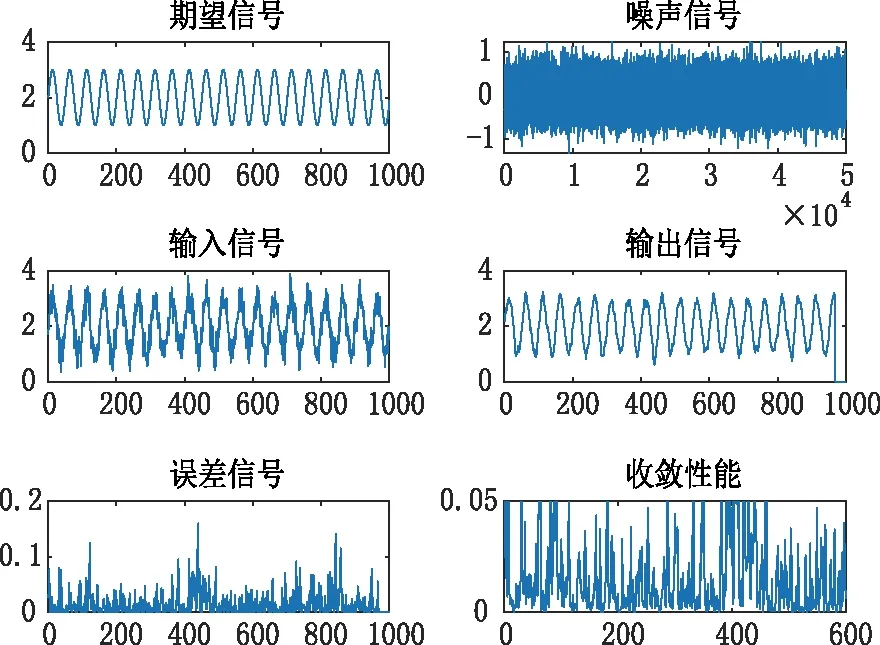
图6 u=1/1024, k=32 Matlab仿真波形Fig.6 u=1/1024, k=32 Matlab simulation waveform

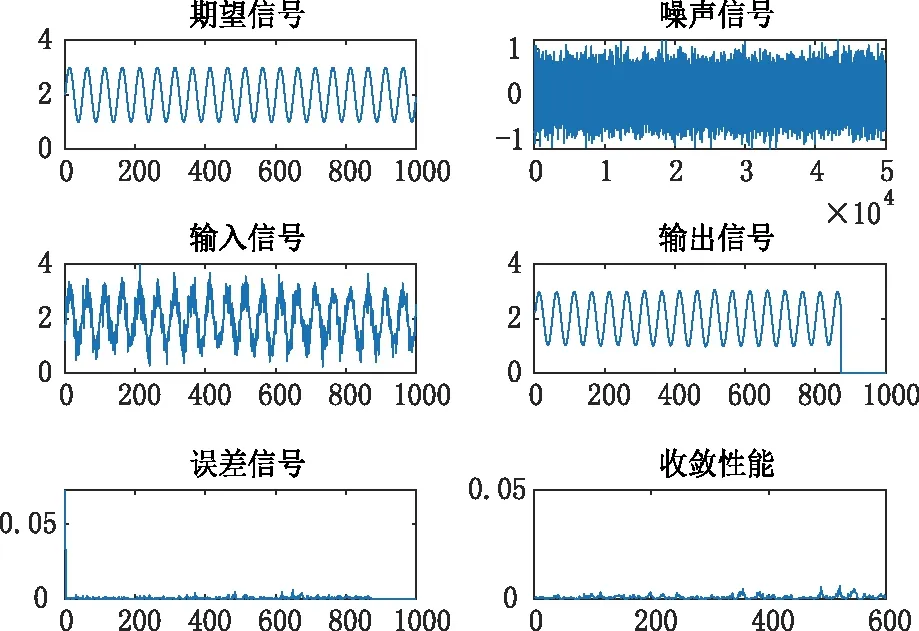
图7 u=1/1024, k=128 Matlab仿真波形Fig.7 u=1/1024, k=128 Matlab simulation waveform

可以看出，步长不变时，滤波器阶数越高其收敛性能越强。

3.2 VHDL实现主要模块设计

实验在Quartus II上通过VHDL语言编程的主模块功能主要包括了存储 、计数、乘法、卷积滤波、权值更新。由于Quartus II对数值的限制，对于Matlab上的数据选择了进行17 bit的量化。在实验过程中u值以及信噪比的选择会影响e的值可能还会导致它的高位为零，导致滤波输出为零，所以通过在Matlab中进行不断尝试，最终选择了信噪比10 db,滤波器阶数位128阶，u的值为1/1024。

对于所需要的输入，是通过Matlab获取并设置为满足Quartus II中的mif文件格式的形式，将数据转移至用记事本打开的文件的begin与end之间，后调用Quartus II的宏模块将mif文件当作其内存数据，分别生成用来存放输入信号和期望信号的存储器，生成模块如图8：

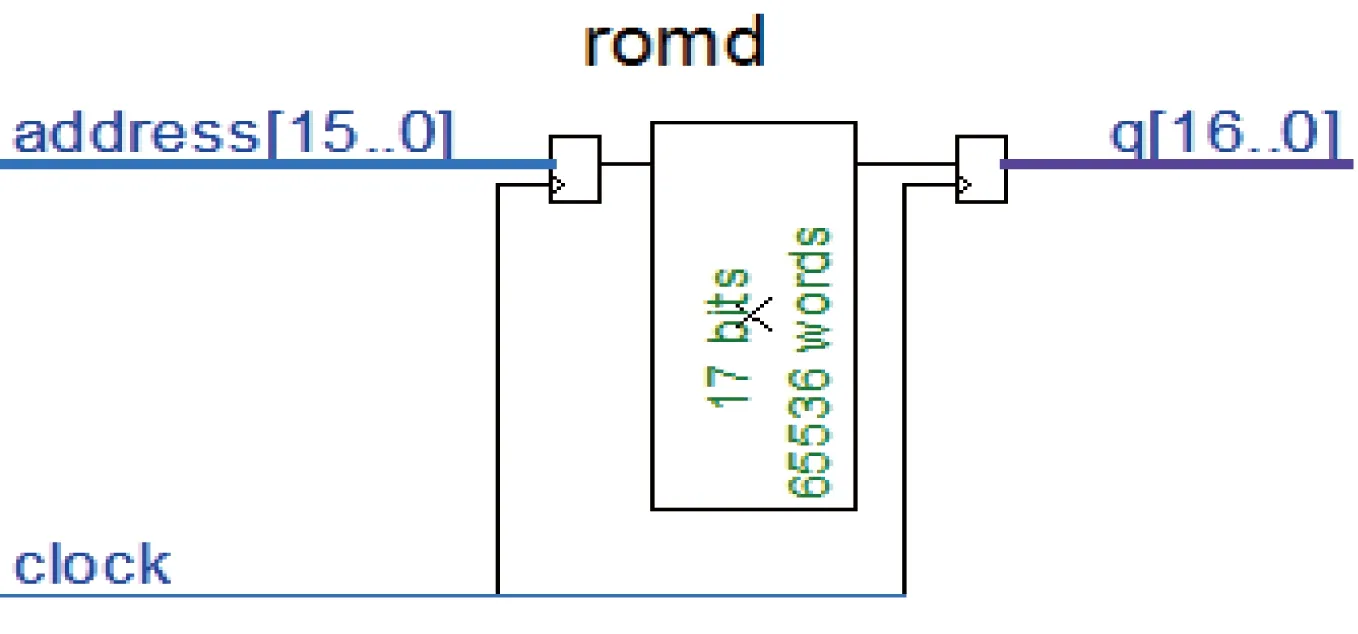
图8 期望信号模块Fig.8 Desired signal module

可以看到其输出是通过输入给地址读出信号，选择了计数器并设置updown端口，用于实现当up为1时地址不断加1，为0时地址减1的效果。如图9：

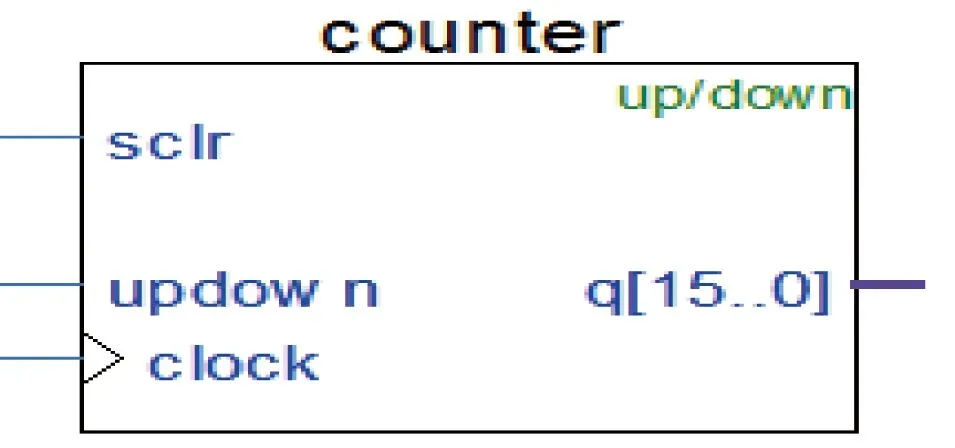
图9 输入信号模块Fig.9 Input signal module

3.3 Quartus II综合实现

Quartus II综合实现部分主要包括2个计数模块，2个rom模块和一个主模块。计数模块是用来进行计数，rom模块中romx用来存储输入信号x，romd用来存储期望信号d,主模块包括了存储 、计数、乘法、卷积滤波、权值更新。

然后建立波形文件，其中，clrd保持了20 us的“1”，后全为“0”；clrx保持了10 us的“1”,后全为“0”；为保证计数器输出一直为加1将updown一直设置为“1”。然后进行功能仿真得出波形如图10，其中x为输入信号，d为期望信号，y为滤波输出。可以看出滤波输出与期望信号相同，这与3.1节Matlab仿真结果是一致的，因此表明本文设计的滤波器功能正确，性能良好。

4 结语

本文提出的是主要基于FIR的自适应滤波器，运用了LMS算法，先在Matlab上进行操作，在达到滤波目的的同时完成对各参数的选择。在实验中，为了方便计算，步长u的值选择2的n次方的倒数，然后再改变信噪比和适合的滤波器阶数，来观察滤波效果。通过观察比较可知当信噪比为10 db,滤波器阶数为128阶，u的值为1/1024时滤波效果最好。然后在Quartus II上实现设计，对主模块数选择后，建立顶层原理图后在波形文件中观察输出，完成滤波器的设计。实验结果表明适当改变滤波器的步长和阶数可以去除噪声影响，得到最佳滤波效果。

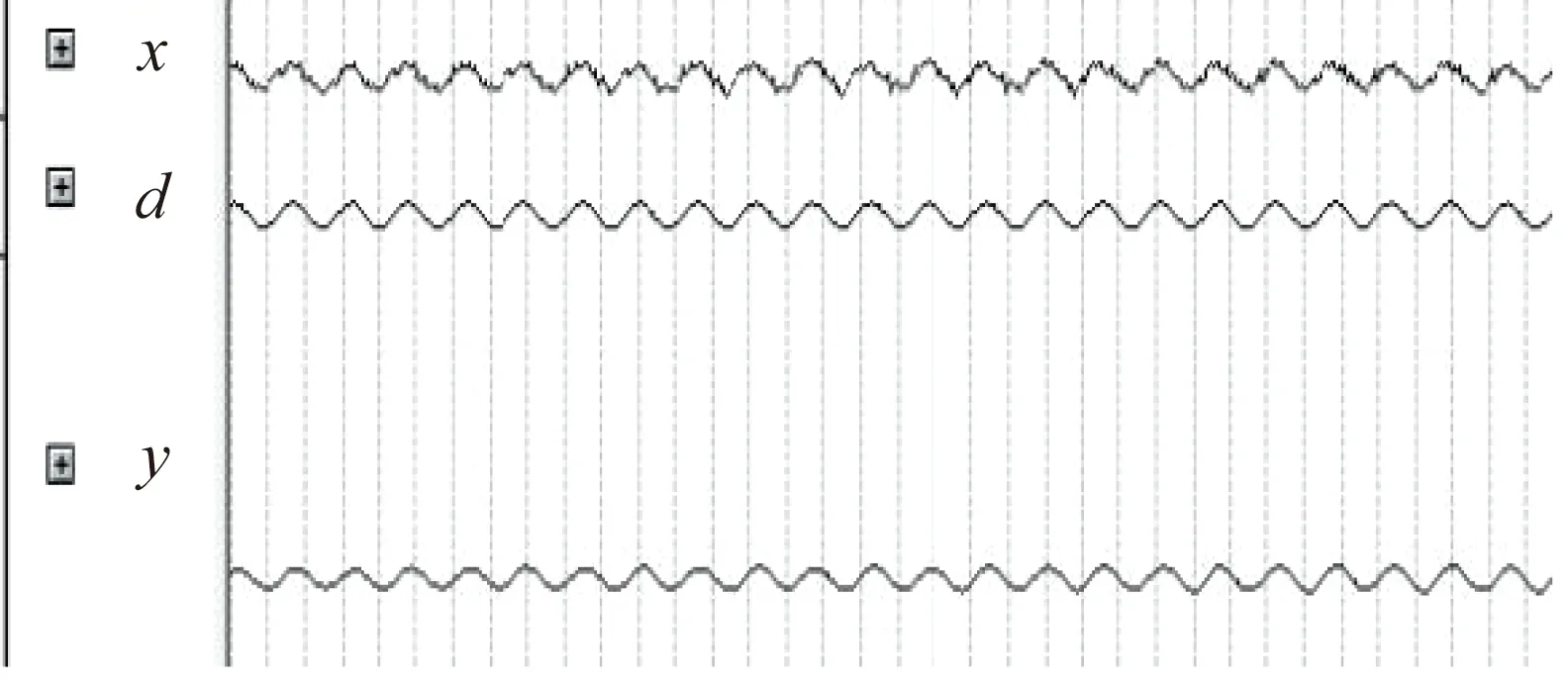
图10 Quartus II波形仿真Fig.10 Quartus II saveform simulation