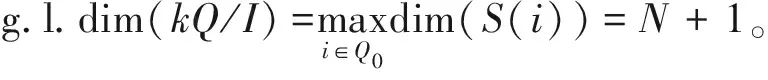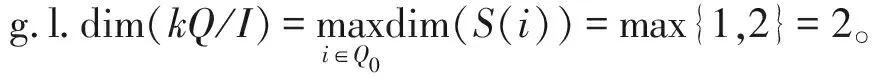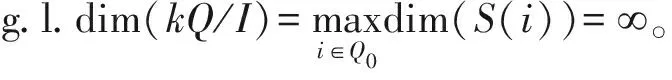两类代数的整体维数
2019-10-23杨佳佳
杨佳佳,章 超
(贵州大学 数学与统计学院,贵州 贵阳 550025)
本文中,k是代数闭域,k-代数A是有限维代数,mod-A表示代数A决定的右A-有限生成模范畴。在代数表示论中,整体维数作为重要的同调不变量之一,得到了深入研究。1987年,Schelter就利用整体维数对一些代数进行了分类,证明了整体维数为3的正则代数共分为13类[1]。1945年,Hochschild就提出Hochschild(上)同调的概念,显然,代数A的整体维数有限,则其高次Hochschild上同调是平凡的。Happle基于这一事实,考虑此结果的逆命题,即所谓的Happle问题。Happle问题对许多代数成立,如交换代数[2],单项式代数[3]。后来,韩阳研究员又提出了基于同调维数与整体维数的Han猜想[3]。由此可见,整体维数与代数的性质有密切联系。
2010年,Poettering讨论路代数kQ在不同允许理想I下的整体维数,对两类重要的代数(Poettering分别将之称为Am型代数和Xm型代数)作出讨论,证明了在特定的允许理想I下,代数kQ/I的整体维数取决于m;当Q包含定向圈时,g.l.dim(kQ/I)=[4]。后来,Happle和Zacharia针对此问题也进行了研究,进一步地定义了集合A(Q)={kQ/I| dimk(kQ/I)<且g.l.dim(kQ/I)<},并考虑sup{dimk(kQ/I)|kQ/I∈A(Q)}与sup{g.l.dim(kQ/I)|kQ/I∈A(Q)}之间的关系[5]。

1 代数整体维数
考虑文章的完整性,本节将给出代数整体维数的定义,详见参考文献[6]。
定义1.1设M是任意的右kQ/I-模,称模M的投射分解是形如这样的一条正和列P•=…→Pl→Pl-1→…→P1→P0→M→0,其中对于任意i≥0,Pi是投射模。
定义1.2对于上述定义模M的投射分解P•,若对于任意i≥l+1,Pi=0,同时对于0≤j≤l,Pj≠0,则称l是模M的投射长度,记作l(P•)=l。特别地,M的投射维数取M的所有投射分解长度的下确界infl(P•),记作p.dim(M)。此外,代数kQ/I的整体维数g.l.dim(kQ/I)=max{p.dim(M)|M是右-kQ/I模}。
下面的定理来自于文献[6]定理4.8,通过定理可以简便地计算代数kQ/I的整体维数。
定理2.1如果kQ/I是有限维k-代数,则
g.l.dim(kQ/I)=max{p.dim(S)|S是单右-kQ/I模}。
2 An型k-代数的整体维数
本节将讨论箭图为An型代数kQ/I的整体维数和理想I之间的联系。方便起见,关系p=αiαi+1…αj-1记作[i,j],其中i 定义2.1对任意关系[i,j]与[r,s],其中i 定义2.2设允许理想I=〈ps=[is,js]|s=1,…,n〉,如果允许理想I中的m个生成元ps,…,ps+m-1满足对任意正整数t∈{s,…,s+m-2},pt,pt+1相交且对任意正整数l≠t-1,t,t+1,pt,pl不相交,则称这m个关系有效相交。理想I的有效相交关系数是满足有效相交关系的最大个数,记作N。 定理 2.1设kQ/I是An型k-代数,其中允许理想I=〈ps=[is,js]|s=1,…,n〉,则代数kQ/I的整体维数为N+1,其中N是理想I的有效相交关系数。 证明:不妨假设关系pa,pa+1,…,pb的有效相交关系数为N,则存在下列不等式 ia 则对任意mod-kQ/I中单模S(ir),其中r∈N且a≤r≤b,极小投射分解形如 0→P(jb)→P(jb-1)→…→P(jr+1)→P(jr)→P(ir+1)→P(ir)→s(ir)→0, 于是p.dim(S(ir))=b-r+2≤N+1。特别地,当r=a时,等号成立。 若存在其他的有效相交关系pu,pu+1,…,pv,对于单模S(it),其中t∈N且u≤t≤v,p.dim(S(it))=v-t+2≤N+1。特别地,若关系pu,pu+1,…,pv的有效相交关系等于N,此时当t=u时,等号成立。 对于其余单模S(i),其中i∈Q0{ir|r∈N,1≤r≤n},极小投射分解形如 0→P(i+1)→P(i)→s(i)→0, 可知p.dim(S(i))=1。 综上所述, 根据定理2.1,显然有以下结论。 推论2.1设kQ/I是An型k-代数,其中I=〈ps=[is,js]|s=1,…,n〉是允许理想。对任意正整数s∈{1,…,n-1},ps=[is,js],ps+1=[is+1,js+1]不相交,则kQ/I的整体维数为2。 证明:由定理2.1的证明可知当i∈Q0{ir|r∈N,1≤r≤n}时,mod-kQ/I中单模S(i)的投射维数为1。又当i=ir(r∈N,1≤r≤n)时,有i1 0→P(jr)→P(ir+1)→P(ir)→S(ir)→0, (1)当i (2)当i>j时,记号(i,j)表示长度不大于n的路pi,j=αiαi+1…αj-1。 定义3.1设允许理想I=〈pr=[ir,jr],pt=(it,jt)| 1≤r≤s,s+1≤t≤n〉。 (1)若p,q∈I均包含非平凡子路γ,满足t(p)=t(γ),s(γ)=s(q),则称p,q是相交的。 (2)如果存在m个关系pu,pu+1,…,pu+m-1满足对任意正整数v∈{u,…,u+m-2},pv,pv+1相交且对任意正整数l≠v-1,v,v+1,pv,pl不相交,则称这m个关系有效相交。理想I的有效相交关系数是满足有效相交关系的最大个数,记作N。 (3)设理想I中存在关系pu,pu+1,…,pv是有效相交,其中u 下面给出本节中重要的定理,它揭示了理想与代数整体维数之间的内在联系。 (it,jt)| 1≤r≤s,s+1≤t≤n〉。若I是循环有效相交型允许理想,则g.l.dim(kQ/I)=;否则g.l.dim(kQ/I)=N+1,其中N是理想I的有效相交关系数。 证明:(1) 由已知假设关系pu,pu+1,…,pv是有效相交且关系pv与pu有效相交,其中1≤u (a)若I存在关系pa=[ia,jb],满足ia∈{ju-1,ju+1-1,…,jv-1},此时不妨假设ia=ju-1,则对于mod-kQ/I中的单模S(ia),S(ia)的极小投射分解形如 …→P(ju)→P(jv)→…→P(ju+1)→P(ju)→ P(jv)→…→P(ju+1)→P(ju)→P(jv)→…→ P(ju+1)→P(ju)→P(jb)→P(iu-1)→S(iu-1)→0, 可得p.dim(S(ia))=。 (b)若不存在关系pa=[ia,jb],满足ia∈{ju-1,ju+1-1,…,jv-1}。任取mod-kQ/I中的单模S(ir),r∈N且u≤r≤v,S(ir)的极小投射分解形如 …→P(ju)→P(jv)→…→P(ju+1)→P(ju)→ P(jv)→…→P(ju+1)→P(ju)→P(jv)→…→ P(jr+1)→P(jr)→P(ir+1)→P(ir)→S(ir)→0,可得p.dim(S(ir))=。 (1)允许理想取I=〈[1,5],[2,6],[3,7],[4,8],[6,9],(8,3)〉。 因为理想I是循环有效相交型允许理想,所以g.l.dim(kQ/I)=。 (2)允许理想取I=〈[1,5],[3,7],[5,8],[6,9],(8,3)〉。 因为理想I的有效相交关系数是6,所以g.l.dim(kQ/I)=7。