主轴径向跳动对圆周密封动态特性的影响*
2019-10-23
(1.东北大学机械工程与自动化学院 辽宁沈阳 110819; 2.中国航空发动机集团有限公司航空发动机动力传输重点实验室 辽宁沈阳 110015)
圆周密封是燃气涡轮发动机的关键密封装置之一,其性能直接影响到发动机的性能和使用寿命。发动机圆周密封的功能是保障主轴承腔的滑油密封性能,其属于接触式动密封,要求密封装置具有良好的随动特性[1]。圆周密封中的密封环是由五段石墨组成,在其圆周方向上施加周向弹簧以保证工作中圆周密封环与高速转动主轴时时接触,达到密封性能要求。主轴工作时产生的径向跳动将对圆周密封环产生一个周期性冲击载荷,圆周密封环的动态特性与密封装置的整体性能密切相关,提高圆周密封装置的动态特性对于发动机的工作稳定性、可靠性及使用寿命具有重要意义。因此,对圆周密封装置进行模态分析和谐响应分析,明确其工作中动态特性,可为燃气涡轮发动机圆周密封系统的进一步优化和改进提供基础。作为关键件的石墨密封环受到结构、冲击及热载荷的共同作用,主要的失效形式表现为磨损和脆性断裂[2]。文献[3]通过实验和理论研究了蒸汽旋转接头密封用碳石墨在不同润滑条件下的摩擦磨损性能,得到了磨损量、摩擦力矩和表面温度,探讨了磨损率影响因素的作用规律,并给出了提高密封寿命的设计方案。许多学者研究了石墨复合材料或复合涂层的摩擦磨损性能,分析其磨损机制和失效形式,给出了力学性能数学模型,根据研究结果结合数学方法建立预测模型,为石墨复合材料的应用提供基础[4-7]。KUMAR等[8]研究了卫星运载火箭柔性密封的动态特性,给出了柔性密封的固有频率和前六阶振型,分析了不同垫片材料及垫片数量对固有频率的作用规律。张楠等人[9]研究了石墨接触式密封与涡轮转子系统的振动特性,发现转子弯曲振动和扭转振动随着转速和压紧力的增加而增大,出现了组合共振、零频振动及连续频谱现象,一定转速和压紧力下石墨密封可导致转子的低频振动。YU等[10]利用有限元法对某沟渠装置进行了模态分析和谐响应分析,得到了其固有频率、振型及位移和应力的频响规律。接触式动密封的动态特性对密封性能、使用寿命及可靠性具有很大的影响,研究密封系统的固有频率和相应振型,分析工作中的位移、应力及应变的动态响应规律,对动态密封的设计和优化具有重大的意义[11-13]。
本文作者采用有限元方法,针对某型在役石墨圆周密封进行径向跳动特性和动态特性分析,确定密封环应力和变形随跳动量的变化规律;同时进行圆周密封的模态分析和谐响应分析,为提高石墨圆周密封的随动性能、使用寿命和可靠性提供基础。
1 径向跳动分析
理想状态下密封环工作中受力主要包括径向气体不平衡载荷fcr、轴向气体不平衡载荷fcz、周向弹簧径向力Fsr和波簧轴向力Fsz,密封结构和受力分析如图1所示,各变量计算参见文献[1,14]。文中密封环的径向跳动主要来源于主轴高速转动中产生的周期动不平衡量导致的周期性冲击载荷,周向弹簧径向力保证密封环与主轴时刻保持接触状态,同时,由于密封环的径向跳动,密封环与密封座间产生相对滑动,密封环受摩擦力作用。因此,径向跳动条件下,密封环与主轴接触表面间单位长度接触载荷ftr为
(1)
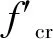
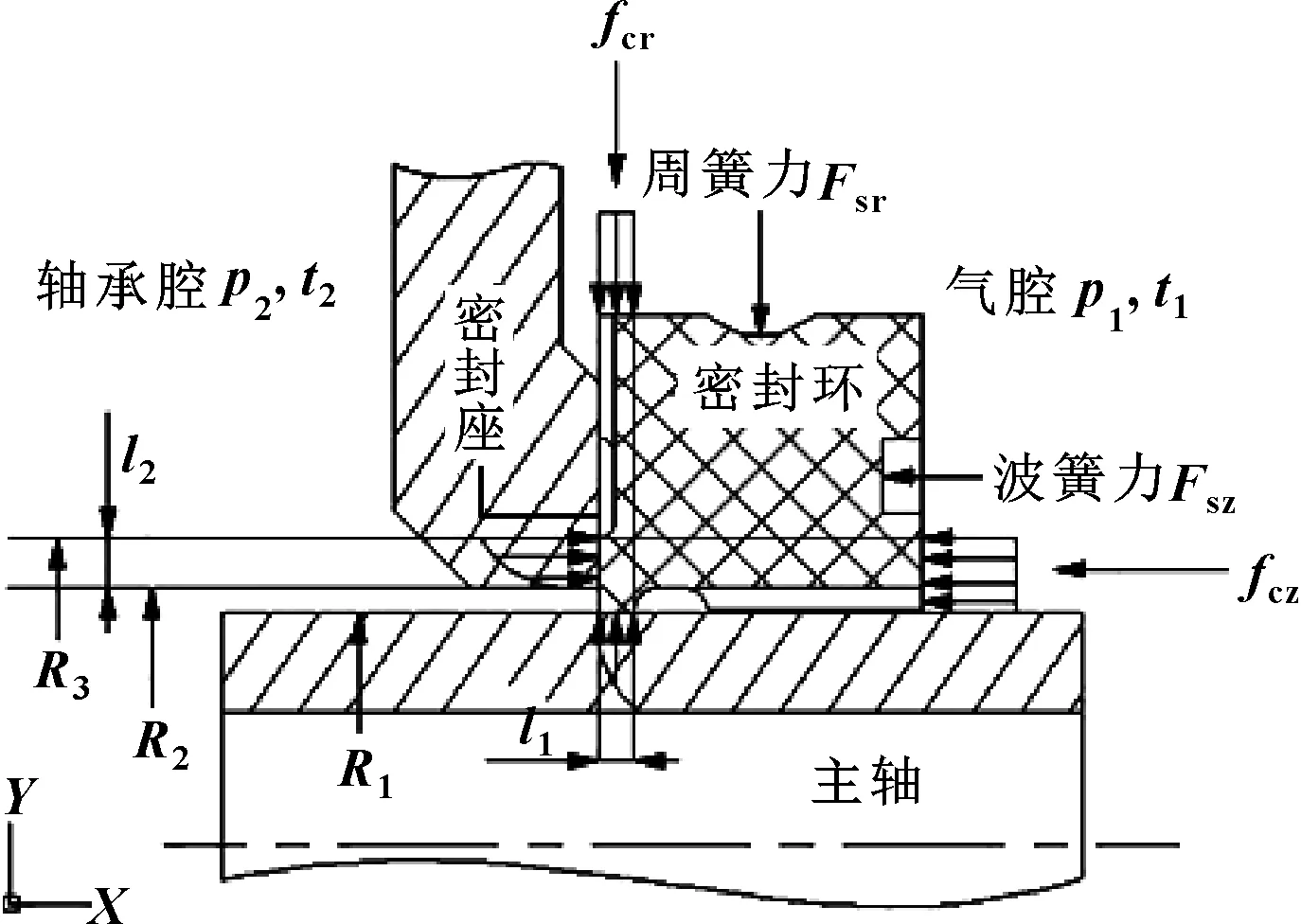
图1 圆周密封环受力分析Fig 1 Force analysis of circumferential seal ring
圆周密封由五段密封环、主轴和密封座及弹簧组成,从受力分析可知各段密封环受力相同,因此分析中选取其中一段密封环段为研究对象,同时考虑到结构对称性和密封环接头结构特点,将主轴和密封座选取1/4,建立有限元分析模型,通过ANSYS Workbench进行分析,结构及分析模型如图2所示。

图2 圆周密封模型Fig 2 Models of circumferential seal (a) structural model;(b)analysis model
密封环与主轴和密封座形成面接触,结构分析采用8节点三维实体SOLID185单元,主、辅助密封面采用8节点高阶四边形CONTA174单元,热分析采用8节点三维实体SOLID70热单元,SOLID70与SOLID185都是8节点单元。网格划分后,模型与结构分析相同,为使模型计算收敛于精确解,对主、辅助密封面进行网格细化。加载和约束:考虑径向跳动的影响,分析中密封环辅助密封面与密封座会沿径向产生滑动,增加了摩擦力,同时径向跳动产生的冲击载荷引起周向弹簧力增加,其他加载和约束方式参见参考文献[14]。
根据在役圆周密封工作条件,研究中径向跳动量分别选取0.2、0.4、0.6、0.8、1.0、1.2、1.4 mm等7个值。图3所示为密封环应力和变形随径向跳动量的变化规律。可以看出,密封环的最大变形量随着跳动量的增大而增大,在跳动量超过0.8 mm后近似呈线性关系,1.4 mm跳动量下的变形量是0.2 mm下的2.7倍;应力随径向跳动量的增大而增大,径向跳动量小于0.6 mm时,增大梯度较小仅为1.5 MPa/mm,而当跳动量大于0.8 mm后,最大应力值增大梯度显著增加达到了3.3 MPa/mm,最大应力也达到了5.066 MPa,但仍小于密封环材料许用应力,就结构强度而言,密封环还可以承受更大径向跳动量。分析认为:随着跳动量的增加,作用于密封环上的冲击载荷增大,但为了满足密封的随动性要求,周向弹簧力随之增大。同时,由于径向跳动导致的密封环辅助密封面与密封座间产生动态滑动摩擦,对密封环产生一定的摩擦力,并导致密封环磨损,这样轴向弹簧的作用力也要增大以满足密封性能要求。分析结果为进一步提高考虑径向跳动的圆周密封性能和使用寿命提供了设计基础。

图3 应力和变形与径向跳动量关系Fig 3 Stress and deformation vs. radial runout
2 动态特性分析
2.1 模态分析
径向跳动对密封环产生一个周期性冲击作用,这种冲击载荷的存在对密封环随动特性、密封性能及周向弹簧使用寿命等产生极大影响,因此,在考虑存在径向跳动的工作条件下,对于与高速旋转主轴配合密封环进行动力学特性研究非常必要。
多自由度结构系统的动力学方程[15]可表示为
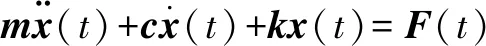
(2)
式中:m、c、k分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;F(t)为激励矢量;x(t)为位移矢量。
振动模态是圆周密封环的固有特性,由结构本身属性决定,与外载荷无关。阻尼对其固有频率和振型影响较小,无外载荷和忽略阻尼动力学方程可表示为
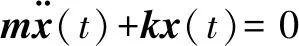
(3)
圆周密封系统作简谐振动,则有
x(t)=φsin(ωt+α)
(4)
式中:φ为特征矢量或振型;ω为角频率;α为初始相位角。
则式(3)可表示为
(k-ω2m)φ=0
(5)
为求得非零解,须满足det(k-ω2m)φ=0,此即为振动模态的特征值方程,特征值ωi即为结构的n个固有频率,φi即为振动频率下振动型态。
密封环采用10节点四面体SOLID187单元,主轴和密封座采用20节点六面体SOLID186单元,分析模型划分后共有164 955个节点,92 024个单元。根据圆周密封的工况,密封座采用全固定约束,主轴只有周向回转,密封环周向和轴向施加弹性约束,密封环防转销处施加微动位移约束。
由振动理论可知,低阶模态对结构振动贡献大,而高阶振动对响应影响较小,且高阶振动响应衰减很快[15]。同时,根据所分析的在役圆周密封的工作条件,只对密封环前6阶模态进行分析。密封环前6阶固有频率如表1所示。

表1 固有频率Table 1 Natural frequency
图4示出了密封环前6阶模态振型。可以看出,1阶模态振型在密封环周向(Y轴方向)表现为局部摆动,摆动引起的变形在密封环中部大,密封环端接头处小(如图4(a)所示);2阶模态振型出现了沿密封环径向方向(X轴方向)的弯曲振动,变形量增大且位于密封环端部(如图4(b)所示);3阶模态振型密封环表现为径向(X轴方向)较强的弯曲振动,较大的变形位于密封环中部,同时出现了轴向(Z轴方向)弯曲振动(如图4(c)所示);4阶模态振型表现为密封环在径向(X轴方向)和轴向(Z轴方向)由弯曲振动转化为扭转振动(如图4(d)所示);5阶模态振型在密封环径向(X轴方向)上出现较弱的振动,轴向(Z轴方向)上存在局部摆动现象(如图4(e)所示);6阶模态振型密封环在XY和YZ平面内均出现了强烈的扭转振动,比4阶模态振动更加复杂(如图4(f)所示)。模态振动在XOY平面内的X向和Y向引起的变形对圆周密封环周向弹簧的疲劳寿命产生影响,同时,加剧了防转销与销槽间的微动磨损,模态振动在密封环轴向(Z向)产生扭转振动引起的变形对密封环轴向的波簧的疲劳寿命产生影响,并将改变辅助密封面与密封座间的磨损性能,从而影响圆周密封的随动特性、密封性能及使用寿命。
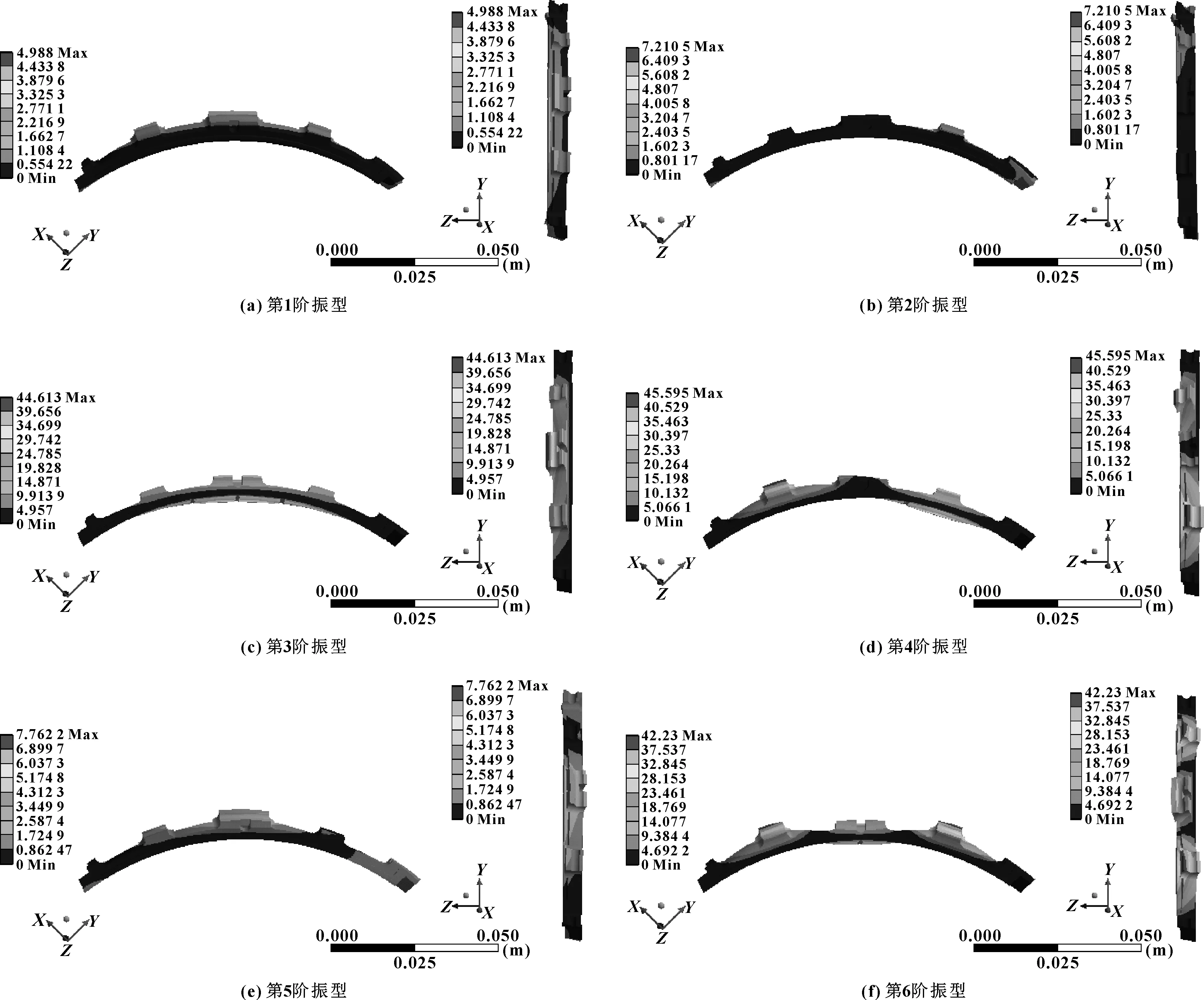
图4 圆周密封环前6阶振型Fig 4 The first six modal shape of circumferential sealing ring(a) first order vibration model;(b) second order vibration model;(c) third order vibration model;(d) third order vibration model;(e) fifth order vibration model;(f)sixth order vibration model
2.2 谐响应分析
谐响应分析是为了确定结构持续动力特性,使圆周密封环工作中避免由于强迫振动而引起的共振现象。圆周密封环在承受冲击载荷作用下受迫振动运动微分方程[16-17]为
(6)
式中:F0sin(ωt)为强迫简谐振动。
若节点位移响应为
x(t)=Asin(ωt+θ)
(7)
式中:A为幅值;θ为响应滞后激励载荷相位角。
将公式(7)代入公式(6)则有
(8)
给定ω的频率范围和频率间隔,分析可得到位移与频率的关系,从而得到曲线的峰值频率,而后根据峰值频率求得应力值。
为了得到周期性冲击载荷下密封环响应特性,对密封环进行谐响应分析,并结合模态分析结果为圆周密封的设计分析提供基础,避免共振危害发生。通过ANSYS分析软件对圆周密封进行谐响应分析,网格划分及边界条件施加与模态分析方式相同。基于模态分析结果,谐响应分析扫描频率范围为2 000~11 000 Hz,扫频间隔30 Hz。针对圆周密封性能的特性,谐响应分析中主要考虑密封环由于周期冲击载荷作用引起的X向和Y向变化规律。
图5所示为圆周密封环在X向和Y向上应力和位移的频率响应曲线。由图5(a)可知,当扫描频率达到2 200~2 400 Hz时,圆周密封环在X向和Y向的应力出现较小的波动,而后表现为一段频率范围的小幅渐增趋势;当扫描频率达到6 770 Hz时,应力值为0.105 MPa(X向)和0.168 MPa(Y向),Y向的应力值为X向的1.6倍;扫描频率为8 570 Hz时;X向的应力达到最大值0.360 MPa,Y向的应力也出现了较大值0.137 MPa,但Y向的应力值仅为X向的38%;扫描频率达到9 230 Hz时,X向和Y向又出现了较大的应力值,但较频率为6 770和8 570 Hz时的应力值小;扫描频率达到10 040 Hz时,在X向和Y向再次出现了大的应力值。出现较大响应力的频率点,X向的变化为先增大再减小的变化规律,而对于Y向则表现为逐渐减小的变化趋势。从图5(b)可以看出,圆周密封环位移在2 200~2 400 Hz频率之间出现小幅波动,在频率达到6 770 Hz时,出现了极大的位移值,X向位移值为6.39×10-3mm,Y向位移值为0.49×10-3mm,仅为X向的8%;扫描频率达到8 570 Hz时,X向位移值达到了扫描频率范围内的最大值9.35×10-3mm,Y向位移值也达到了扫描频率范围内的最大值0.94×10-3mm,是6 770 Hz频率下的1.9倍;当扫描频率达到10 040 Hz时,X向位移再次出现较大值,但比6 770和8 570 Hz频率下的要小,仅为最大位移值的7.5%。在扫描频率范围内,X向在几个频率点上的响应位移均大于Y向响应位移。圆周密封环应力和位移响应出现大幅值响应频率分别为6 770、8 570和10 040 Hz,结合模态分析结果可知,6 770 Hz对应于圆周密封环的3阶固有频率,8 570 Hz对应于圆周密封环的4阶固有频率,10 040 Hz与密封环的6阶固有频率相近。因此,分析条件下在役圆周密封第3阶和第4阶模态下可能出现共振问题,对于第6阶模态下的共振也要给予足够的重视,共振的出现除危害圆周密封,同时对于周向弹簧的疲劳寿命及防转销钉处的微动磨损和疲劳寿命也将产生极大的影响。
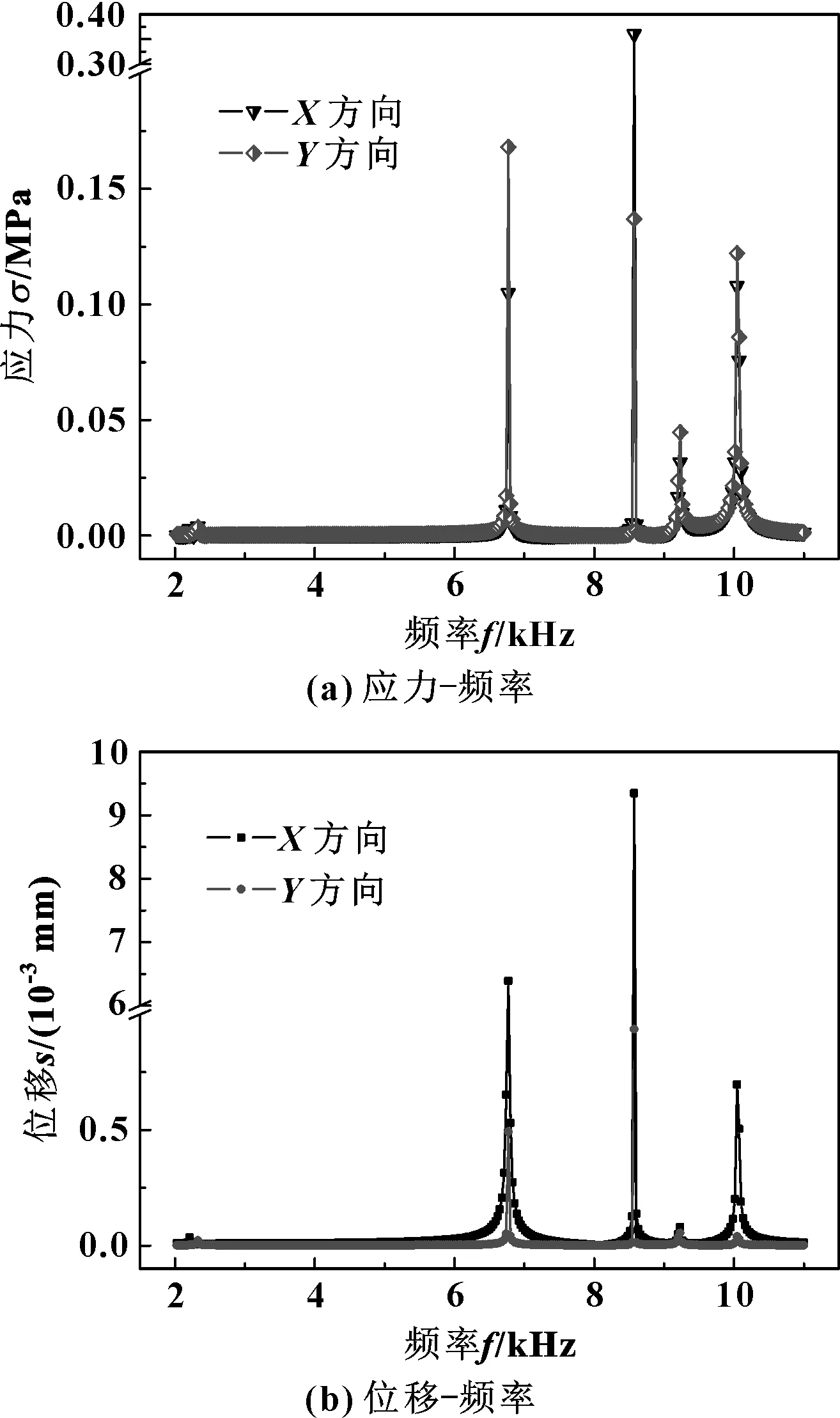
图5 频率响应曲线Fig 5 Frequency response curves (a)stress vs frequency;(b)displacement vs frequency
3 结论
(1)建立了考虑径向跳动条件下的密封环所受到的接触载荷计算公式,得到了石墨圆周密封热-结构耦合条件下的应力和变形与跳动量间的变化规律。结果表明:应力随径向跳动量增大而增大,跳动量超过0.8 mm后,应力增大梯度显著变大;最大变形量随径向跳动量增加而增加,跳动量超过0.8 mm后近似呈线性关系。
(2)得到了石墨圆周密封环前6阶固有频率和振型,模态振动对周向弹簧和轴向弹簧疲劳寿命具有较大的影响,加剧防转销与销槽间微动磨损,从而影响圆周密封的随动特性、密封性能及使用寿命。
(3)通过模态分析和谐响应分析,在役圆周密封在3阶和4阶模态下可能出现共振现象,6阶时也存在一定共振问题,改进设计中应该重点关注。
