基于声学黑洞的压电俘能结构系统仿真与优化

汪 恒,郑伟光，何仕明，陈姗姗

(桂林电子科技大学 机电工程学院, 广西 桂林 541004)

0 引言

随着各种无线设备自供能的需求，从环境中采集振动能量成为国内外学者研究的热门方向[1]。由于振动产生的能量分散，大小不一，如何有效集中采集环境中的振动能成为研究的关键。1988年，Mironov[2]提出的一种用来实现对弯曲波振动控制的“声学黑洞(ABH)”效应，通过结构阻抗的变化，使得结构中波的相速度发生变化，在结构特定区域实现波的能量聚集[3]。声学黑洞将物理学中的黑洞概念引入到声振领域，并在振动与噪声控制及能量收集领域得到广泛的关注[4-7]。在压电材料与声学黑洞结合方面，Remillieux等[8]将压电分流阻尼技术引入声学黑洞结构，通过采用负电容电路，实现了全频段振动控制；Zhao等[9]采用有限元法对压电俘能结构进行了频域稳态分析及时域瞬态分析，结果表明，与均质板结构相比，压电俘能结构具有声学黑洞结构的压电换能器在宽频范围内有更高能量转化效率。

目前，很少有学者对具有声学黑洞结构的压电俘能系统建立系统电路仿真及负载电阻优化进行研究。本文首先采用有限元法建立具有声学黑洞的薄板结构压电耦合模型，对比分析了均匀板及声学黑洞结构的动能密度及电压瞬态输出特性，推导了压电振子等效电路模型，最后在Multisim软件中建立压电俘能全系统等效电路耦合模型，确定外负载最优电阻值，提高系统转换效率。

1 声学黑洞结构

在一维结构变化的均匀介质中，弯曲波动方程为

(1)

式中：w为结构横向位移;D=Eh3/[12(1-ν2)]为弯曲刚度，E为杨氏模量，ν为泊松比；ρ为密度；h为结构厚度；t为时间变量。

对任意一点，x波传播的振幅可表达为复数形式，即

U(x)=A(x)eiΦ(x)

(2)

其中：

(3)

(4)

式中：Φ为累积相位;kp=ω/cp为均匀板的波数。

对于一个厚度呈现指数形式变化的结构为

h(x)=εxm

(5)

其弯曲方程为

(6)

假设不考虑结构的转动惯量与剪切效应，波数k为

(7)

式中ω为角频率。根据c=ω/k可得弯曲波的相速度为

(8)

将薄板按照一定指数进行裁剪，使其厚度变化满足h(r)=εr2(m≥2),即可形成声学黑洞。在二维声学黑洞中随着厚度的减小，弯曲波的相速度也逐渐减小产生能量聚集效应。当指数m≥2，Φ区域将无限大，波无法到达边界也无法反射回来，因此弯曲波在边缘产生聚集。

2 声学黑洞型压电俘能器结构

实际薄结构中的厚度不会减小至0，黑洞结构中心存在截断。本研究在声学黑洞薄板中心留有一厚度L、半径r0的圆形平台，黑洞结构的幂指数变化为h(r)=5×10-4×r2,(r0≤r≤100),结构其他均匀处厚度不变。在板结构的左边界进行约束，距离固定端边界L1处的均匀板面上施加点载荷F=Asin(2πft),以距离固定边界L2处的薄板黑洞结构中心下表层粘贴半径r0、厚l3的陶瓷压电片PZT-5H。

3 有限元分析

3.1 参数设置

本研究的薄板材料选用铝板，压电片材料选用PZT-5H，结构尺寸及材料参数如表1所示。假设基体部分与压电层为理想粘结，进行良好的结构应变传递。

表1 结构尺寸及材料参数

3.2 仿真分析

通过有限元软件在0～1 ms时间段进行仿真，每隔0.05 ms选取薄板在应力云图(见图1、2)及动能密度图(见图3)的周期性变化。

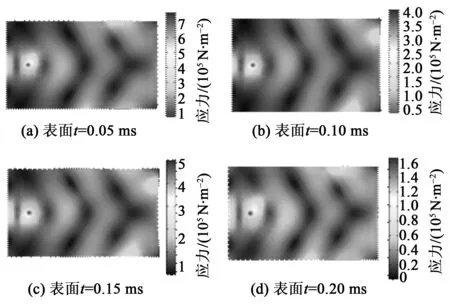
图1 均匀薄板的应力云图

图2 黑洞结构薄板应力云图

图3 薄板动能密度对比图

在建好的模型中分别在两块薄板上选取固定位置，其三维坐标为(75,130,5)，施加幅值为3 N的正弦激励。由图1～3可看出，声学黑洞结构薄板在黑洞中心部分有较大的能量聚集效应。选取薄板中心的固定位置(225,130,0)进行动能密度比较，均匀板上动能密度峰值为0.017 4 J/m3，而声学黑洞结构板的能量密度峰值为0.652 J/m3，从图3可发现，在0～1 ms时均匀板和黑洞结构的薄板动能密度呈现周期性变化，具有声学黑洞的动能密度明显高于均匀板的能量密度。可见，在点载荷的激励下弯曲波进入黑洞结构区域后波长压缩，波动幅度增大，振动能量在结构中心进行累积，形成声学黑洞结构薄板所示的能量集中，图1～3给出了具体验证。

3.3 压电俘能器输出电压分析

在两块不同结构的薄板表面特定位置粘贴陶瓷压电片，在不考虑电阻值、压电片形状大小等其他变量的影响下，进行有限元软件的多物理场耦合仿真，两块薄板的输出电压图如图4所示。

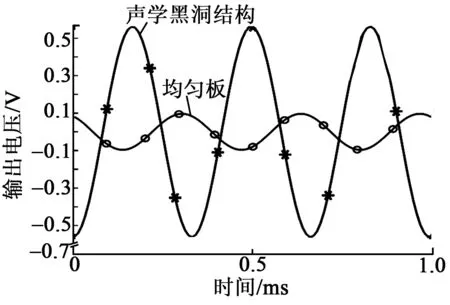
图4 时域下不同模型的输出电压

在相同位置给2块薄板施加同样的激励，在0～1 ms内对其输出电压进行分析发现，2块薄板结构输出的电压同样呈周期性变化，选取2块板的输出电压峰值点，均匀板输出的最大电压为0.096 V，声学黑洞结构薄板输出电压峰值达到0.562 V。通过对比，声学黑洞结构薄板的压电振子输出电压较均匀板提高了近6倍。

4 压电俘能器全系统耦合

本文通过对压电振子的结构进行设计，提高了压电振子的电压输出效果，进而提高系统的俘能效率。但实际应用中，压电俘能器是由压电振子结构和能量俘获接口电路共同发挥作用。由于压电片存在逆压电效应，外部电路会对结构的振动响应和动力学特性产生影响，同时，压电振子输出的交流电压对电路中转化的直流电压产生影响。因此，本研究为了提高压电俘能器的全系统效率，将压电振动能量俘获系统看成一个整体进行优化设计，建立压电振子等效电路模型和压电俘能全系统等效电路耦合模型[10]。

4.1 压电振子等效电路模型

耦合建模中常用的理念方法是通过机械量与电路参数的转化来表征压电振动产生的能量。如图5所示，分别将均匀板和具有声学黑洞结构的新型压电振子模型机械参数进行等效电路模型转化。

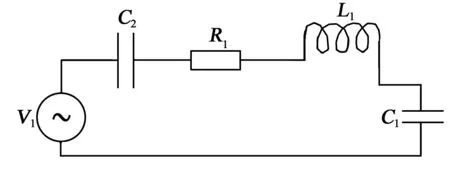
图5 压电振子等效电路图

求解等效电路模型中的参数V1、R1、C1、L1、C2是本研究的关键。目前有理论推导、实验检测和有限元仿真3种方式。理论推导方法要求几何形状规整，实验测量方法复杂，过程要求高，且有些参数不能直接测量得出。鉴于前面两种方式的局限性，本研究采用有限元仿真法能有效适用于几何形状不规律的压电振子模型，且能快速准确计算出等效电路参数。

利用现有的压电振子模型，通过Comsol软件对其进行短路共振频率f(C1)、开路共振频率f(C2)、电荷Q0、短路电压V(C1)、开路电压V(C2)仿真计算。

1) 压电振子短路条件下的共振频率。在仿真软件中将压电振子的输出端电路短路。在Comsol中进行特征值分析，可得出短路共振频率f(C1)，且

(9)

2) 压电振子开路条件下的共振频率。在仿真软件中将压电振子的输出端不接任何负载构成开路。在Comsol中进行特征值分析，可得出开路共振频率f(C2)，且

(10)

3) 在上述模型中，将压电振子在输出端不接任何负载构成开路，在压电振子2个电极上施加直流电压V0,计算产生的Q0，即

Q0=(C1+C2)V0

(11)

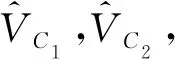
(12)

(13)

由式(9)～(11)可计算C1、L1、C2。由式(12)、(13)可得：

(14)

(15)

由(14)、(15)可计算出V1、R1。

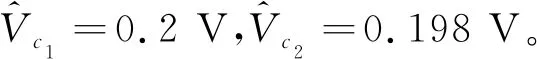
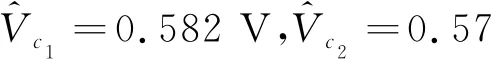
最后根据式(9)～(15)得出压电振子等效电路模型，如表2、3所示。

表2 均匀板压电振子等效电路参数估计值

表3 黑洞结构薄板压电振子等效电路参数估计值

4.2 基于Multisim的全耦合等效电路

压电振子在振动产生电能的过程中，外部电路负载的大小会影响压电振子和电路的耦合，进而影响压电俘能器整体的效果。本研究通过在Multisim建立外接全桥整流电路的振动俘能等效电路模型，重点分析压电俘能系统外负载电阻对能量转换率的影响，取0≤R2≤10 000 Ω，确定负载的最优取值范围。图6为压电振子俘能系统等效电路图。

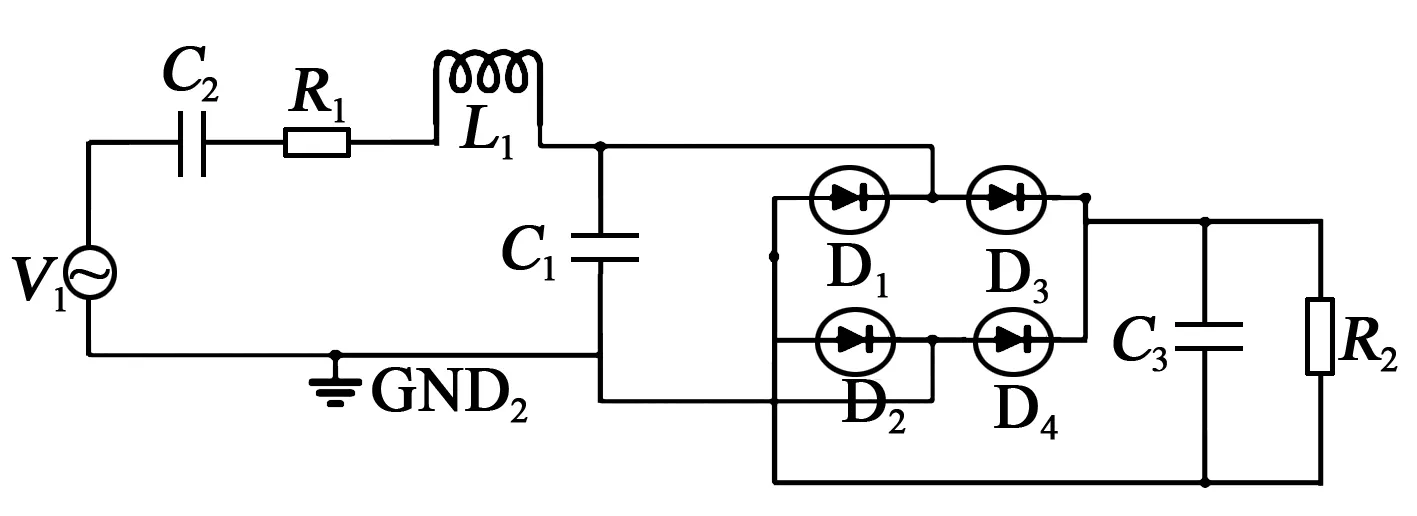
图6 压电振子俘能系统等效电路图

在外接全桥整流电路，通过仿真可得上述两种压电俘能装置的俘获功率与负载电阻值的关系，如图7所示。

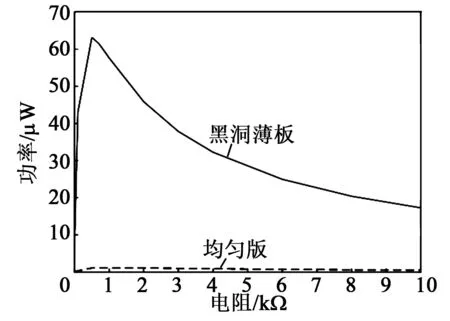
图7 系统俘能功率与外负载的关系

由图7可看出，在进行均匀板等效电路仿真时，当外部电阻R2≈1 500 Ω，系统的最优俘能效率可达1.093 μW；在进行声学黑洞结构薄板等效电路仿真时,当外部电阻R2≈510 Ω，系统的最优俘能效率可达63.098 μW，声学黑洞结构薄板的压电俘能装置系统的转换效率较均匀板压电俘能装置有显著提高。

5 结束语

本文将声学黑洞结构引入到压电俘能器中，通过理论及仿真分析了弯曲波在黑洞结构中聚能效果。在时域上对比分别研究了两类俘能装置的表面应力云图、动能密度图及输出电压图。结果表明，具有声学黑洞结构的新型压电俘能器能够有效提高薄板的振动能量收集和压电能量的转换。同时，利用新型压电俘能器建立全系统等效耦合电路模型，进行电路仿真分析，确定外负载电阻的最优取值范围，提高系统能量的转换效率。本研究的声学黑洞结构俘能装置结构简单，造价低，聚能效果好。结合目前微电子器件和传感器的自供能需求，声学黑洞结构俘能器在实际工程应用中具有极大的实用价值。