众包竞赛的离群点欺诈用户检测算法研究

许艳静，朱建明，丁庆洋，庄雪扬

(中央财经大学 信息学院，北京 100081)

一、引言

众包竞赛(Crowdsourcing Competition)由于能够充分发掘社会大众的智慧而被企业广泛应用。众包竞赛指企业通过第三方网络平台举办一些创新竞赛，向来自世界各地参与竞赛的社会大众征集任务解答方案，并给予一定现金奖励的新模式[1]。在众包竞赛中，欺诈问题时有发生，这种行为降低了创新效率，引起了众多学者的广泛关注。庞建刚通过博弈分析指出，由于交易双方的信息不对称，欺诈行为容易产生，且发起者是风险重要来源[2]。冯剑红等发现，问题解答者的欺诈行为已经严重影响任务的完成质量，如何识别出欺骗型解答者成为目前众包研究中一个急需解决的问题[3]。平台运营商和发起者是众包竞赛中筛除欺诈者的行为方。从网络平台角度看，常见的方式是利用黄金标准数据和测试题目。黄金标准数据方法是把解答者的数据和标准答案对比，筛选出欺骗类的解答者，并舍弃他们的答案。这种方法如果没有清晰标准的答案便失去了可行性。也可以通过添加一些测试题目筛选出一些欺诈者[4]，但是很多解答者并不想参加测试，导致题目不能长时间被完成。从任务的发起者视角看，筛除欺诈者可以依靠在题目中随机添加一部分常识问题，如若这些问题回答错误，便可剔除欺诈者，这样既提高结果质量又可以避免浪费金钱。但是，这种方法有个很大的挑战，就是如何做到隐蔽地插入常识。

离群数据是指数据集中那些远离常规对象的数据，表现为与多数常规对象有明显差异，以至于被怀疑可能是由另外一种完全不同的机制产生[5]。众包中欺诈用户的个人信息和历史记录信息及参与众包工作的答案和大众信息相比是有很多的区别的，均可以利用一些新的方法从大众中作为离群点分离出来。因此，离群点检测是优化欺诈者筛除机制的关键所在。

离群点检测是识别数据中噪音，挖掘潜在的、有意义的知识的一种数据挖掘技术[6]，广泛应用于入侵检测领域、信用卡诈骗检测、电子商务犯罪活动检测、视频监控、天气预测以及药物研究等研究中。由于聚类算法能够根据样本之间的相似度把观测样本分到不同分组，并使同一分组中的样本尽可能相似而不同分组中的样本尽可能不相似，因此聚类算法被用于识别数据中的离群点。

离群点的检测方法有很多，常见的有基于距离的和基于密度、基于分布的、基于深度的、基于方法的几大类。为了消除离群点对聚类的影响，提出了能够识别样本聚类和离群点的ORC(Outlier Removal Clustering)算法[7]，该算法先是用K-means-聚类算法对样本聚类；然后根据样本点与聚类中心之间的距离来判断哪些点是离群点并移除。在给定样本间平均距离的情况下，ODC(Outlier Detection Clustering)算法将大于样本间平均距离p倍的点视为离群点[8]。K-means-算法能够同时识别聚类和离群点，该算法需要给定聚类个数k和离群点个数l。在给定参数的情况下，K-means-算法每次迭代会计算样本点与最近的聚类中心的相似度，并按大小进行排序，将距离最大的前l个点视为离群点，用剩下的样本点来重新计算聚类中心，直到满足终止条件[9]。

二、众包竞赛的离群点欺诈用户检测算法的设计

(一)众包的组织框架

我们将众包工作概念化[10-12]。监测和评估人群行为; 验证用户的身份，然后才能在网站上发布信息或参加在线竞赛; 删除虚假信息;筛选用户有可能标记可疑内容或者虚假答案。

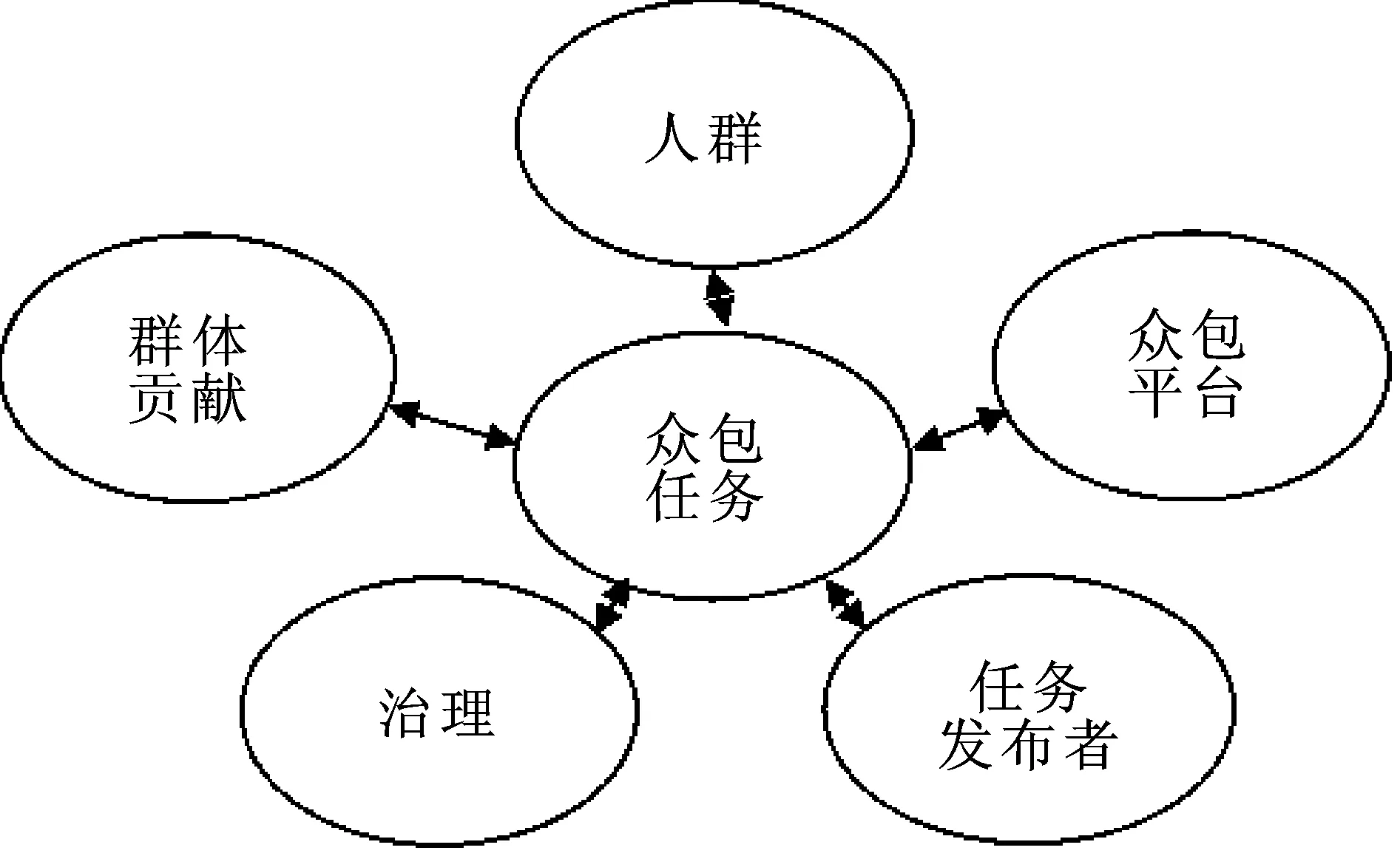
图1 众包工作概念框架

我们的众包工作概念模型包括以下要素(图1)：

(1)众包任务：众包任务也被称为问题或挑战。

(2)人群：执行任务的个人(人群工作人员)。在欺骗性众包的背景下，与人群相关的问题涉及恶意的人类行为，以及可能引发此类行为的机制的识别。

(3)众包平台：连接人群和问题所有者。在捕捉众包欺骗的例子时，我们将重点放在与平台或其管理相关的风险和漏洞上。

(4)任务发布者：定义任务，在平台上发布任务，并为任务完成提供数据和工具。对于我们的分析，我们集中于与问题所有者的上下文相关的有关风险的信息，这些风险是由任务发布者发起的，或者是由他们的疏忽引起的。

(5)治理/管理：我们收集了关于事件中使用的治理机制和相关漏洞的信息，例如缺乏质量控制，使用离群点检测方法。

(6)群体贡献：人群成员完成任务后的产出。

(二)离群点的定义

众包框架中治理模块的内容涵盖了众包的用户的管理，众包的欺诈用户检测管理我们可以利用检测离群点的方式操作。离群点是指数据中偏离大多数样本的样本集合，聚类分析中的离群点则定义为远离聚类中心的样本集合[13]。应用在众包中我们可以给定n个观测样本的集合Xi=(X1，X2，…，Xn)T，假设Ck是聚类中心集合，用d(Xi，Ck)来表示样本Xi与聚类中心Ck之间的相似度或距离。给定参数θ，用f(θ)来检测样本是否为离群点，若d(Xi，Ck)>f(θ)，则样本Xi是远离聚类Ck的离群点，反之若d(Xi，Ck)≤f(θ)，则样本Xi不是聚类Ck的离群点。

(三)离群点检测算法

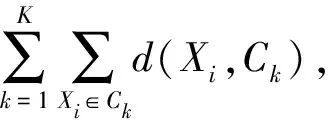
(四)基于样本连通图的离群点检测算法

由于基于聚类算法的离群点检测算法K-means-算法[15]和DBSCAN算法[16]依赖于事先给定的参数，因此要提升算法的准确性，必须准确设置参数，在实践中要准确设置参数往往是困难的。为此，本文提出了基于样本连通图的离群点检测算法(Outlier Detecting Algorithm Based on Sample Connection Graph，简称为ODA-SCG)。

1.相关定义。给定参数θ，利用聚类算法来识别数据中的离群点并对数据进行聚类，将会得到不同的聚类结果和离群点集合：{Xs，Xo}，其中Xs={C1，C2，…，Ck}。对于任意两个样本点Xi和Xj，若它们都属于第k个聚类或都是离群点，即Xi，Xj∈Ck或Xi，Xj∈Xo那么认为这两个样本之间存在连接关系Eij=1。若Xi和Xj不属于同一聚类或者不都是离群点，那么它们之间没有连接Eij≠1。随着参数θ取值的不断变化，聚类结果会发生变化，样本Xi和Xj之间的连接情况也会发生变化。因此，在给定不同参数θ的情况下，Xi和Xj之间的连接情况是一个随机变量。

定义1连接强度。用X表示包含n个观测样本的集合，假设Xi和Xj是来自数据集X的两个样本点，用Eij表示Xi与Xj之间是否连接，Eij=1表示有连接，Eij=0表示无连接。用Xi与Xj之间连接的概率p(Eij=1)∈[0，1]来表示连接强度，简记为pij。

接下来讨论如何估计两样本之间的连接强度pij。由于K-means-算法和DBSCAN算法识别离群点时，依赖于设定的参数值，那么给定不同的参数值，得到的聚类结果和离群点识别结果将会有所不同。为了解决这一问题，我们给定参数范围，然后利用K-means-算法和DBSCAN算法重复识别离群点，然后通过两个点被划分到同一个类别的频率，来估计Xi与Xj之间的连接强度。

定义 2连接强度计算。对于任意两个样本点Xi与Xj，若它们同属于一个聚类或都是离群点，则它们之间有连接Eij=1。给定参数范围，重复调用离群点识别算法来识别离群点N次，计算任意两个样本Xi与Xj被分配到同一个聚类或都是离群点的总次数为#(Eij=1)。那么定义连接强度pij为：

pij=#(Eij=1)/N

可见，当且仅当任意两个样本点Xi与Xj同属一个聚类或者都是离群点时，它们之间有强的连接强度，否则它们的连接强度较弱。

定义3样本连通图。定义样本连接图G(X，E，p)，其中X是样本节点集合，E是样本节点之间的连边集合，p是样本节点之间的连接强度集合。为了使样本之间的连通图变得稀疏，定义样本之间的连接强度下界δ∈[0，1]，用来限制两个样本之间的连接情况。当且仅当pij>δ时，样本节点i与样本节点j之间有连接，否则无连接。

2.算法设计。根据上述定义，下面给出基于样本连通图的ODA-SCG，用来识别数据中的离群点。基于样本连通图的离群点检测算法(ODA-SCG)的实现，主要完成以下方面的工作：

(1)观测样本集合X，连接强度下界δ，离群点识别算法参数范围；

(2)给定聚类个数和离群点个数，通过K-means-聚类算法初始化聚类中心C；

(3)循环迭代直至满足收敛条件；

(4)计算各观测样本与其最近的聚类中心的距离d(Xi；Ck)，并由大到小排序；

(5)将前l个距离聚类中心最远的观测样本从聚类中剔除，得到余下观测样本集合Z；

(6)利用余下观测样本集合Z重新计算聚类中心；

(7)输出聚类分析结果和离群点集合；

(8)将观测样本集合X中的所有样本点标记为未处理状态；

(9)循环迭代直至每个样本被归入某个聚类或标记为离群点；

(10)统计样本点Xi的eps邻域内包含的样本点数Neps(Xi)；

(11)如果Neps(Xi)包含的样本数小于Minpts，则将Xi标记为边界点或离群点；

(12)否则标记Xi为核心对象，并建立新聚类C，将Xi的eps邻域内的样本点划分至聚类C中；

(13)循环迭代直至Neps(Xi)中所有尚未被处理的对象Xj被归入某个聚类或标记为离群点；

(14)统计样本点Xj的eps邻域内包含的样本点数Neps(Xj)；

(15)如果Neps(Xj)包含至少Minpts个样本点，则将Neps(Xj)中未归入任何簇的对象加入C；

(16)输出聚类划分和离群点集合；

(17)计算连接次数#(Eij=1)和连接强度pij；

(18)给定连接强度下界δ，构造样本之间的联通图；

(19)判别样本在连通图中的位置，标记离群点；

(20)输出离群点集合，算法实现流程见图2。

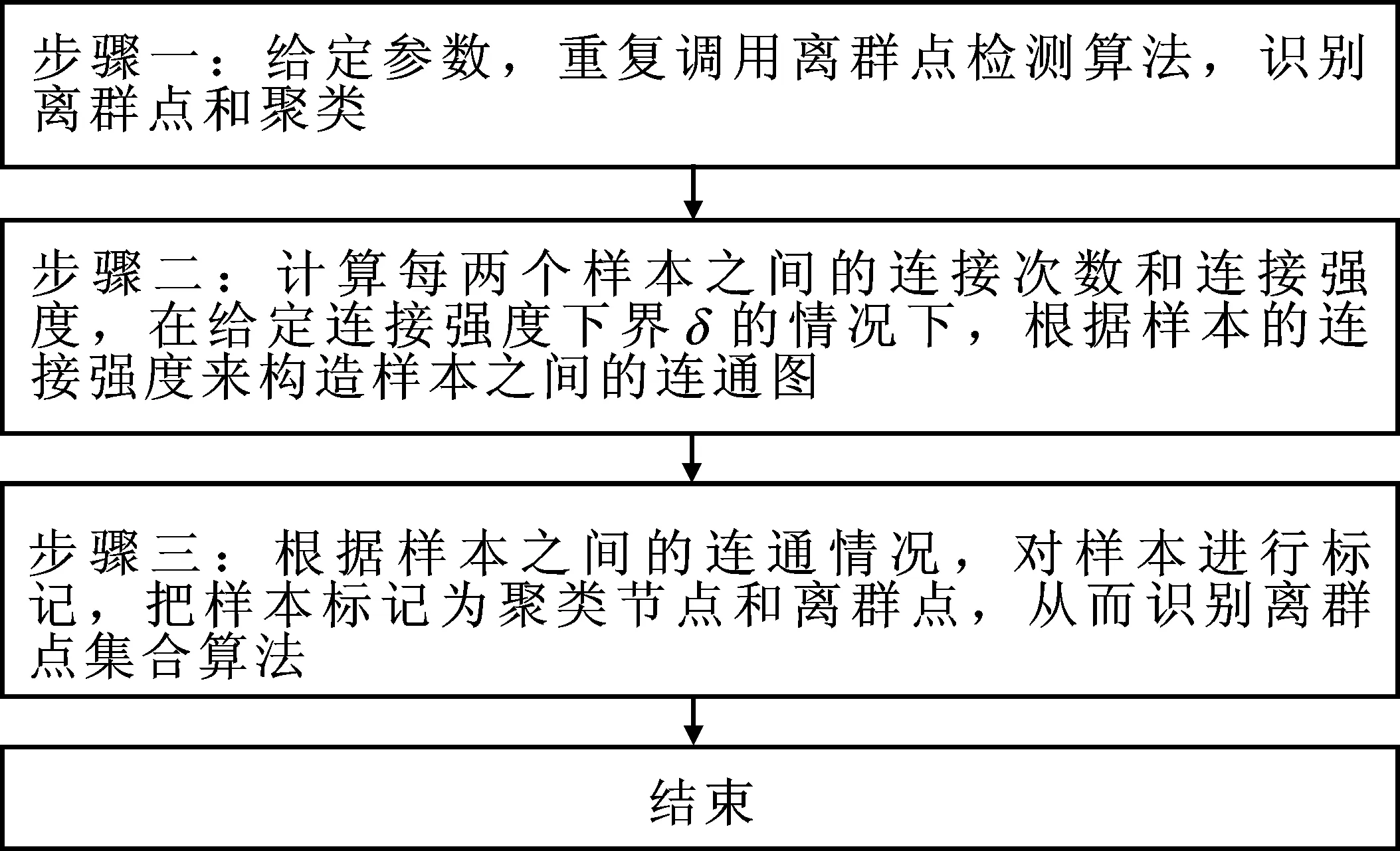
图2 基于样本节点连通图的离群点检测算法流程

算法与K-means-离群点检测算法和DBSCAN离群点检测算法相比，它给定的参数是一个范围，且通过重复调用离群点检测算法并计算样本节点之间的连接强度。这样就避免了参数设置不准确时，离群点检测结果与实际结果偏差较大的问题，解决了基于聚类的离群点识别算法过度依赖于给定参数的问题，离群点的识别结果较为稳定。

以K-means-离群点检测算法为例，它需要确定聚类个数K。为了确定聚类个数，本文通过最优化聚类内部有效性指标KL来确定最佳的聚类个数[17]。

三、实验环境

本实验采用R3.4.1软件作为实验平台，操作系统是Windows10专业版，Intel(R) Core(Lawrence et al.) i7-7560U CPU @2.40GHz(双核)64位，16GB内存，512GB固态硬盘。

(一)评价方法

为了评价ODA-SCG算法的有效性，本文采用离群点个数(Number of outliers，简写为No)、灵敏度(Sensitivity，简写为Sen)、特异度(Specificity，简写为Spc)、准确率(Accuracy，简写为Accu)以及F-measure(简写为F)作为评价指标。其中灵敏度、特异度、准确率以及F的取值范围在0和1之间，数值越接近1，说明算法准确度越高，反之算法准确度越低。

将非离群点表示为正类，离群点表示为负类，用TP表示判别为正类且实际为正类的样本点个数，FN表示判别为负类但实际为正类的样本点个数，TN表示判别为负类且实际为负类的样本点个数，FP表示判别为正类但实际为负类的样本点个数。因此，Sen、Spe、Accu和F的定义如下：

Sensitivity =TP/(TP+FN )

Specificity=TN/(TN+FP )

Accuracy=(TP+TN )/(TP+TN+FP+FN )

F-measure=2(Precision·Recall)/(Precision+Recall)

其中，Precision为精度，其计算公式为TP/(TP+ FP )；Recall为召回率，其计算公式为TP/(TP+ FN )。

(二)实验数据

为了测试算法的准确性，本文借助R软件生成仿真数据集。仿真数据的产生有三种情形：聚类之间完全分离，聚类大小不同以及聚类密度不相等。同时，设置两种不同的离群点比例情形：离群点较少(5%的样本点为离群点)和离群点较多(20%的样本点为离群点)。因此，共有六种数据集将用来验证离群点检测算法。具体设置见表1。

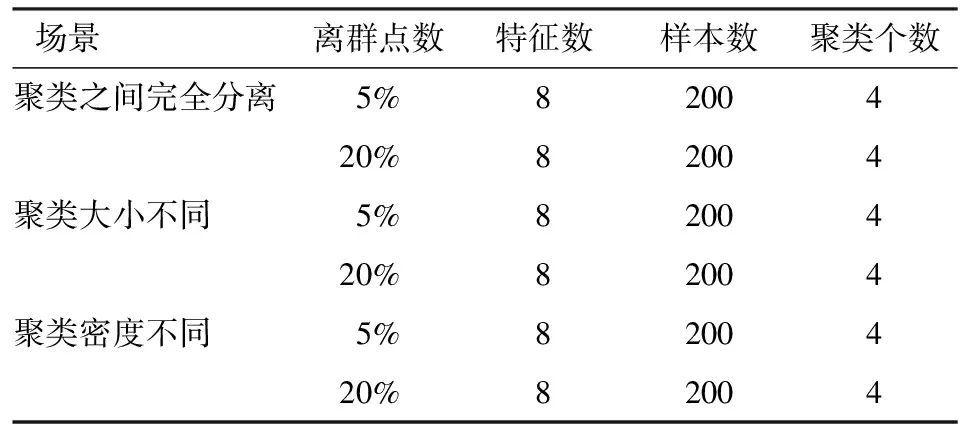
表1 仿真数据场景设置

1.ODA-SCG算法和已有的离群点经典算法K-means-算法、DBSCAN算法的精确性和稳定性比较

为了评价基于样本节点连通图的离群点检测算法(ODA-SCG)在离群点个数确定、离群点辨识准确度以及识别稳定性方面的性能，应用该算法分析每种实验场景产生的仿真数据(表1)，并与K-means-算法和DBSCAN算法对比。K-means-算法需要确定的参数包括聚类个数k以及离群点个数l，本文采用KL指标来辅助确定K-means-算法的最优聚类个数，在取最优聚类个数的情况下，设置K-means-算法中离群点个数l取值上限为样本数的20%，即40个，在该区间内分别取值为4、9、14、19、24。DBSCAN算法可以自动地识别聚类个数并将低密度区域的样本点视为离群点，但需要确定邻域半径eps和给定邻域内的最小包含点数MinPts这两个参数，设置扫描半径eps的取值区间为[0.1，10]，在该区间内分别取值为2、3、4、5、6，MinPts的取值为R中DBSCAN算法中的默认值MinPts=5。在基于重复聚类和节点连接图的离群点挖掘算法中，最大离群点个数的取值等于K-means-算法中离群点个数l的取值上限，设置连接强度δ取值分别为0.2、0.3、0.4、0.5和0.6，这样可以保证每个算法的参数变动幅度相同，从而使得结果具有可对比性。对比结果如图3～5和表2所示。其中，图3～5每一组第一个柱形图表示K-means-算法下的结果，第二个柱形图表示DBSCAN算法下的结果，第三个柱形图表示ODA-SCG+K-means-算法下的结果，第四个柱形图表示ODA-SCG+DBSCAN算法下的结果。

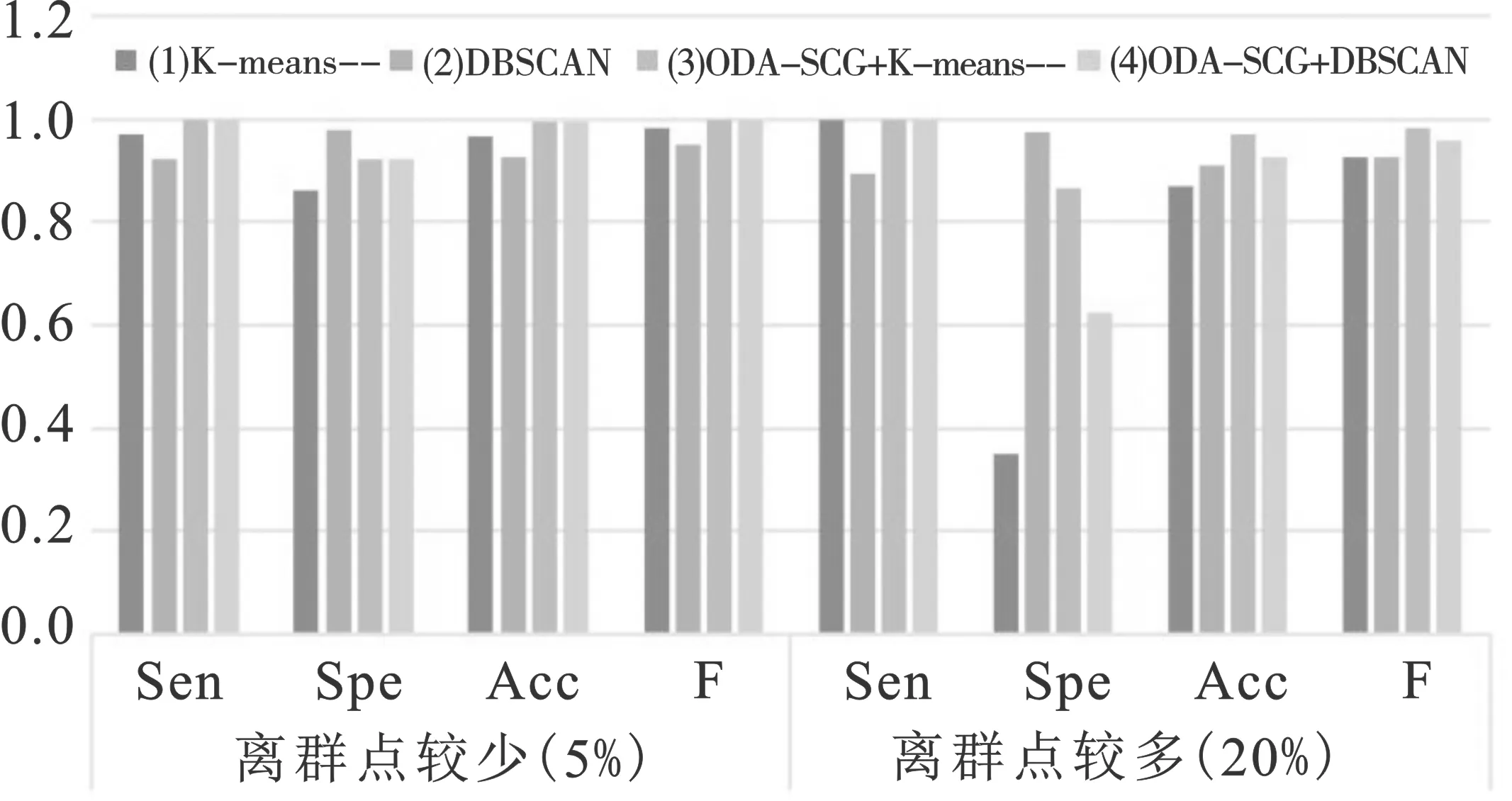
图3 聚类之间完全分离

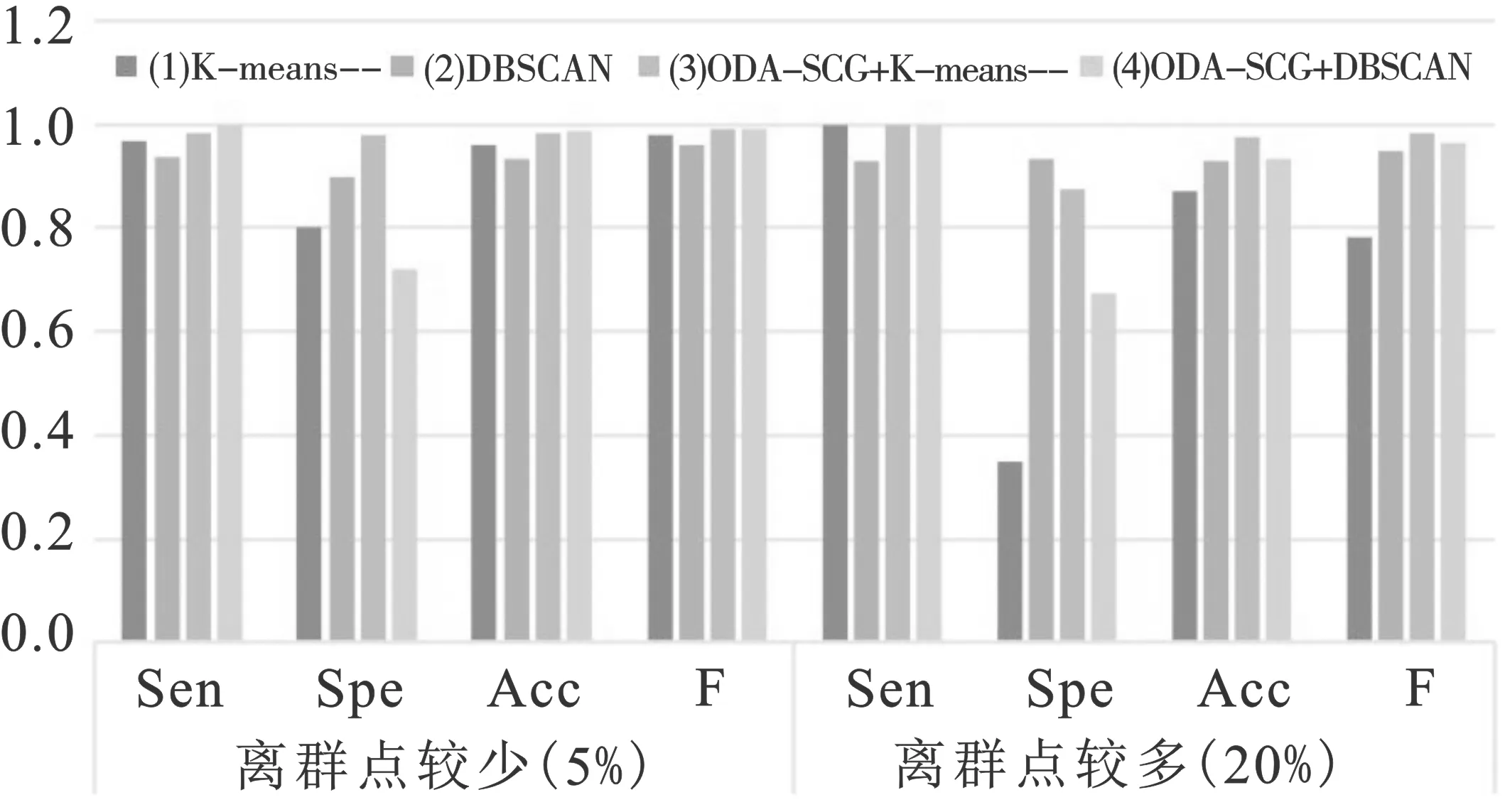
图4 聚类大小不同

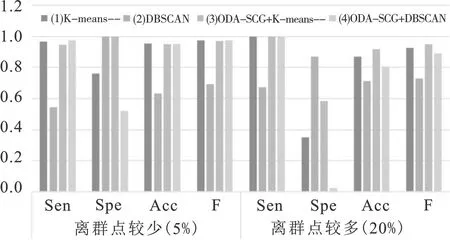
图5 聚类密度不相等

在算法准确度方面，ODA-SCG算法的灵敏度、特异度、准确度和F-measure值均较高，这说明ODA-SCG算法具有较高的准确度。只有当K-means-算法和DBSCAN算法的参数设置正确的时候，这两个算法才具有较高的准确度，而若参数偏离正确的取值，其离群点检测结果也将差于ODA-SCG算法。

用三种算法对表1中的三种仿真数据进行分析。可见，ODA-SCG算法相比其他两种算法而言离群点个数的变化幅度变化较小，更为稳定。

表2 几种算法的精确性和稳定性比较

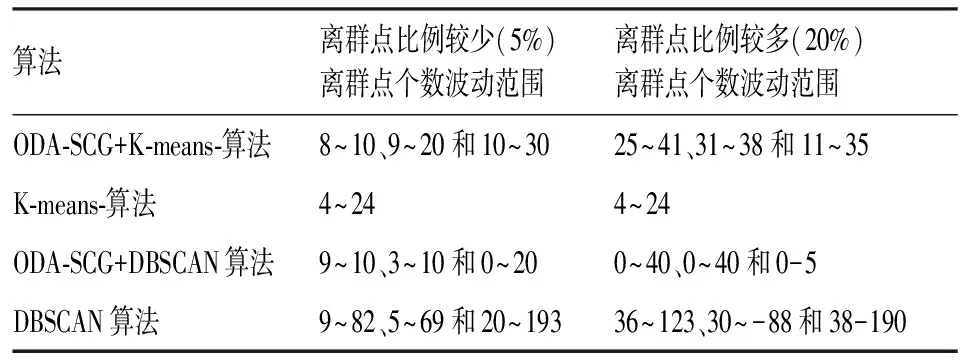
表3 离群点个数的变化幅度

综上所述，若不能够准确给定K-means-算法和DBSCAN算法的参数，ODA-SCG算法将具有更好的优势，它的离群点个数波动范围相对较小，且具有较高的准确度。

2.黄金标准数据方法和ODA-SCG算法的比较

我们的实验数据取自于“TREC-7Ad Hoc and TREC-8 Filtering Topics”中的四个主题。这四个主题分别是：

编号:351 福克兰石油勘探；

编号:357 领海争端；

编号:358 血液酒精中毒；

编号:360 毒品合法化好处；

我们找到TREC会议的相关性文档，从提供的中央情报局对外广播情报处数据中选取了 690条作为我们的候选集合，其中含有560条不相关文档，130条相关文档.我们选取了50名工作者作为测试者。

为了更直观地比较在标准数据答案下的准确率和在离群点算法估计答案下的准确率程度，我们把在两种情况下的准确率用折线图呈现，如图6所示，两种方法的走势非常相似，而且新的方法的结果更精确。这说明利用离群点算法估计的答案来对工作者进行评估是可行和有效的，这也使得本文提出的离群点算法策略在实际中具有良好的可行性。

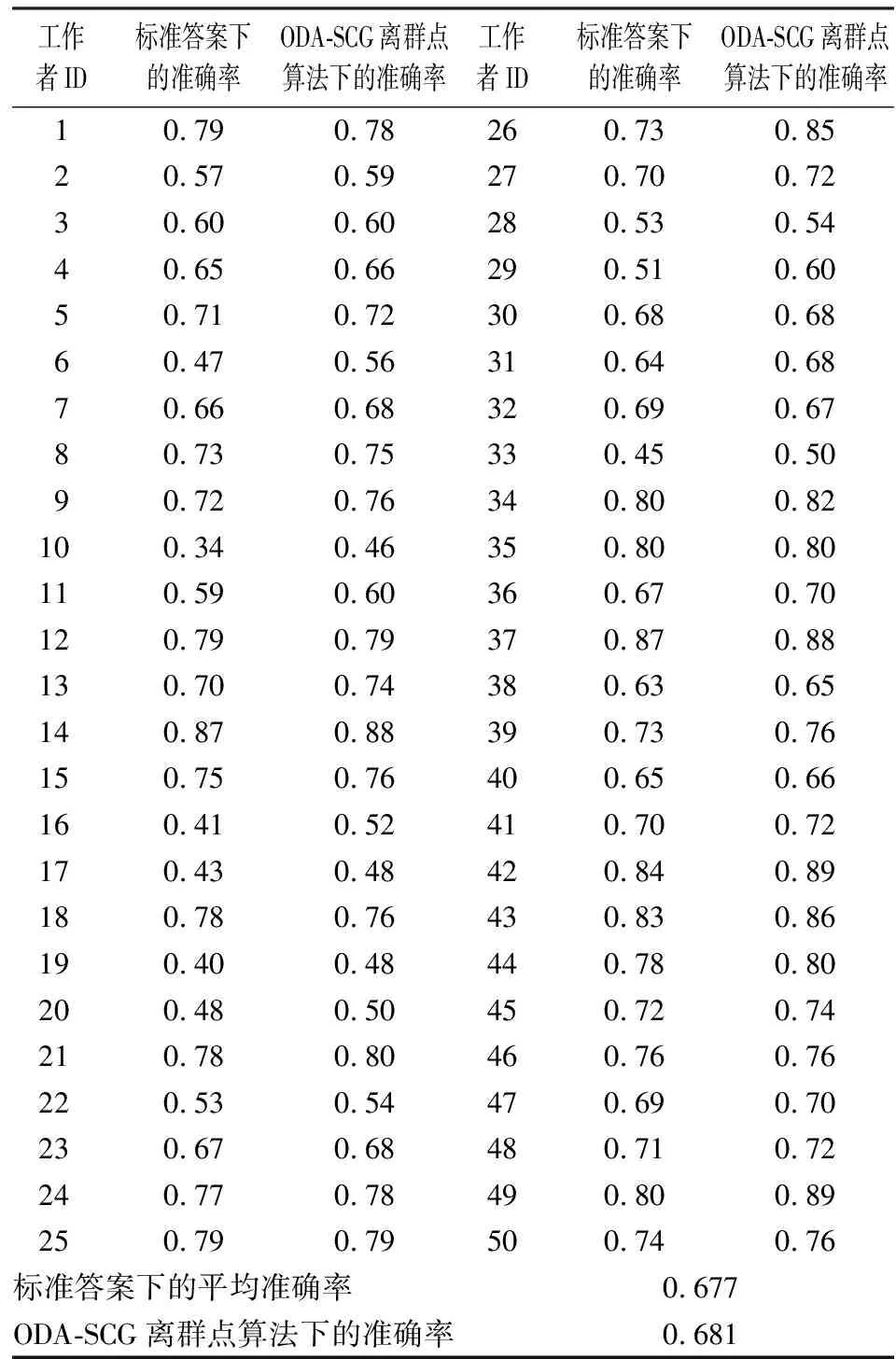
表4 工作者在标准答案和ODA-SCG离群点算法下的准确率比较

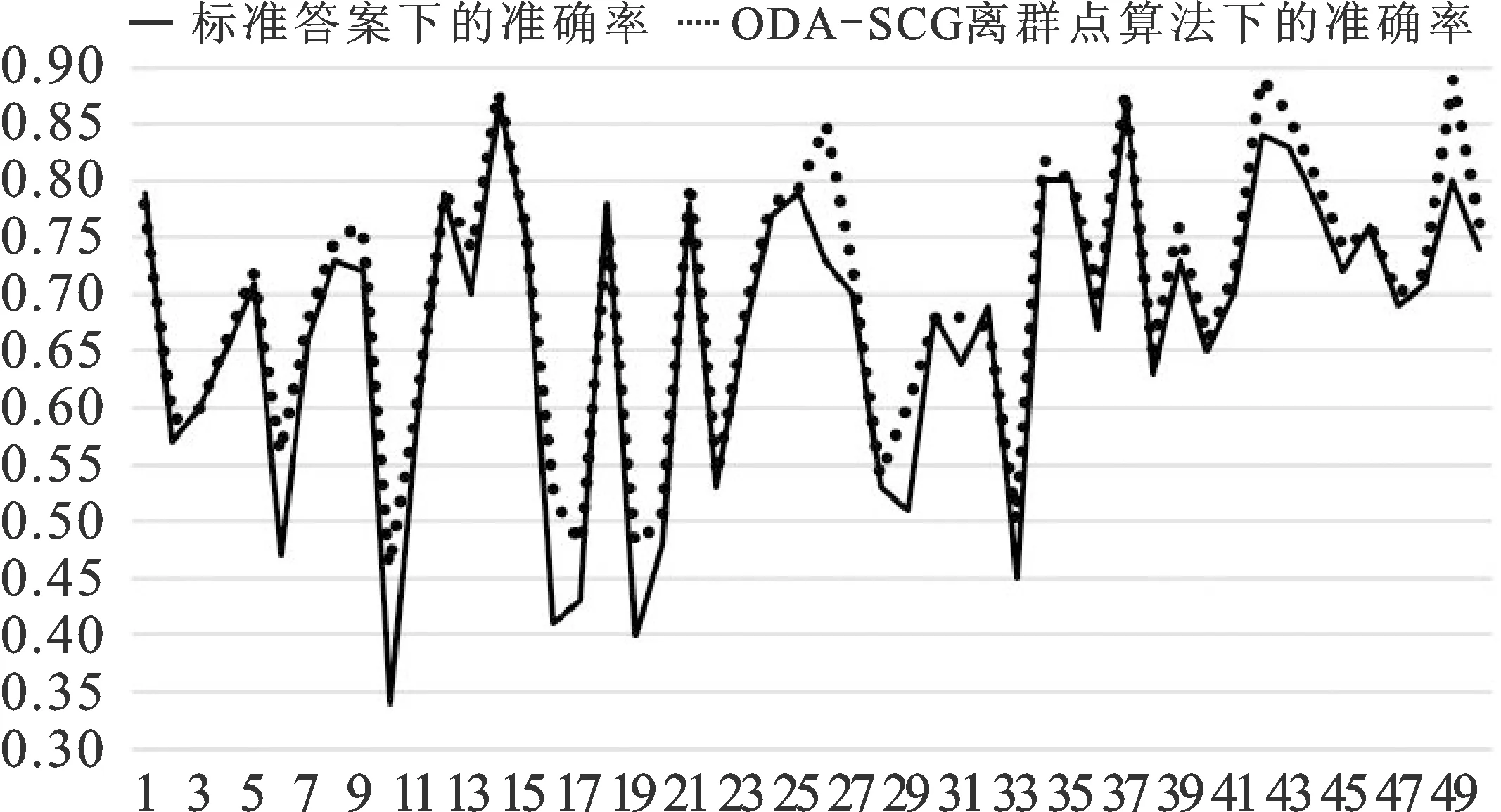
图6 两种策略比较

四、总结

本文通过给定参数范围、重复调用离群点检测算法来计算样本之间的连接强度，并给定连接强度下界的情况下构造样本连通图，再根据样本之间的连接关系确定离群点，提出了基于样本节点连通图的离群点检测算法(ODA-SCG)。该算法的创新之处在于，一是放宽了基于聚类的离群点识别算法(如：K-means-算法和DBSCAN算法)的参数设置，把给定具体参数数值改为给定参数范围；二是通过样本的连接图来判别离群点，这种方式更加直观。仿真实验结果表明，该算法能够放宽参数设置的范围，减少离群点个数波动范围，提升离群点识别准确率。当连接强度下界δ取值发生变化时，离群点的个数变化范围幅度不大，且离群点识别准确度较高，优于K-means-算法和DBSCAN算法。三是我们提出了一种新的众包的欺诈检测方法就是利用离群点检测算法。把经典的黄金标准答案和新的离群点检测算法做比较，发现离群点检测算法在准确性上优于黄金标准答案。

众包竞赛由于能够充分发掘社会大众的智慧而被企业广泛的应用，然而来自解答者和发起者两方面的欺诈行为导致众包竞赛效率下降。该离群点检测算法可以用来检测不合理的众包解答答案，从而筛除欺诈者，以期为众包竞赛双方营造相互信任的交易环境为进一步激励用户提供有价值的参考。因此优化欺诈者筛除机制将有助于众包竞赛健康发展。因此，在未来的研究中，将拓展算法的应用，把其他离群点挖掘算法融入到本文的算法中，拓展该算法的适应性和使用范围。