中国服务业增长和波动的区制转换与非对称性研究

王艺枞，陈 磊，b，孟勇刚

(东北财经大学a.经济学院；b.经济计量分析与预测研究中心，辽宁 大连 116025)

一、引言

自2013年起，中国经济进入新常态，经济增速换挡，产业结构优化升级，第三产业日益壮大。根据国家统计局发布的数据，2017年服务业(第三产业)增加值占GDP比重已达到51.6%，成为拉动经济增长的产业主体。另外，根据联合国统计司的数据，美国等发达国家的服务业增加值占比已经超过80%。由此可见，在发达国家已经进入以服务业为主导的经济时代趋势下，中国也在由“工业型”经济向“服务型”经济转变。因此，对服务业的波动进行测定和阶段划分成为当前经济新常态背景下的重要课题。

在国外对服务业周期的研究中，Layton等最早基于美国服务业数据构建了服务业一致指数和先行指数，此后除了Arti 等基于月度数据对印度服务业周期波动进行测定，未见其他对服务业周期的系统研究[1-2]。受限于中国统计部门公布服务业相关数据的频率和种类，中国服务业的景气周期研究也并不多见，王小平等基于年度数据构建了中国服务业一致指数、先行指数和滞后指数，但年度景气指数的政策参考性和时效性较差[3]；陈磊等用混频方法构建了服务业月度一致指数，并对中国服务业周期波动特征进行考察[4]。

在众多服务业一致指标中，服务业增加值作为对服务业景气代表性最强且包含信息最完整的指标，却因其发布频率为季度而无法与其他月度指标共同使用。而混频动态因子模型的出现解决了这种利用不同频率指标构建景气指数的难题。Mariano 等认为将季度GDP引入动态因子模型有两点好处：首先，通过加入GDP包含的信息可提高模型的功效；其次，可将共同因子理解为潜在月度实际GDP的增长率，因此他们基于季度GDP环比增长率和潜在月度GDP环比增长率的逻辑算式构建月度一致指数对美国经济周期进行监测[5]。Aruoba 等在动态因子模型中引入加总算子并提出了基于GDP同比增长率的混频动态因子方法[6]。随后，Camacho 等将马尔科夫结构引入混频动态因子模型，从而可对混频经济变量的协同性和非线性进行分析[7]。值得一提的是，以上研究往往只在截距项加入马尔科夫结构来判断经济增速的区制转换，而Kholodilin在截距项和方差项中均引入了马尔科夫结构，即四区制马尔科夫结构，同时考察美国经济周期的增速和波动的区制转换[8]。

国内基于混频模型对经济周期的研究较多[9-12]，但未见在服务业周期和波动研究中的应用，且多数对经济周期的阶段划分或非对称性研究也仅基于增长速度层面将景气周期划分为扩张和收缩两个阶段。因此，本文采用四区制马尔科夫结构下的混频动态因子模型，兼顾服务业增加值在服务业景气周期分析中的重要性和对服务业周期特征追踪的时效性，来刻画服务业周期的非线性、协同性特征。此外，本文通过计算服务业一致指数在各区制下的滤波概率来刻画服务业波动在不同时期的阶段性特征，从而将服务业一致指数划分为高增长―高波动、高增长―低波动、低增长―高波动和低增长―低波动四个阶段。最后，结合联合转移概率矩阵，分析在当前阶段中国服务业可能出现的转移路径和波动形态。

二、模型构建

(一) 四区制马尔科夫混频动态因子模型

依据服务业季度增加值与其潜在月度增加值的关系，设定Yt，1(t=1，2，3，…，T)为每季度可以观测到一次的服务业增加值序列，那么Yt，1满足：

(1)

(2)

但是，基于这一数学关系计算不可观测月度增长率会使相应的状态空间形式出现非线性结构，令模型变得复杂而难以估计。因此，本文基于Mariano等使用的处理办法[5]，将式(2)中的算术平均数算式改写为几何平均数算式：

(3)

从而得到：

(4)

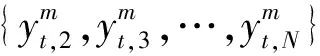
(5)

这里ft的系数矩阵{β1，β2，…，βN-1}′为因子载荷矩阵，{ut，1，ut，2，…，ut，N-1}′为异质性成分，本文将其设为协方差平稳过程，ft表示为如下的动态过程：

(6)

(7)

(8)

式(8)中，st表示基于相互独立的截距项和随机误差项划分的高增长―低波动、低增长―低波动、高增长―高波动以及低增长―高波动四个区制。pij表示上述四个区制间的转移概率矩阵，本文将其分别设定为：

(9)

式(10)表示异质性成分ut的动态过程：

(10)

其中，φu(·)表示q=max{q1，q2，…，qN-1}阶自回归系数，L表示滞后算子。

(11)

这里式(6)与(10)、(11)共同构成了包含四区制马尔科夫结构的混频动态因子模型。为了识别模型，本文对模型季度指标的因子载荷β1施加识别性约束条件，令β1等于1，同时将共同因子和异质性成分均设定为一阶自回归过程。

(二)模型的估计

为了对模型进行估计，将四区制马尔科夫结构下的混频动态因子模型写成式(12)和(13)组成的状态空间结构：

yt=Hβt+ξt

(12)

βt=λSm+Fβt-1+ζt

(13)

式(12)为量测方程，随机扰动向量ξt～N(0，R)；式(13)为状态方程，随机扰动向量ζt～N(0，Q)。共同因子ft和异质性成分μt均为不可观测，H、F分别为测量矩阵和转移矩阵；βt=(ftμt)′，ft=(ftft-1…ft-r)′，r=max(p，3)；μt=(ut，1ut-1，1…ut-l，1ut，2…ut-qN-1，N-1)′，l=max(q1，3)；λSm=(μst0 … 0)′。

这里yt为包含大量缺失值的经济序列，主要原因在于中国发布的部分月度指标在一些特定月份存在缺失值，且季度指标在不发布数据的月份无法观测。因此，本文参考Mariano等对缺失值的处理办法[5]，将式(12)改写成如下形式：

改写后的量测方程为：

(14)

然后，可以采用Hamilton滤波、Kalman滤波和Kim近似的极大似然估计法对式(13)和式(14)组成的四区制马尔科夫动态因子模型进行估计，得到不可观测变量βt和状态变量st的平滑估计值和滤波估计值。

三、指标选取与处理

本文收集了涵盖第三产业和细分服务行业的总量、投资、价格、调查指数和预期等多个方面的指标，数据来源于国家统计局网站和万得数据库，将基准指标定为服务业增加值同比增长率，采用K-L信息量和时差相关分析等方法对所选指标进行进一步筛选，并将所有水平值转化为同比增长率。关于同比增长率的计算，本文参考陈磊等的处理办法，优先采用统计部门或者机构发布的以可比价格计算的实际同比增长率，对于缺乏官方数据的指标，由该指标累计值或者水平值推算其实际同比增长率，最后得到的服务业一致指标如表1所示[14]。

表1 服务业一致指标

表1中的服务业增加值同比增速为基准指标，非制造业PMI和财新中国服务业PMI共同代表了服务业的商务活动情况，其中，非制造业PMI的调查对象主要为大型企业，财新中国服务业PMI的调查对象主要为中小私营企业，且这两项调查指数与服务业增加值的相关程度是最高的。消费者信心指数从经济意义上反映了消费者对经济形势的预期和主观感受，且消费需求与服务业紧密相关，由此将其作为服务业一致指标。规模以上港口货物吞吐量代表了交通运输业港口货物运输的运行形势，社会消费品零售额作为批发零售业运行情况的重要代表指标，且上述两个行业均为第三产业的重点行业，因此一并入选服务业一致指标。

考虑到中国数据发布特点，部分指标存在数据缺失情况，如规模以上港口货物吞吐量在12月的数据缺失，且一致指标在1月份和2月份的数据受春节因素的影响波动较大，本文将这些异常点视为缺失值，根据前文介绍的方法在状态空间模型的框架下予以解决。

由于式(4)中季度服务业增加值同比增长率与不可观测的月度实际服务业增加值同比增长率序列之间的近似关系是基于原始数据推导得出，若对指标进行季节调整，二者之间的关系不一定满足式(4)的关系。另外，本文所选指标多数为同比增长率或者经过同比调整的调查指数，不存在明显的季节效应。因此，本文将对未经季节调整的原始序列进行建模。

四、实证分析

(一)实证结果

为使模型估计简便，本文对所有服务业一致指标进行了标准化处理。另外，将服务业增加值季度同比增长率的因子载荷约束为1，使得提取的共同因子有直观的经济意义。表2中β对应式(5)中各一致指标的因子载荷，可作为判断各一致指标对共同因子提取贡献程度的依据；φf和φu分别为共同因子和异质性成分的自回归系数；σf和σu分别表示共同因子和异质性成分的标准差，代表二者的波动程度，且根据σf的数值可对共同因子的波动区制进行划分；μ表示共同因子在各区制下的截距项，可根据其数值划分增长区制；pii对应式(7)中的转移概率；括号内为参数对应的标准差；L为模型的对数似然值。

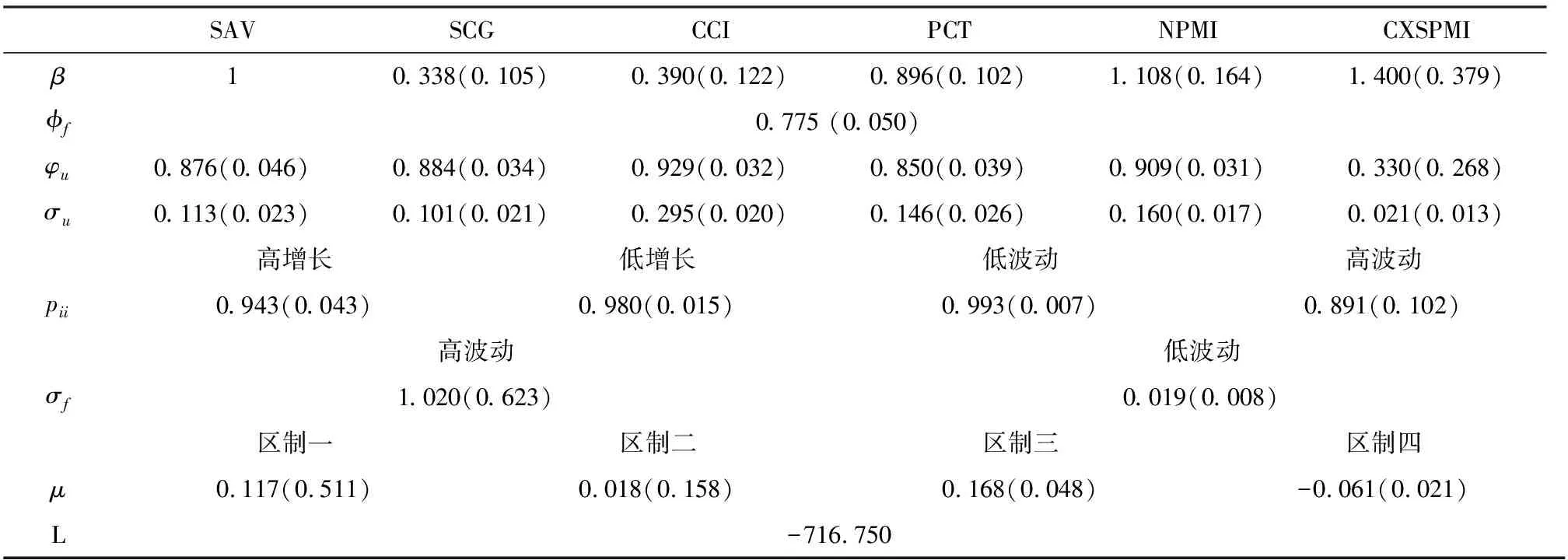
表2 模型参数估计结果

从参数结果可知，第一，模型中的所有参数均在5%显著性水平下显著，本文提取的共同因子，即服务业一致指数在服务业增加值实际同比增长率、规模以上港口货物吞吐量同比增长率、非制造业PMI和财新中国服务业PMI等变量上的载荷明显占优，分别为1、0.896、1.108和1.400，这与指标筛选过程中各指标与基准指标的相关性结果基本一致，而社会消费品零售总额同比增长率和消费者信心指数对共同因子提取的影响有限。估计结果显示，消费者信心指数与其他一致指标相比，异质性波动成分明显更高，说明消费者信心指数较高的波动程度影响了它对服务业一致指数的贡献；而社会消费品零售总额同比增长率与服务业增加值同比增长率和其他四个服务业一致指标的时差关系相对滞后，同期相关性较小，因此该指标对提取服务业一致指数的贡献较低。

第二，服务业一致指数的自回归系数约为0.775，当服务业受到外生冲击后，冲击成分的半衰期约为2.7个月，服务业需要约9个月来消除90%以上的影响，在一定程度上说明中国服务业的自我调节和稳定机制相对较强，没有很长的波动持续期。这一结果符合服务业的内在运行特征。由于服务业生产消费的同时性和服务产品的特殊性，成熟市场经济体下的第三产业波动显著低于宏观经济以及第二产业的波动[15-16]。

第三，服务业一致指数两个波动区制下的标准差存在明显的差异，其值分别为0.019和1.020，并且高波动状态下的标准差远高于低波动下的标准差，这说明服务业一致指数可以被划分为低波动和高波动两种区制，且本文对服务业两种波动区制的区分力度较大。

第四，pii的估计值分别为0.943、0.980、0.993和0.891，由于持续期Di=1/(1-pii)，因此可由转移概率推断出中国服务业景气处于高增长阶段的持续期为17.54个月，处于低增长阶段的持续期为50个月，约等于高增长阶段的三倍；高波动阶段的持续期为9.17个月，低波动状态的持续期为142.86个月，约等于高波动阶段的14倍，说明在样本期内中国服务业以低速增长为主，且主要在以低波动为主的“大稳健”时代。

第五，服务业一致指数在高波动区制下的截距项分别为0.117和0.018，并且在5%的显著性水平下显著异于零，代表了中国服务业的高增长―高波动(区制一)和低增长―高波动(区制二)阶段。在低波动区制下的两个区制分别表示中国服务业的高增长―低波动(区制三)和低增长―低波动(区制四)阶段。此外，高增长―高波动区制与低增长―高波动区制间的截距项之差显著大于高增长―低波动、低增长―低波动区制之间的截距项之差，即增长率“缺口”；同样地，高增长―高波动与低增长―高波动之间μ的标准差之差也显著高于高增长―低波动与低增长―低波动下μ的标准差之差，说明服务业一致指数由高波动转向低波动的过程同时伴随着服务业增速的平稳化过程。

(二)中国服务业周期的阶段性变化

通过状态变量st的滤波估计值结果，服务业处于低增长阶段即景气收缩阶段的滤波概率由图1给出，图2描述了服务业一致指数处于高方差即高波动状态下的滤波概率，低增长阶段滤波概率为高波动―低增长和低波动―低增长滤波概率相加，高波动阶段滤波概率为高增长―高波动和低增长—高波动阶段下滤波概率相加。本文参考Chauvet等提出的以概率值为0.65和0.35为分界点的判定准则，对服务业增长与波动阶段进行划分[17]：若向前一期服务业在高增长阶段且当期服务业在低增长阶段的概率大于0.65，可判定当期服务业已进入低增长阶段；若向前一期服务业在低增长阶段且当期服务业在低增长阶段的概率小于0.35，可判定当期服务业进入高增长阶段；阶段转移后持续期应大于两个月，波动阶段的划分同理。阴影部分表示由以上准则确定的服务业周期阶段。

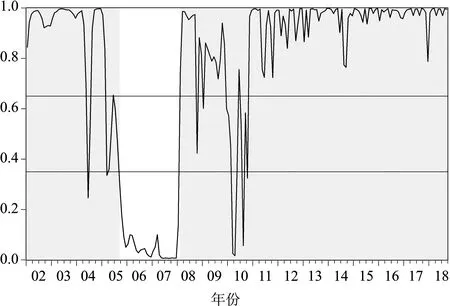
图1 服务业景气处于低增长阶段的滤波概率

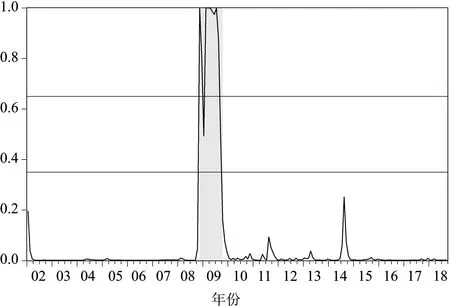
图2 服务业景气处于高波动阶段的滤波概率

图1显示，中国服务业的低速增长阶段主要有：2002年1月至2005年9月，2008年2月至2018年9月；图2显示，中国服务业的高波动阶段主要有：2008年11月至2009年10月。2002年以来，服务业增速的波动比较缓和，仅在2005年9月和2008年2月出现过不同增长速度状态的转换；波动方面，服务业以低波动状态为主，仅在2008年11月出现了一个高波动状态，持续时间为12个月。

图3和图4分别给出了服务业一致指数在四个区制下的滤波概率。样本期内，中国服务业景气波动以低增长―低波动为主，其次为高增长―低波动状态。

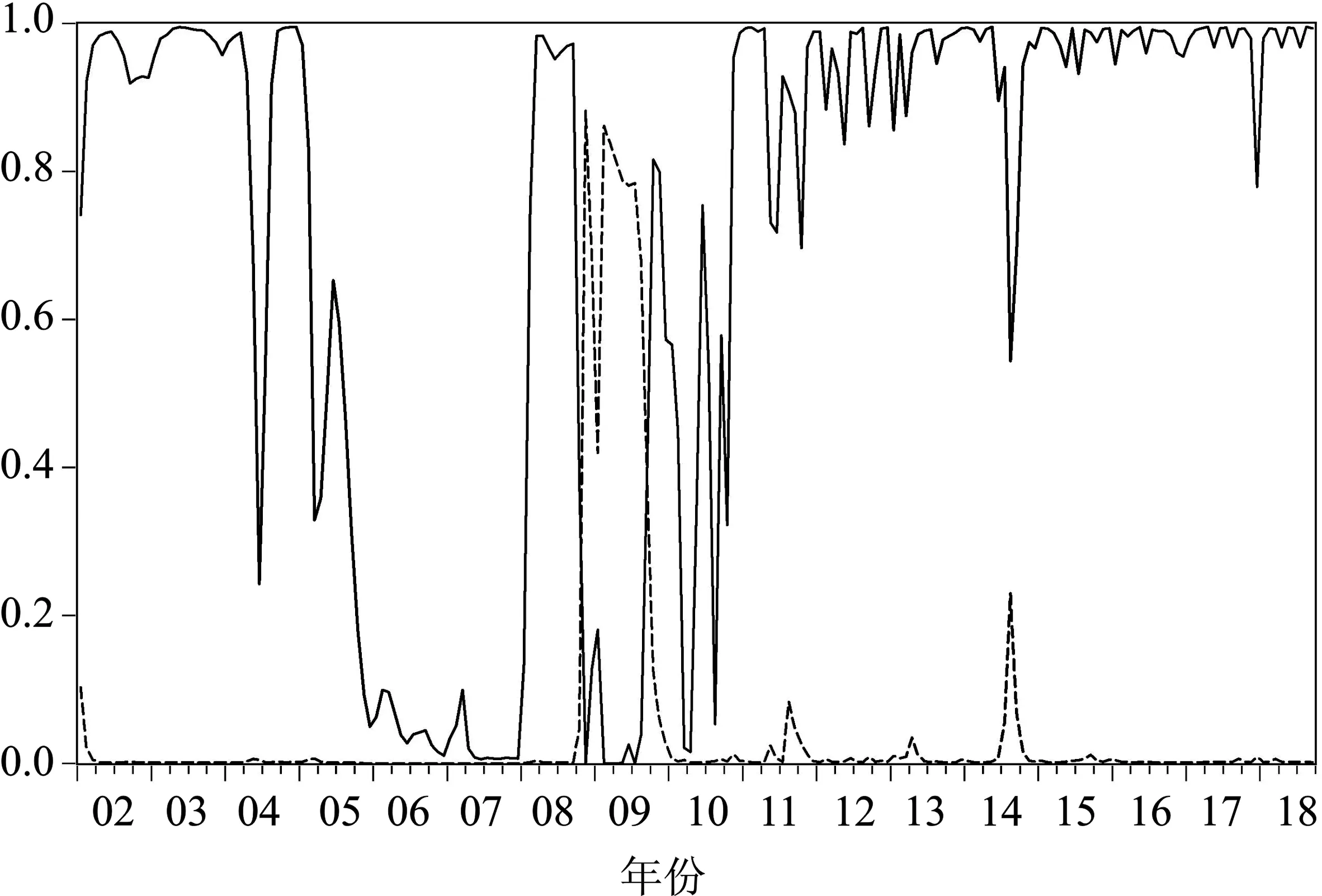
图3 低增长―低波动(实线)和低增长―高波动(虚线)状态的滤波概率

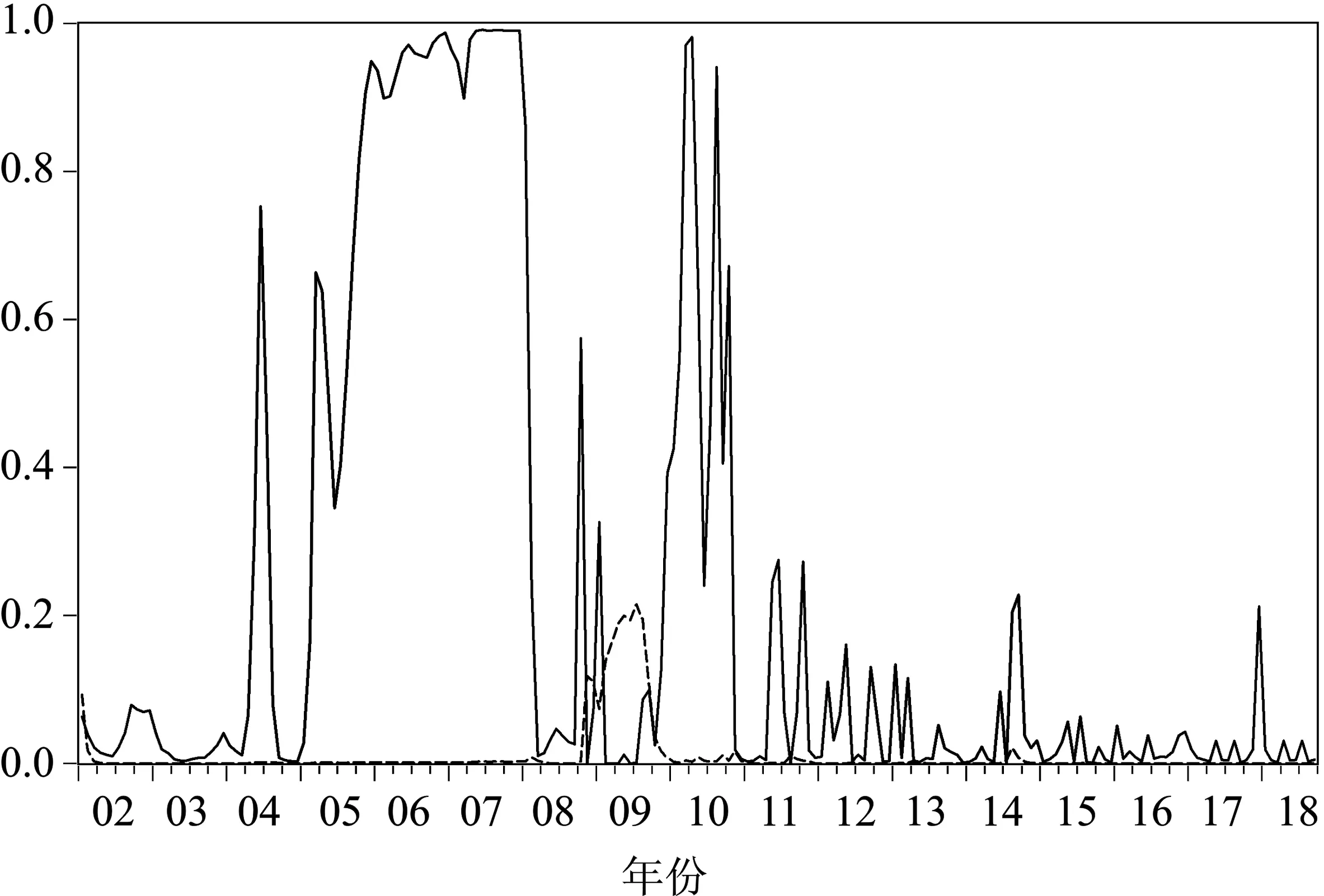
图4 高增长―低波动(实线)和高增长―高波动(虚线)状态的滤波概率

根据共同因子的滤波概率可得到中国服务业增长和波动的区制划分结果：2002年1月至2005年9月为低增长―低波动阶段，2005年10月至2008年1月为高增长―低波动阶段，2008年2月至2008年10月为低增长―低波动阶段，2008年11月至2009年10月为低增长―高波动阶段，2009年11月至2018年9月为低增长―低波动阶段。服务业的增长与波动在样本期内具有明显的阶段性特征，具体来看，2002年1月至2005年9月中国正处于经济体制和市场环境转换的经济低速调整期，受宏观经济大环境影响，中国服务业在此期间处于低增长―低波动阶段，并在2004年6月出现了一次服务业增长速度的“陡升陡降”。随着经济环境的改善及各服务行业如房地产市场的繁荣，2005年10月至2008年1月，中国服务业经历了持续期为28个月的高增长―低波动阶段。2008年2月至2008年10月，受当时中国宏观调控政策收紧影响，中国服务业再次进入低增长―低波动阶段，而这一次的低增长―低波动阶段仅持续了9个月。此后，受金融危机和随后当局出台的一揽子刺激经济计划及后续引发的产能过剩和房地产泡沫等问题的影响，服务业景气波动较为剧烈，在2008年11月至2009年10月期间，中国服务业处于低增长―高波动阶段，这也是样本期唯一的一次服务业高波动时期，且仅持续12个月。服务业较强的自我调节能力和稳定机制使得2009年11月至2018年9月，即从2009年11月开始直至样本期结束，中国服务业一直处于低增长―低波动阶段。在这一阶段，尽管中国服务业增长速度在2010年出现过短暂的反弹，但持续期较短，未能使服务业景气由低增长状态向高增长状态转移。

表3列出了不同增长状态和波动状态的联合转移概率矩阵。由表3可以看出：第一，增长区制相同时，不同波动区制之间的转移概率具有明显非对称性。其中，高增长―低波动区制转移至高增长―高波动区制的概率(0.006 6)显著低于由高增长―高波动区制转移至高增长―低波动区制的概率(0.102 8)。这意味着在服务业高增长时，更容易出现高增长―高波动状态向高增长―低波动的转移的情况。同样的现象也发生在低增长区制下的高低波动区制之间的转移，即由低增长―高波动阶段转向低增长―低波动阶段的可能性更大。

第二，波动区制相同时，不同增长区制之间的转移概率也存在非对称性。在高波动区制下，由高增长―高波动转移至低增长―高波动的概率(0.050 8)显著高于由低增长―高波动转移至高增长―高波动的概率(0.017 8)。在低波动区制下，由高增长―低波动向低增长―低波动转移的概率(0.056 6)显著高于后者向前者转移的概率(0.018 6)，说明服务业无论是在高波动还是低波动状态，从高增长区制转移至低增长区制的概率都要大于后者转移至前者的概率。

第三，由前两点结论并结合表3不难发现，无论服务业在何种区制下，除了保持原有状态不变，都倾向于转向低增速或低波动状态，如服务业在高增长―低波动、高增长―高波动、低增长—高波动区制下，若发生区制转移，分别最有可能转入低增长―低波动、高增长―低波动和低增长―低波动区制，这与服务业的平缓波动特征相符。

第四，在当前经济新常态时期，中国服务业正处于低增长―低波动的平稳阶段，在低增长―低波动的新常态背景下，维持原有状态的概率(0.973 1)远远高于服务业向高增长―低波动、高增长―高波动和低增长―高波动三个区制转移的概率(分别仅为0.018 6、0.000 1和0.006 9)，这说明中国服务业保持在低增长―低波动阶段的可能性非常高。若服务业的区制状态发生变化，转入高增长―低波动阶段的可能性最大，之后最有可能以0.936 4的概率维持在原有状态，或者以0.056 6的概率进入低增长―低波动阶段，形成低波动―高增长与低波动―低增长阶段交替出现的波动态势。综上所述，中国服务业波动会以当前低增长―低波动状态作为“L”型运行特征的底部平稳运行，短期内不太可能出现“U”型反弹态势，有可能会出现高增长―低波动与低增长―低波动两种区制状态交替的“W”型波动态势。

表3 联合转移概率矩阵

五、结 论

本文选取服务业增加值实际同比增长率、非制造业PMI、财新中国服务业PMI、消费者信心指数、规模以上港口货物吞吐量同比增长率和社会消费品零售额同比增长率构成混频一致指标组，采用四区制马尔科夫混频动态因子模型从服务业增长高低和波动强弱的双重角度对中国服务业周期的运行特征进行分析，主要结论如下：

第一，服务业一致指数的提取受服务业增加值实际同比增长率、规模以上港口货物吞吐量同比增长率、非制造业PMI和财新中国服务业PMI这四个指标的影响较大。中国服务业一致指数波动的持续性不会太强，当服务业受到外生冲击时需要约9个月来消除90%以上的影响，说明中国服务业的自我调节和稳定机制相对较强。

第二，服务业一致指数在四个区制状态下的滤波概率显示，中国服务业景气波动以低增长―低波动为主，其次为高增长―低波动状态。2002年1月至2008年10月，中国服务业在低波动―低增长与低波动―高增长两个状态之间的交替往复。2008年11月至2018年9月，中国服务业周期呈现出在低增长―低波动与低增长―高波动之间交替往复，但低增长―低波动状态占主导地位。

第三，增长区制相同时，高波动与低波动区制之间的转移概率具有明显非对称性，更容易出现由高波动状态转入低波动状态的情况；波动区制相同时，高增速状态与低增速状态之间转移概率也存在非对称性，高增长状态向低增长状态转移的可能性更高。当前，服务业景气会在以低增长―低波动为主要特征的“L”型底部运行，短期内出现“U”型反弹的可能性不大，可能会在低波动水平上呈现高―低增长状态交替的“W”型波动态势。