机会不平等的测度：回归树模型的应用与比较

李金叶，郝雄磊

(新疆大学 经济与管理学院，新疆 乌鲁木齐 830046)

一、引言

改革开放以来，相伴于经济快速增长，收入分配差距不断扩大，国家统计局公布的基尼系数虽然处在“警戒线”0.4以上，但阶层对立和社会动乱的情况并未出现，一种解释是收入不平等中含有合理成分。决定个人产出的因素可以划分为努力因素和环境因素，前者是个体可控的，如教育程度、工作时间等，而后者是个体不可控的，如家庭背景、个体特征等。具有完全相同外生环境的个体属于同一环境类型，产出差异仅由个人努力决定，由于努力的差异性导致的类型内的产出不平等在道德上是无关紧要的，但类型间的产出差异是机会不平等所导致，是不合理的不平等，机会不平等程度越高，对经济主体生产性行为的负向激励就越严重，个体再分配倾向就越明显，家庭背景较差群体的社会不公平感也会更强烈。社会公众深恶痛绝的并非收入不平等，而是隐藏其中的由于外部不利环境因素造成的机会不平等，《深化党和国家机构改革方案》正是将促进社会公平正义、增进人民福祉作为改革的出发点和着力点。

本文首次将回归树模型应用到机会不平等测度中，而且构建了Ratio统计量来比较该模型与传统方法之间的优劣，是机器学习与经济学研究相结合的有益尝试。基于树的模型还包括分类树，因此该模型不仅适用于连续型产出变量，如收入，而且还可应用于分类型产出变量，如健康或教育，不仅补充了机会不平等测度的相关文献，也为传统的经济学研究提供新思路，具有重要的理论意义。在实践上，利用回归树模型可以测算出不同环境变量的相对重要性，为政府解决收入分配差距过大问题、实现以机会均等为核心的包容性增长提供切入点，本研究具有重要现实意义。

二、文献综述

基于Roemer的环境和努力二元分析框架，一系列机会不平等测度方法被提出，Fleurbaey等人将其划分为“事前”法和“事后”法两类[1]：前者依据环境类型不同对个体分组，用组间收入不平等来表示机会不平等[2-5]；后者依据努力类型不同对个体分组，用组内收入不平等来表示机会不平等[6-8]。由于努力程度难以像环境变量直接观测，通常采用人力资本、工作状态等间接反映[2，9]，但其可靠性常常受到质疑，“事后”法的应用存在极大局限性，本文是基于“事前”法测度机会不平等。

关于中国城镇居民机会不平等的实证研究，随着微观数据库建立而逐渐增多。江求川等利用CGSS、CHIPS和“社会结构与社会现代化”调查数据，通过非参数法测度1996-2008年城市居民机会不平等变化，发现机会不平等对于收入不平等的贡献在研究期内由25%上升到33%，且机会不平等程度在不同年龄组、性别和地区间存在明显差异[12]；陈东和黄旭锋利用CHNS数据，通过参数法测度出1989—2009年机会不平等对于收入不平等平均贡献达到54.61%，且出生地、父亲职业类型和户籍对于子女收入有显著正向影响[13]；胡在铭利用CHIP数据，基于参数回归不平等分解法估计出机会不平等占收入不平等程度达到33.3%以上，且性别和地区是影响机会不平等程度的决定因素[14]。上述研究主要关注于测算，宋扬在测度机会不平等基础之上进一步验证了劳动力市场歧视、教育代际固化是性别、户籍和家庭背景影响个体收入的主要途径[15]。

已有的研究为了解中国城镇居民机会不平等的问题提供了理论与经验依据，但不同学者的研究结论差异较大，一方面是因为所采用的参数法或非参数法均存在明显缺陷，另一方面是因为不同调查期的样本年龄分布不同，使得跨年比较存在样本差异问题。本文在Roemer的环境和努力二元分析框架基础上，利用CGSS2010、2011、2012、2013、2015数据进行研究，为避免环境变量选择的随意性，尽可能构造完备的环境集，选取了10个环境变量，基本涵盖了现有文献中所使用的环境变量。与已有研究相比，本文创新之处在于：第一，首次将回归树模型应用于机会不平等的研究，该模型可以自动筛选出重要环境变量，减少人为干预问题，为现有的研究提供更加客观的测度方法，其中条件推断树算法将环境变量与个体收入之间复杂非线性关系通过机会结构图展现，增加结果可读性，条件推断森林提高了结果可靠性；第二，依据年龄段而非调查期对样本分组，将个体置于特定社会变迁阶段中来测度不同环境变量对于个体收入重要性差异，并分析为何存在这种差异，提供了新的研究视角；第三，已有研究常以拟合能力为模型选择标准，而过拟合问题又会导致机会不平等程度被高估，因此本文构造Ratio统计量来比较不同模型的样本外表现，并利用bootstrap抽样获得统计量95%置信区间，拓展了现有的模型比较方法，更能解决实际问题。

三、算法说明

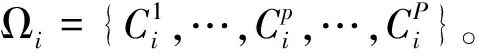
(一)条件推断树

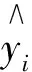
在机会不平等背景下，条件推断树得出一个特别的树形结构，每个假设检验本质上都是对特定子样本中是否存在平等机会的检验，如果算法并没有导致分裂，则不能拒绝机会均等的原假设。树形结构越深，越有必要考虑社会中存在的机会不平等，每次分割都意味着产生的环境类型间具有显著不同机会，在树的终端节点不能拒绝机会均等的原假设。

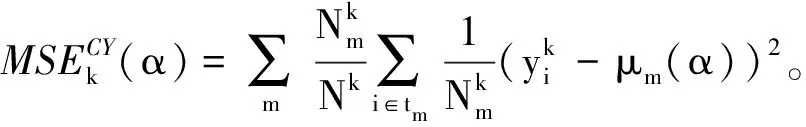
(二)条件推断森林

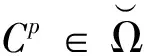
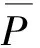
四、数据与描述性统计

本文采用的数据来自于“中国综合社会调查”(China General Social Survey)，调查区域涉及中国内地各省份，调查样本数超过10 000户，调查内容包括个体特征、就业、收入、家庭背景等方面。选取CGSS项目公布的第二期调查数据(9)CGSS项目第二期执行时间是2010—2019年。截止目前，最新公布是2015年调查数据，由于2014年做的是一项专题调查，数据仍处于清理阶段，暂不对外发布。为分析样本，具体包括2010、2011、2012、2013、2015年数据。

对于可测环境变量的选择，遵循国内学者相关研究，选取10个最常用的环境变量，如图1所示。产出变量选择个人全年总收入，并将其取对数。由于使用的是跨年数据，一方面，不同年份的样本，其年龄分布存在较大差异性，同一年内处于不同职业阶段的青年、中年和老年人，其收入也不具有可比性；另一方面，处于不同年龄段的人群见证了中国社会变迁的不同阶段，外部环境对于不同时间段出生的个体，在教育、就业和收入等方面影响机制存在差异。因此，本文将样本按照出生年代划分为不同年龄组：“50年代之前”“50年代”“60年代”“70年代”“80年代”“90后”。对于出生在50年代之前样本，年龄已达到70岁以上，其中大部分退出劳动力市场，本文删除此类样本。而“90后”样本主要以未成年人为主，仅有少数人刚刚进入劳动力市场，代表性不足，本文也剔除此类样本。

表1 环境变量说明

表2 按年龄分组统计

五、实证结果与分析

(一)机会结构

研究不同群体内部的机会结构，即分析哪些环境变量之间的差异导致机会不平等的产生，为政策执行提供充足的信息。条件推断树使得机会结构通过树的形式直观展示，相关重要信息直接呈现在图形中。采用数据驱动方法选择最优的显著性α水平，根据统计学相关准则设定α最优值在[0.001，0.1]区间内，以0.001为步长遍历区间内每个值。为避免单次交叉验证结果受到样本划分的影响，共进行10次10折交叉验证，并计算各α水平下对应的10折交叉验证均方误差的95%置信区间，如图1所示。最后综合考虑预测的偏差与方差(11)在各个年代组内，不同α得到不同均方误差和置信区间，根据其大小分别排名，将均方误差排名与置信区间排名相加，选择综合排名最小的α。，得出“50年代”“60年代”“70年代”“80年代”分别对应的最优α水平为0.055、0.077、0.097、0.075。

根据上述最优参数分别构建条件推断树模型得到机会结构，各个年代机会树终端节点数目分别为23、33、35、23，环境变量与个体收入之间均存在复杂非线性关系。考虑到文章篇幅限制，只列出“50年代”和“80年代”结构图(如图2和图3所示)，因为这两个年代年龄差异最大，机会结构图变化最为明显。对于50年代出生的个体而言，不同户口类型的个体机会均等的假设是最不被接受的，拥有非农户口的个体处于更有利的环境类型，样本量占比为45.46%，收入占比为66%，平均收入为31 865.206元，远高于农业户口个体13 673.841元。此环境特征优势取决于居住地差异，东部地区非农户口个体平均收入(37 539.682元)在统计意义上要显著高于西部、中部地区非农户口个体(25 353.232元)，西部、中部非农户口个体中若其父亲教育程度为小学以上水平，其平均收入可达到31 234元(终端节点26)，相反若其父亲教育程度为小学及以下，则性别成为影响个体收入主要因素。而性别这一因素对于居住在东部的非农户口个体而言产生的影响要高于父母教育程度。与之类似，影响农业户口人群收入的主要因素为居住地，而对于各地农业户口个体，性别是影响收入第一要素，其中性别为女、14岁时母亲就业状况为务农的农业户口个体，是50年代出生人群中收入最低的组，占到样本16.83%。相反，居住于东部、性别为男并且母亲接受过教育的非农户口个体是收入最高的组，占到样本的5.16%。

图1 显著性水平α的调整

图2 20世纪50年代出生个体的机会树

对于20世纪80年代出生的个体而言，居住地是影响人群收入最重要因素，平均来看，东部个体收入为47 701.261元，中部、西部个体收入为30 096.031元，收入的相对差距要低于其它年龄组。在东部地区，户口类型为非农户口且出生在外地的男性个体平均收入为60 730元，是80年代出生人群中收入最高的组，而出生在本地的个体其平均收入会受到母亲教育年数、性别的影响。在东部地区农业户口人群内部，性别是主要影响因素，而是否出生在本地主要影响男性个体，母亲就业状况主要影响女性个体。在西部、中部地区，出生在外地的男性其平均收入最高(终端节点36)，出生在本地的男性会受到14岁时父亲就业状况、父亲教育年数以及居住地影响。在西部、中部地区女性群体内部，个体14岁时父亲就业状况是主要影响因素，其中父亲为非正式就业或者无业或者务农，且母亲未接受教育的个体，其平均收入为16 830元，是80年代出生人群中收入最低的组。

图320世纪80年代出生个体的机会树

(二)环境变量重要性排序

采用条件推断森林需要确定树的数量、显著性水平以及每个分割点可使用的环境变量数目，为减少计算，事先将树的数量固定为200。设定α最优值在[0.001，0.1]区间内，以0.005为步长(12)在条件推断树模型中，对参数α进行调整时发现，当α在较小范围内变化时，均方误差并不会发生突变，因此将步长调整为0.005，以减少计算。遍历区间内每个值，环境变量数目P为4～8，构建不同的参数组合。为避免结果的随机性，通过设置不同随机数种子，在各参数组合下，计算5次out-of-bag均方误差并取其均值，以环境变量数目为分组变量进行拟合，如下图4所示。可以看到“50年代”“60年代”“70年代”“80年代”对应的最优的环境变量数目分别为6、6、5、5，对应的最优alpha值分别为0.085、0.090、0.080、0.085。

依据上述参数组合构建条件推断森林并计算变量重要性，为便于比较，对变量重要性进行标准化处理(13)以“50年代”为例，通过置换变量父亲教育年数、父亲就业状况、户口类型、家庭等级、居住地、母亲教育年数、母亲就业状况、是否出生在本地、性别，模型预测精度分别下降了4 038 639、1 126 782、69 473 057、1 477 543、38 349 859、3 823 320、4 667 311、3 721 947、24 399 685，标准化之后为0.058、0.016、1、0.021、0.552、0.055、0.067、0.054、0.351。，如图5所示。对于20世纪50年代出生的人群，户口类型重要性要远高于其他变量，1958年颁布《中华人民共和国户口登记条例》第一次明确区分“农业户口”与“非农户口”，随后又颁布相关政策条例进一步将劳动用工、教育、住房、社会福利等公民权益与户口衔接。计划时期所有劳动者被纳入统一的就业、福利和保障体系，意识形态上提倡妇女能顶半边天，由于性别产生的工资分配差异并不明显。

图4显著性水平alpha与环境变量数目P的选择

20世纪60年代出生的人口于80年代进入劳动力市场，正值市场机制引入就业体制，进入90年代后以提高生产效率和竞争力为目的的国企改革使得隐性失业显化，1998年统计国企下岗职工中女性为265.2万人，占到国企下岗总人数的44.6%，高于国企中女职工所占比重36.5%，并且下岗女职工再就业调查中，感觉受到性别歧视的占到49.7%，远高于男性18.9%(14)相关数据来自《2000年：中国社会形势分析与预测》。，伴随市场化程度的提高，劳动力市场呈现出性别分割现象。

对于20世纪70年代、80年代出生的人群，居住地重要性已超过性别与户口类型，他们的事业成型期处于社会主义市场经济体系初步建立之后，地区之间收入差距成为突出问题。由于在改革开放初期采取非均衡发展战略，东部沿海省份依靠地理位置优势得到重点发展，形成长三角、珠三角等增长极，而此时中西部地区在各个方面的发展全面落后。对于20世纪80年代出生的人群，变量重要性排序与70年代类似，但是否出生在本地的重要性超过了户口类型，排在第三位。一方面，20世纪80年代依次颁布了《国务院关于农民进入集镇落户问题的通知》《公安部关于城镇暂住人口管理的暂行规定》开始放松户籍严控制度，随后出台的系列政策措施都旨在促进有能力的外来人口在本地安家落户，户口类型所造成的实际利益不平等已逐渐弱化。另一方面，“80年代”的人事业起步于2000年，上一代的收入差距逐渐累计到他们身上，表现为家庭财富的差距，产生“富二代”现象，家境优越的父辈通常会选择搬迁到发展更好的地区为子女争取更多的资源，相对于普通家庭而言，此类家庭中的子女拥有更好发展轨迹。

横向来看，户口类型重要性不断下降，而居住地的重要性持续上升。观察14岁时父母教育年数、就业状况、家庭等级、是否出生在本地的重要性，在“50年代”基本一致，而“80年代”是否出生在本地、父母就业状况重要性在提升，家庭等级、父亲教育年数重要性在下降。

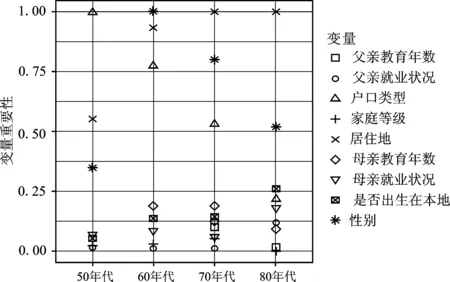
图5 变量重要性排序

(三)不同测度方法的比较

首先比较模型预测能力的差异，将样本随机分为训练集itrain∈{1，2，…，Ntrain}和测试集itest∈{1，2，…，Ntest}，其中Ntrain=2N/3，Ntest=N/3。利用训练集来拟合模型，利用测试集来比较不同模型的样本外表现(15)利用训练集拟合模型时，条件推断树、条件推断森林需要通过网格搜索法进行参数调优，后续为构造检验统计量又会重复此过程200次，为简化计算过程，将参数固定为整体样本的最优参数，即上文中求得的参数。。分别将参数法、非参数法、条件推断树在测试集上的均方误差除以条件推断森林的均方误差，构造统计量Ratio，若其值小于1，则说明该方法预测能力优于条件推断森林，重复上述过程200次，再通过bootstrap抽样得到检验统计量95%置信区间。观察Ratio箱线图，如图6所示，对于各个年代样本而言，非参数方法在测试样本上的均方误差要大于参数方法，而参数方法要大于条件推断树，条件推断森林预测能力要优于以上方法。从表3还可以看到，条件推断森林与条件推断树的估计结果最接近，Ratio的95%置信区间最窄，对应的箱线图分布也更为集中。进一步比较全样本下不同模型对于机会不平等测量结果的差异，如表4所示，对于各个年代样本而言，条件推断森林的估计值要远低于参数法和非参数法，而预测精度要高于后者，主要由于参数法与非参数法的分类存在过度拟合数据的现象。条件推断树的结果与条件推断森林最接近，但由于没能充分利用可测环境集中的信息，导致其预测精度低于条件推断森林。从表4纵向来看，无论采取何种方法机会不平等绝对程度都呈现出下降的趋势，而机会不平等的相对程度并未表现出一致性，依据条件推断森林的结果得出中国机会不平等的绝对和相对程度都在下降，“50年代”人群收入不平等中有35.3%是由外部环境因素引致的机会不平等，而在“80年代”人群中这一比例下降到19.8%。

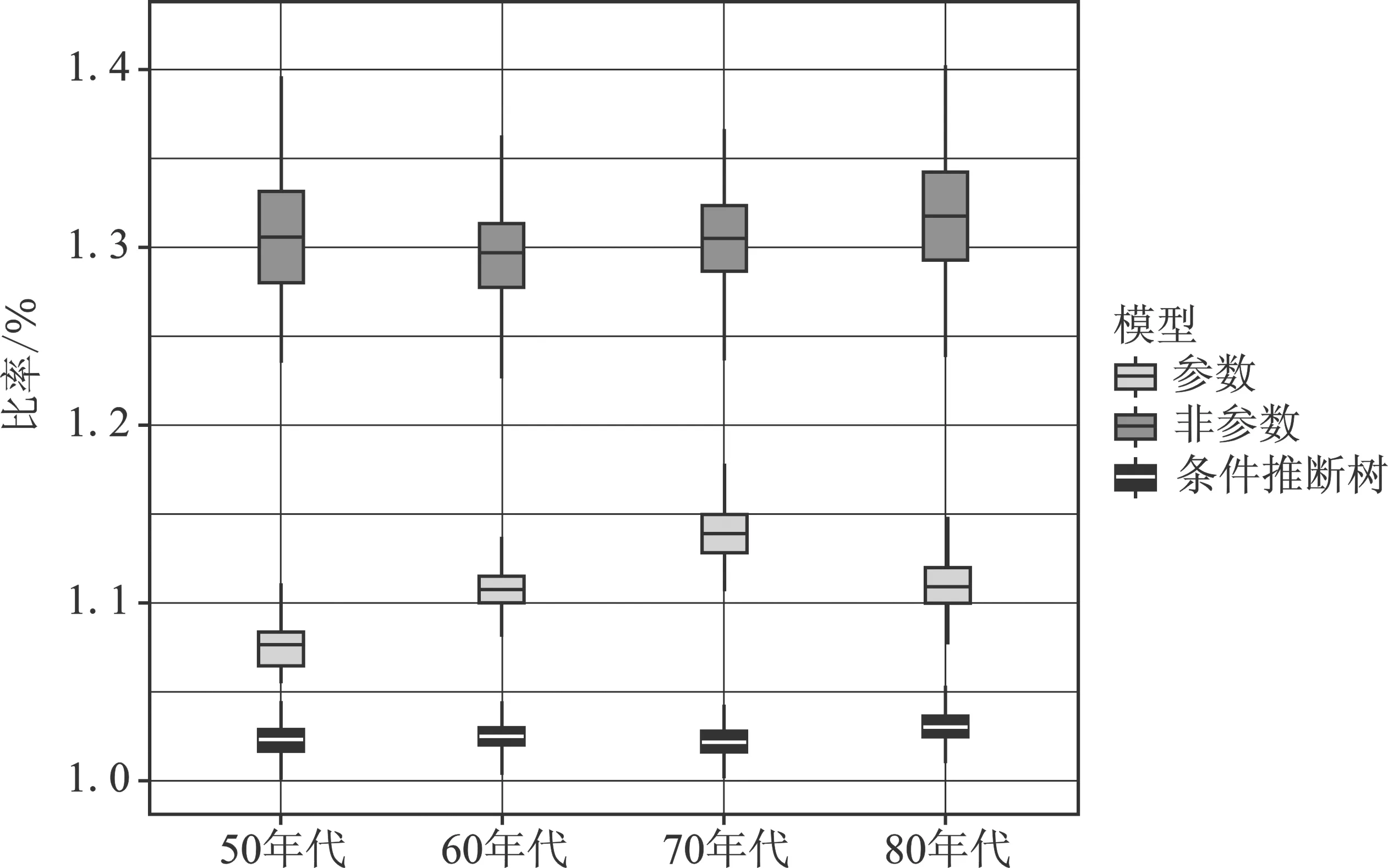
图6 不同测度方法下Ratio箱线图

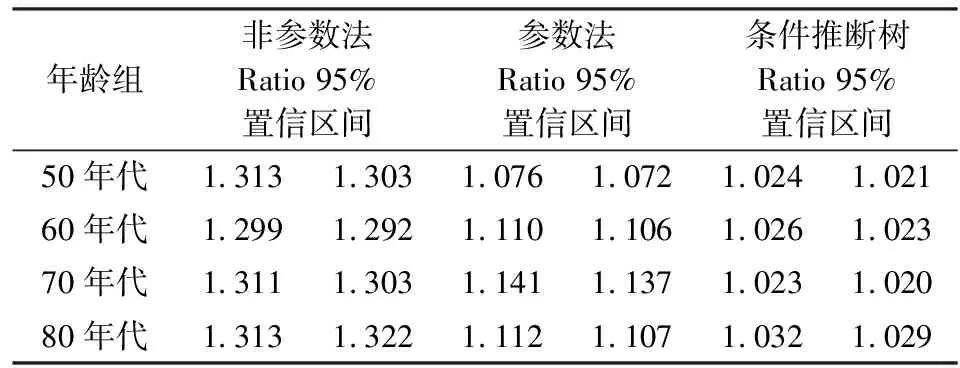
表3 不同测度方法下Ratio 95%置信区间

表4 不同测度方法得到的结果值

六、结论及启示

本文采用回归树模型中的条件推断树和条件推断森林算法来测度机会不平等，均可以降低模型选择过程中个人主观因素影响。通过比较不同模型的样本外检验可以看到，条件推断森林在测试集上的均方误差最小，其次是条件推断树，而非参数法最大，因此条件推断森林可以得到相对更好的机会不平等估计结果。条件推断树在计量经济学意义上并不太复杂，并且提供了方便的图形说明，可直接用于机会结构的分析，同时在机会不平等的估计、环境变量重要性的分配和样本外的表现方面与条件推断森林非常接近。研究发现：各个年代机会树终端节点数目分别为23、33、35、23，环境变量与个体收入之间均存在复杂非线性关系;户口类型是影响“50年代”机会不平等最主要环境变量，“60年代”是性别，“70、80年代”是居住地，且户口类型重要性持续下降，而居住地重要性持续上升；机会不平等的绝对程度由“50年代”的0.129下降到“80年代”的0.049，相对程度由35.3%下降到19.8%。

尽管影响机会不平等的环境变量相对重要性发生了变化，但户口类型、居住地、性别仍然是导致机会不平等最主要的因素，为实现全面小康的发展目标，政府应致力于消除不利环境因素对于机会均等的阻碍：深化户籍制度改革，加快城乡、区域之间基本公共服务均等化；地区之间需要建立一体化劳动力市场，为劳动力跨区域流动创造条件，优化资源配置，减少区域差异对于个体收入的影响；在劳动力市场上为女性创造公平竞争环境，保障女性权益，提供相同的职业流动机会；对外部环境恶劣的贫困人口进行补偿救助，降低教育成本，提高贫困家庭子女进一步教育机会，打破代际之间阶层固化的现象。