组块策略:赋予儿童知识整合的力量
2019-10-15江苏南京市上元小学徐建干
江苏南京市上元小学 徐建干
一、组块策略意义的探索
组块是源于心理学中的词汇,是指将若干较小的单位联合成较大的单位的信息加工。组块是对信息的再加工的过程,也指最后合成的单位。组块概念的提出使得短时记忆的研究得到了重视,现如今在英语和语文等语言类的教学中,通过组块记忆的方式记忆短语和词汇,使得记忆的正确率和效率得到了很大的提升。全国著名特级教师薛法根就一直致力于语文组块教学的研究,并在实践中切实有效地发展了学生的言语智能。数学学习离不开解题,解题能力的高低就与学生头脑中组块数的多少有关。很多数学问题就是由一个数学组块+一个附加条件构成的,如果一个学生对这个数学组块很熟悉,那离解题就是一步之遥了。以组块的眼光审视数学知识点,可以找到其内在的联系,从而完成知识点到知识链再到知识网的搭建过程。
二、组块策略提升解题能力的研究
(一)组块策略在教学中运用的可行性探究
在解决实际问题过程中,往往有一些学生能够很快找到解题思路,而一些学生却难以下手。仔细分析后发现,解题能力强的同学在审题的过程中能够把题目分解为一个熟悉的知识组块+一个附加条件,而解题能力弱的同学缺乏这样的意识,甚至这样的知识组块可能都无法解决,解决这样的问题遇到困难也就在情理之中了。
例如,苏教版数学六年级下册有一道这样的题目:有两支蜡烛,当第一支燃去,第二支燃去时,剩下的部分一样长。这两支蜡烛原来的长度是几比几?这个问题组块是:一个量的几分之几和另一个量的几分之几相等,附加条件是:一支蜡烛用去几分之几还剩下几分之几。在没能完成这道题目的30个同学中,有66.7%的同学是组块问题:一个量的几分之几和另一个量的几分之几相等不能够解决,剩下23.3%的同学是不能把题目分解成组块+一个附加条件的形式,其余的同学则是一点思路都没有。可见在讲解这一道题目的过程中,如果学生不能把一个量的几分之几和另一个量的几分之几相等这一知识组块真正弄懂,则很难真正解决这样的问题。
以组块策略的视角解读学生解决问题过程中存在的问题可以发现,组块掌握的多少、组块掌握的熟练程度关系到问题最后能否顺利解决,以组块的策略解决问题可以帮助学生形成解题思路,找到解决问题中存在的困难。
(二)组块策略在解决问题教学中的运用探究
组块策略在解决实际问题中的运用可以从识别组块和组块训练两个角度来练习。在解决实际问题时,把问题分解成:组块+附加条件的形式以及组块的练习。
例如,苏教版数学六年级下册教材有一道这样的题目:一个圆锥形的沙堆,底面积是24平方米,高1.2米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?首先,分析这道题有两个组块和一个附加条件构成。组块:①圆锥的体积计算,②根据长方体的体积倒推长方体的高度(厚度)。附加条件:圆锥的体积和长方体的体积相等。组块一:圆锥的体积公式是sh,这一题显然运用第二个公式计算。组块二:倒推求长方体的高,长方体的体积公式是V=sh或V=abh,根据体积公式求长方体的高有这样的倒推公式:h=V÷s或h=V÷a÷b。附加条件:圆锥的体积和长方体的体积相等,把圆锥的体积计算出来之后当作长方体的体积。其分析问题的过程从以下流程图来看更清晰(见图1)。

图1
在解决实际问题的过程中,以这样的教学模式去教学引导学生学会分析问题,快速了解自己的知识盲点,查漏补缺。让解决实际问题的练习有方向、有层次、有深度,通过组块练习策略有效提升学生解决实际问题的能力。
三、组块策略提升学习力的教学范式研究
在解决实际问题的过程中运用组块的策略可以帮助学生迅速找到解题思路,而在日常的教学过程中,教师运用组块策略进行教学,则可以从源头帮助学生弄懂知识点之间的内在联系和前后的来龙去脉,夯实基础,实现从知识点到知识链再到知识网的建构过程。
(一)等价条件间的组块替换训练
数学中有一些条件是可以互相等价替换的,通过组块的方式将这些等价条件放在一起替换练习,使学生熟悉从一个条件自由转化为其他条件,再结合具体问题学习根据不同的附加条件选择不同的替换条件。
例如,在学习分数的过程中,关于分率的理解就可以是多角度的。如条件全班男生人数是女生人数的,可以有以下理解:①用份数的方法来理解,把女生人数看作单位“1”平均分成3份,男生人数相当于这样的2份,由此可以得到如图2的线段图,帮助理解;②直接表示为数量关系式——男生的人数=;③反过来看女生的人数是男生人数的;④由第一种理解进一步理解为男生人数占全班人数的,女生人数占全班人数的;⑤复杂的理解还可以得到男生人数比女生人数少;⑥女生人数比男生人数多。如果附加条件是男生人数20人,可以用①②③种中的任意一种替换方式。如果附加条件是全班人数50人,选用①④两种替换方式更简便。如果附加条件是男生比女生少10人,则选用①⑤⑥三种替换法方式更简便。

图2
等价条件间的组块替换训练可以从一道习题的练习过渡到一类题型的练习。熟悉条件的选择和转化,可以使学生通过有限的练习强度实现最完整的学习过程,从而提升学习的效率。
(二)递进知识间的组块对比训练
在学习过程中,对知识点的理解是螺旋上升的,因此随着学习力的逐步提升,一个知识点可能会分散在不同的学段。在小学阶段简便计算就分布在整数范围、小数范围、分数范围以及三个范围的混合计算。下面以两个数的乘法简便计算为例。
整数范围里两个数相乘有两种常见的情况:45×14这种题目的特征就是一个数的末尾是5,另一个数的末尾是双数,可以将双数拆成2乘以一个数,变成45×(2×7),然后变成熟悉的乘法结合律。99×14这种题目的特征就是一个数接近整十整百等数,可以将接近整十或整百的数看成整十或整百的数加减一个数,变成(100-1)×14,然后变成熟悉的乘法分配律。在小数的范围内,同样与整数的两种情况类似,而在分数领域就不存在这样的情况了,因为分数的乘法计算是可以直接进行约分的。然而在分数和整数相乘的范围就有类似的情况,的情况就是分数的分母和整数比较接近,可以把整数拆成分母加减一个数,然后用乘法分配律完成。还有一种就是,这种题目的特征是分数接近整数,可以把分数看成一个整数加减一个分数,同样用乘法分配律来解决。
两位数相乘的简便计算,在不同的范围内既有相同点又有不同点。通过组块训练既可以帮助学生理解知识间的递进关系,通过对比练习又可以避免互相之间的干扰,加深对两位数相乘简便计算的理解,从而提升学习力。
(三)不同板块知识间的组块联系训练
不同的知识板块之间有时也有内在的关联。在学习的过程中,通过组块联系训练可以帮助学生发现不同板块间的隐含关系,从而透过现象看到问题本质上的共通之处。
例如,算式1+2+3+4+5+……可以作为很多问题的列式。在数线段的总数时,以A为左端的线段有AB,AC,AD,AE,AF共5个,以B为左端的线段有BC,BD,BE,BF共4个,以C为左端点有3个……因此可以用上述算式计算。在握手问题中同样存在这样的列式,有6人参加一次聚会,他们之间互相认识,计算握手的次数,以A为起点需要和其他5人握手5次,接着B需要和剩下4人握手……因此也可以用上述列式计算握手次数。在计算南京到苏州单趟火车票车票的总数时,以南京为出发站则终点站可以是镇江、丹阳、常州、无锡和苏州等5站共计5种,以镇江为起始站的有4种车票……因此同样可以用上面算式计算车票总数。除此之外,在数角、数长方形的个数问题中也同样能够用到上面的算式,本质上这些问题都可以归类到第一种数线段的模型中(见图3)。
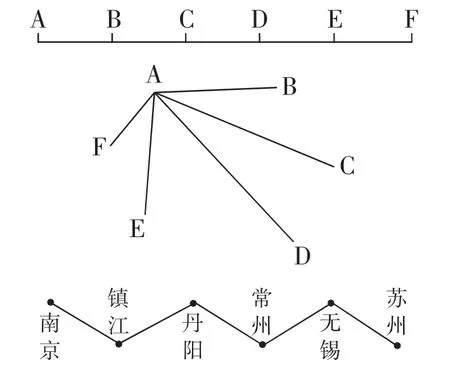
图3
将不同领域却拥有内在联系的知识点作为一个组块来学习,可以帮助学生深刻理解问题背后的本源性知识,不仅知其然,而且知其所以然,达到触类旁通的效果。
组块策略应该是一种教学意识,在教学中通过组块的策略弄懂知识的来龙去脉,知识间的内在联系;组块策略应该是一种学习方式,以组块的视角分析问题,熟悉常见的组块知识,在解决实际问题的过程中以组块为起点思考问题;组块策略应该是一种学习能力,从知识点的掌握到组块的掌握再到组块间的联合,使得学习力螺旋上升。
