修正的响应面方法优化螺栓法兰连接结构几何参数*

2019-10-14蒋国庆陈万华王元兴

国防科技大学学报 2019年5期

蒋国庆，陈万华，王元兴

(中国空气动力研究与发展中心，四川绵阳 621000)

螺栓法兰连接作为火箭箭体级与级之间主要的连接方式之一，其力学性能在很大程度上影响着火箭发射的成败，而其结构质量也在一定程度上影响着射程[1]。以某型火箭为例，若其结构质量减轻1 kg，则射程会增加接近1 km。可见对箭体级间螺栓法兰连接结构开展减重优化是非常必要的。

众所周知，火箭的总质量是相当可观的，其连接部位一般偏向保守设计，导致该处质量偏大，存在较大的优化空间。然而，连接部位结构异常复杂，采用传统的优化方法进行优化计算时，不仅计算效率低，且难以得到最优结果。基于有限元软件的二次开发语言(如Abaqus的Python语言、MSC.Patran的PCL(Patran command language)语言等)得到结构的参数化模型，随后根据响应面方法的基本原理构建结构中所关注的静力学或者动力学响应指标与相关参数之间的响应面模型，再选用遗传算法、模拟退火算法等智能算法对该响应面模型进行优化，这是一种可行的优化思路。蒋国庆等[2]基于PCL语言建立了螺栓法兰连接的参数化模型，并分析了结构刚度对主要几何参数的敏感系数，进而得到了敏感参数和钝感参数。申志彬等[3]基于PCL语言建立了集建模与分析于一体的星形药柱参数化模型，并分析了结构主要几何参数对最大Von Mises 应变的影响规律。万华平等[4]提出了一种基于高斯过程响应面的有限元模型修正方法，相较于传统参数型响应面方法而言，该方法用于有限元模型修正更有优势。鲍诺等[5]基于参数化模型和拉丁方试验设计方法获得了多项式响应面模型，以响应面模型预测结果和实验结果之间的误差为目标函数，并采用自适应模拟退火算法获得了最优的响应面参数，进而得到了修正后的响应面模型，优化后的响应面模型具有良好的复现和预测能力。魏锦辉等[6]提出了基于具有全局收敛特性的自适应响应面的结构有限元修正方法，该方法能够有效避免陷入局部最优，且只需少量样本点即可得到全局最优解。欧阳琦等[7]考虑到响应面方法在并行子空间优化中的不足，提出了基于邻域加强的优化方法，改进后方法的优化效率得到了较大的改善。麻越垠等[8]基于响应面方法对叶栅摆动装置有限元模型的多个参数进行了优化，优化后模型的模态分析结果与模态试验结果之间的相关性得到明显提高。

本文以箭体级间螺栓法兰连接结构的简化模型为研究对象，在综合考虑前述响应指标与优化参数之间的内在联系的基础上，提出一种修正响应面模型。

1 响应面方法

一般而言，螺栓法兰连接结构的参数主要指的是几何参数，设其n个参数分别为x1,x2,…,xn，则其响应y(如位移、应力、加速度等)与参数之间的关系可用式(1)表示：

y=f(x1,x2,…,xn)+ε

(1)

式中：f(x1,x2,…,xn)为响应函数；ε为随机误差，其均值为0、方差为σ2。由式(1)拟合得到的模型称为响应面模型，其预测精度主要取决于f的优劣程度。f一般为多项式，例如二阶多项式，如式(2)所示。

(2)

式中：ai为待定系数，当i≠j时aij表示变量xi和xj两者之间的耦合作用；当i=j时aij表示变量xi的二次效应。

对结构参数进行m次(m≥n+1)设置并分别进行数值计算(以下简称数值试验)，从而可以得到y的m个数值试验值。将这些参数及对应的响应面预测值分别代入式(2)，可以得到如下方程组：

(3)

式(3)的矩阵形式为：

(4)

记这m次试验的数值试验值向量为：

Y=[y(1),y(2),…,y(m)]T

(5)

为使响应面模型的预测误差最小，由最小二乘法有：

(6)

将式(4)代入到式(6)中，可以得到：

δ(A)=(XA-Y)T(XA-Y)

(7)

为使得函数δ(A)取极值，需要满足如下条件：

(8)

对式(8)进行化简，可得

(XA-Y)TX=0

(9)

当XTX不奇异时，可得到A的表达式为：

A=(XTX)-1XTY

(10)

将数值试验值和试验参数代入式(10)即可得到待定系数的值，进而可得相应的响应面模型。

2 修正响应面模型

由式(1)和式(10)可知，响应面模型的预测精度主要取决于响应函数和数值试验。在数值试验相同的条件下，响应函数的选取则显得格外重要[9]。一般而言，多项式响应函数具有一定的普遍性，能够解决大部分拟合问题。在此，把与多项式响应函数相对应的响应面模型称为经典响应面模型。为提高经典响应面模型的拟合精度和预测精度，有时需要多次调整多项式的次数和数值试验的次数。这一过程需要耗费大量的时间和精力。即便如此，有时也不能得到理想的预测精度。因此，需要根据实际情况对多项式响应函数进行一定修正。

经典响应面模型的普适性意味着它与实际案例的关联度不高。因此，对经典响应面模型进行修正时特别需要与具体实际相结合。对螺栓法兰连接结构进行参数优化时，需要根据优化约束条件与优化参数之间的内在联系，建立合理的修正响应面模型。

(a) 实际结构(a) Actual structure (b) 简化结构(b) Simplified structure图1 火箭级间连接结构及其简化结构Fig.1 Connection structure in rocket and its simplified structure

根据火箭箭体级间螺栓法兰连接结构的实际形式(如图1(a)所示)，设计如图1(b)所示简化后的螺栓法兰连接结构(该结构高为700 mm，外径为300 mm)，其中法兰质量主要由内翻法兰宽度t2和内翻法兰厚度t3决定。对法兰进行以质量最轻为优化目标时，若设置约束条件为轴向拉伸载荷作用下顶端位移d不大于某一指定数值，则需要构建该位移与优化参数之间的响应面模型。

为构建合理的修正响应面模型，设计如表1所示数值试验，以获得d与优化参数之间的内在联系，表中t2和t3的单位均为mm，下同。

根据数值试验一的计算结果，可得d与优化参数之间的关系曲线如图2所示。

由图2可知，内翻法兰宽度t2与模型顶端轴向位移之间近似为二次函数关系，内翻法兰厚度t3与该位移之间近似为倒数关系。令x1=t2、x2=t3，设计修正响应面模型为：

(11)

与之相对应的经典响应面模型为：

(12)

为求得式(11)和式(12)中的未知数，根据均匀试验原理设计得到表2所示数值试验，计算结果见表2。

(a) 内翻法兰宽度t2(a) Width of flange t2

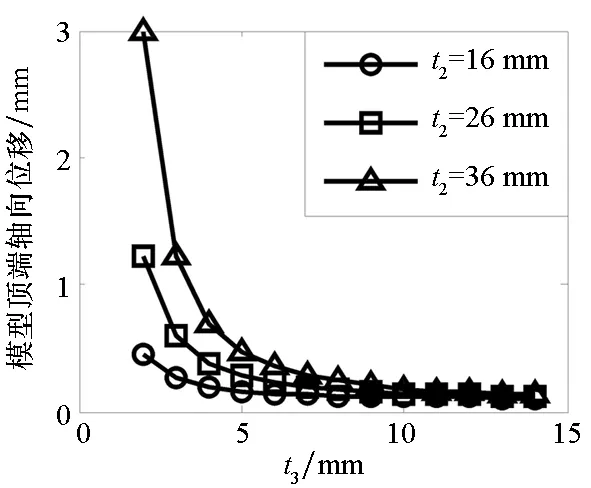
(b) 内翻法兰厚度t3(b) Thickness of flange t3图2 顶端位移d与优化参数关系曲线Fig.2 The curve between d and parameters

表1 数值试验一

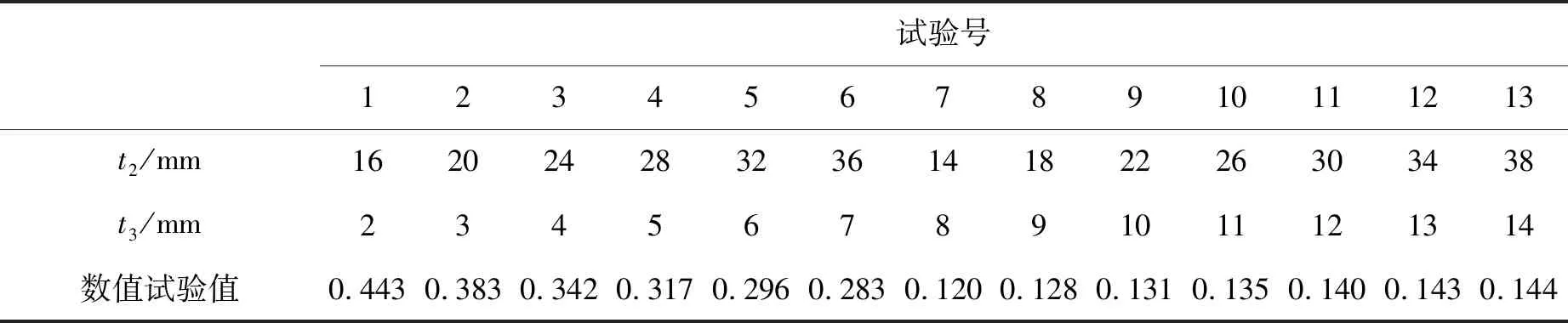
表2 数值试验二

根据表2的相关数据，可计算得到修正响应面模型和经典响应面模型分别为：

(13)

d=0.059 0+0.035 5x1-0.181 1x2-

(14)

与式(14)相比，式(13)中其余项的系数远小于0.000 1，在此忽略不计。式(13)和式(14)所对应的曲面分别如图3和图4所示。

图3 经典响应面Fig.3 Typical response surface

图4 修正响应面Fig.4 Modified response surface

为对比两个模型的预测精度，重新设计数值试验并统计计算结果如表3所示。采用式(13)和式(14)分别对数值试验进行预测，把预测结果和预测误差也统计于表3。

由表3可知，修正响应面模型的预测值误差相对比较均匀，且最大误差绝对值要明显小于经典响应面模型的相应值，最大误差为7.55%。因此，对螺栓法兰连接结构进行参数优化时，可以优先考虑修正响应面模型。

3 螺栓法兰连接结构参数优化

对螺栓法兰连接结构进行参数优化时，设置其优化目标为法兰质量最轻，取法兰密度为ρ=2.7×10-9t/mm3，则法兰质量为：

(15)

式中，Mflange的单位为t。

考虑到现有的螺栓法兰连接结构模型是根据现有经验设计而得，在给定载荷(即50 kN集中拉力)作用下模型顶端轴向位移为0.14 mm。因此，可将该值设置为约束条件之一。综合考虑参数的可变范围，可得螺栓法兰连接结构的优化模型为：

(16)

采用遗传算法对式(16)进行参数优化计算，其中种群数设置为50，迭代次数设置为40，优化过程如图5所示。由图5可知，当迭代次数为15时，已经得到优化结果，统计如表4所示。

表3 数值试验三

图5 修正响应面模型优化计算过程Fig.5 Optimization process of the modified response surface model

x1/mmx2/mmMflange/kg优化前26101.096优化后14.006.700.424变化幅度/%-46.15-32.96-61.36

由表4可知，法兰质量得到大幅度减小，取得了较为理想的优化结果。为验证优化结果的有效性，利用优化后的参数，建立优化后的螺栓法兰连接结构模型的有限元模型并进行相同拉力载荷下的静力学分析，得到模型顶端轴向位移为0.13 mm。该位移值与目标位移相差-7.14%。即优化后的法兰结构不仅质量得到了大幅度减小，且模型的抗拉刚度得到一定增强，所以优化效果是非常明显的。