高中数学中条件最值的求法探究
2019-10-14辽宁省盘锦市辽东湾实验高级中学赵盼盼
数学大世界 2019年22期
辽宁省盘锦市辽东湾实验高级中学 赵盼盼
条件最值是指在某些约束条件下的最值。在大学数学中,对于多元函数在约束条件下的最大(小)值,常用拉格朗日乘数法,先求条件极值,再具体判断该条件极值是否是所求的条件最值。在高中数学中,学生并未学习到拉格朗日乘数法,但这并不表示某些条件最值在高中阶段不能解答。下面通过例题介绍条件最值在高中数学中常用的解题方法。


【总结】 本题是把求最值的函数进行变形,然后利用常数代换。常数代换时对条件又进行了简单变形,目的是使乘积为定值。
例2 若正数x,y满足x+4y=xy,求x+y的最小值。

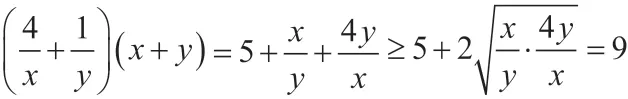

故此函数的最小值是9。


故此函数的最小值是9。
【总结】 解法一是将条件灵活变形,利用常数代换的方法构造和或积为常数的式子,然后利用均值不等式求最值;解法二是消元法,即根据条件建立两个量之间的函数关系,将条件最值转化为无条件最值,然后代入代数式转化为函数的最值求解。
解:因为x>0,y>0,所以,当且仅当x=3y时等号成立。
设x+3y=t>0,则t2+12t-108 ≥0,所以(t-6)(t+18)≥0,
又因为t>0,则t≥6。故当x=3,y=1 时,x+3y的最小值是6。
【总结】 本题中是对条件使用均值不等式,建立所求目标函数的不等式求解。
本文通过例题讲解了在高中数学中求条件最值的三种方法,其中,均值不等式起到了很大的作用。应用均值不等式时,一定要注意不等式成立的条件“一正、二定、三相等”。在求解条件最值问题时,掌握有效的变形技巧,可以培养学生的数学能力。
