一种面向球姿态检测的图像透视畸变校正方法
2019-10-11王媛媛
刘 坚 王媛媛
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
0 引言
由于相机成像模型自身的局限性会使图像产生“近大远小”的透视畸变,在对物体进行几何尺寸和空间位置的视觉测量时严重影响测量精度,因此校正图像的透视畸变对于提高视觉测量精度至关重要。目前校正图像“近大远小”透视畸变的方法主要分为两类:通过得到物体的理想正视图图像的校正方法和透视误差补偿的校正方法。其中通过得到物体的理想正视图图像的校正方法是使物体目标平面上的点与相机平面的距离相等来实现的[1],主要有角度检测法、控制点变换法和射影几何方法[2]三类,这些方法都基于旋转角度检测和直线检测技术,算法比较复杂[3]且应用范围有限,仅对平面物体的图像具有较好的校正效果,对于曲面物体其理想正视图中物体上的点与相机平面的距离并不相等,仍然存在“近大远小”的透视畸变,因此无法应用到曲面物体的图像透视畸变校正中。透视误差补偿的校正方法[4]直接对待测物体的像在标定平面逆映射的等效物理尺寸进行误差补偿,但需要已知待测物体与标定平面的准确距离。
在机械制造领域,圆形或球形特征的物体十分常见,对于这类物体,一般需采用双目视觉方法,借助多个视图获取三维实体的参数。当物体的特征模型已知时,通过物体的单视图也能检测物体的三维位置和姿态,其中最常见的是利用物体与其投影图像之间存在的特定的点、线对应关系求解其三维位置[5]。本文的检测目标是实现对一带有圆形特征的球体的空间姿态测量,环绕该球体球面大圆处有一条凹槽,该凹槽构成了一个空间圆环,而空间圆在摄像机像平面上所成的像是椭圆形[6],因此该凹槽在像平面上所成的像是半个椭圆,若球体及凹槽的形状参数是已知的,则可以通过球体的单视图图像中椭圆的参数检测其当前姿态[7]。但是由于透视畸变的存在,球体凹槽上的点离相机平面的距离均不相同,导致其在图像平面的椭圆的投影中心误差[8]、长轴误差和短轴误差很大,大大降低球体姿态的检测精度。
针对上述问题,本文基于逆透视畸变[9-10]和摄像机标定技术[11-12]提出了一种面向球姿态检测的图像透视畸变校正方法。
1 相机成像基本理论
理想的相机成像模型为平面透视投影模型,即小孔成像模型,该模型是目前摄像机标定和机器视觉中应用最广泛的模型[13]。其成像原理如图1所示,其中坐标系OwXwYwZw为世界坐标系,用来表示被拍摄物体和相机在空间中的位置;坐标系OcXcYcZc为相机坐标系,Oc为相机的光心,Zc坐标轴与相机的光轴重合;坐标系Oixy为图像坐标系,原点Oi为光轴OcZc与图像平面的交点,称为图像主点,x轴平行于Xc轴,y轴平行于Yc轴;OtUV为像素坐标系,以像素为单位。
空间中任意一点M(xw,yw,zw),在相机坐标系中的坐标可以通过旋转矩阵R和平移矩阵T变换得到,即世界坐标系和相机坐标系之间的变换关系为
(1)
建立相机坐标系和图像坐标系之间的变换关系:
(2)
其中,K为相机的内参数矩阵;(u0,v0)为图像主点的像素坐标;f为相机透镜的焦距;dx、dy分别为x轴、y轴方向单位像素的物理大小。内参数矩阵K、旋转矩阵R、平移矩阵T都可通过相机标定获得。
但这种相机成像模型存在不可避免的缺点,在同一张图像中,物体“近大远小”的现象造成的畸变直接影响视觉测量精度,图1中线段MN和线段PQ实际长度相等,且平行于图像平面,根据透视投影原理可得,物距较小的线段PQ在相平面上的投影大小明显大于物距较大的线段MN的投影,这就是本文中主要研究的透视畸变,而这种透视畸变在光心附近较小,远离光心处逐渐变大。

图1 相机成像模型Fig.1 Camera imaging model
2 针对球姿态检测的透视畸变校正方法
2.1 球体姿态检测
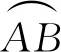

图2 待检测球体模型Fig.2 Tested sphere model
2.2 基于逆透视变换的图像透视畸变校正算法
逆透视变换为上述透视变换的逆过程,是为了找到图像上点的像素坐标与其世界坐标之间的对应关系,从而可以恢复空间中某一平面的部分信息。
由式(1)、式(2)可知,若已知K、R、T的值,可由物体上的点的空间坐标(xw,yw,zw)得到图像上对应的像素坐标,但由现实三维空间的点转换为二维图像坐标后,丢失了深度信息,若能够已知物体上点的三维坐标中的某一维,则可完成图像上点的像素坐标(u,v)到空间三维坐标(xw,yw,zw)的转换。因此可将要恢复的空间平面的z坐标均设为0,从而得到空间平面x、y坐标信息,这就是逆透视变换的过程[14]。
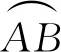
由此可知P平面上点的世界坐标(xwP,ywP,0)与像素坐标(uP,vP)之间的关系为
(3)
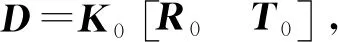
(4)
由于球心在P平面上,由上式可得球心的世界坐标。
Qi平面上点的世界坐标(xwQ,ywQ,zwQ)与像素坐标(uQ,vQ)之间的关系为:
(5)
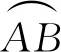
(6)
其中(a,b,c)是由式(4)计算得到的球心的世界坐标,zwQ的值等于di,OR为球体半径。
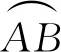
3 实验
3.1 实验方案
实验方案如图3所示,旋转台和旋转摆角器连接共同完成绕Z轴方向和绕Y轴方向的转动,将球体放置于旋转台中心,使球心与摆角器的摆角中心重合,且球心位于相机光轴附近,相机和旋转台的初始位置均与水平面平行,光源采用平行背光源和两个条形光源,保证球体外轮廓和球面细节清晰,通过光源控制器调节光源的亮度,为避免环境光的干扰,实验在暗箱中进行。实验开始后,相机和光源的位置均保持不变。

图3 实验模型Fig.3 Experimental model
完成不同角度的球体图像采集后,将球体从旋转台上取下,并将摆角器的角度恢复到初始位置,相机焦距和位置均不改变,然后用精密标定板对相机进行标定实验,并对过球心且垂直于相机光轴的平面位置进行标定。
图4为依据实验方案搭建的实验平台,实验装置包括精密光学平台、型号为piA2400-17gc的Basler彩色CCD相机、GCM-730402M型旋转摆角器、GCM-1101M型旋转台、OPT-FAT50型平行背光源、OPT-LXT402221型条形光源、OPT-DPA1024E-4型光源控制器、Win7 64位系统工控机、带有水平仪的相机支架、棋盘格边长为5 mm且图案阵列为12×9的标定板,以及3D打印的球体,该球体打印精度达到0.1 mm,球体直径60 mm,在球体最大圆处有一个深度为1 mm、宽度为0.5 mm的凹槽,球下方为定位结构,保证球心位于转台中心且凹槽所在的平面初始位置垂直于旋转平台。
3.2 实验步骤
(1)利用SolidWorks设计球体模型,并将模型导入3D打印机中,调节打印参数,打印出符合精度要求的球体。
(2)调整实验平台,首先利用相机支架上与相机相连接的水平仪将相机调平,使相机平行于水平面,然后将旋转台和摆角器均调至0°,将球体放置于旋转台并固定,使球心与摆角器的摆角中心重合,且球心位于相机光轴附近,此时α和β都等于0°。
(3)采集球体不同α和β的图像,在拍照过程中保持光源不变,相机焦距不变,通过调整旋转台和摆角器的角度获取球体不同姿态。
(4)完成球体图像采集后,取下球体,进行标定实验。将旋转台和摆角器均调至0°,然后将标定板放置于过球心且垂直于相机光轴的平面位置,对标定板进行拍照,以便得到相机相对P平面的外部参数;最后调整标定板的姿态,得到15~20张不同角度的标定板的图像,完成标定实验。
4 实验结果分析与讨论
4.1 本文算法流程
本文算法流程如图5所示,首先由采集的标定板不同角度的图像计算得到相机的内部参数、外部参数和畸变系数,然后对采集的球在不同姿态的每张图像进行如下操作:
(1)根据求得的相机畸变系数对采集的球的图像进行几何畸变校正。
(2)利用图像预处理、边缘提取和Hough变换[15]等方法拟合球的外圆并求得球心的像素坐标,再根据相机内部参数和相对P平面的外部参数计算得到球心的世界坐标。
(3)提取球面上凹槽所形成的弧线,为了提高透视畸变校正算法的效率,选取弧线上部分像素点进行透视畸变校正,得到其校正后的像素坐标。
(4)利用透视畸变校正后的像素点进行椭圆拟合,得到α、β的值。
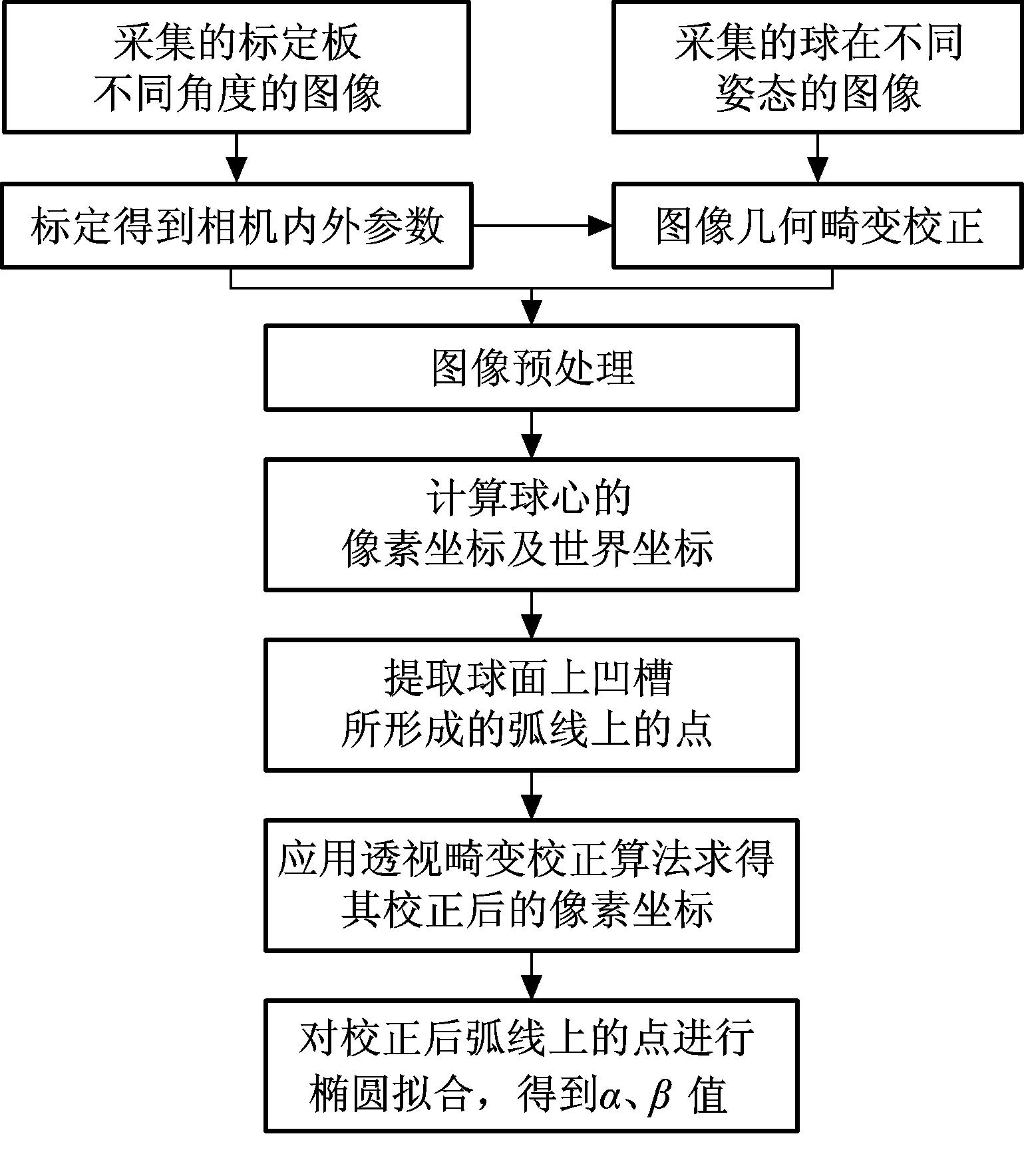
图5 本文算法流程图Fig.5 Flow chart of the method
4.2 算法对比
文献[4]中通过建立透视投影误差模型对齿轮廓圆的“近大远小”透视畸变进行了校正,其透视投影误差的非线性数学模型如下:
(7)
其中,L0为待测物体在标定平面内的实际长度;S0为标定平面到相机镜头的工作距离;ΔS为待测物体离标定平面的距离;f为相机的焦距。
应用该算法的流程如下:首先对原始图像中提取的球面凹槽形成的弧线进行椭圆拟合,计算出短轴逆映射到标定平面后的等效长度;然后根据逆透视变换计算得到球面弧线上与短轴相交的点离标定平面的距离,以此代表短轴离标定平面的距离;最后应用式(7)中的误差补偿模型对椭圆短轴进行误差补偿。由于该算法是直接对椭圆短轴长度进行误差补偿,因此只能校正α,而β的值与校正前相等。
4.3 实验数据

图6 采集的原始图像Fig.6 Collected original image

图7 弧线校正的图像Fig.7 Arc correction image

图8 未校正和校正后椭圆拟合结果图Fig.8 Pre-correction and post-correction ellipse fitting results
图6为α=40°、β=-1°时采集的原始图像。图7为应用本文算法对弧线进行透视畸变校正的图像,图中弧线是直接提取的凹槽所形成的弧线,标记点是对弧线上的部分像素点进行透视畸变校正后的像素点位置,图8所示为应用本文算法前后对弧线进行椭圆拟合的结果,图中外侧椭圆为校正前的拟合结果,内侧椭圆为校正后的拟合结果,从图中可以看出校正后的椭圆短轴长度明显小于校正前的椭圆短轴长度,正是由于球体的外轮廓圆所在的平面距离相机较远,凹槽形成的弧线距离相机较近,将弧线上的点全部平移到外轮廓圆所在平面后再次透视投影,短轴长度会变短。
4.4 数据分析与讨论
表1为β理论值为-1°、α理论值为5°~50°时未进行透视畸变校正、应用本文算法和文献[4]的算法进行透视畸变校正计算得到的α和β值的对比。从表中可以看出,在未进行透视畸变校正时计算得到的α误差很大,最小误差为1.499°,最大误差达到了9.210°,平均误差为5.912°,且误差随着其角度的增大也逐渐增大,这正是由于“近大远小”透视畸变造成的,位于光轴附近的图像透视畸变较小,而离光轴较远的图像透视畸变较大,实验数据验证了透视畸变这一特点。未进行透视畸变校正时β的最小误差为0°,最大误差为4.642°,平均误差为1.019°,由此可见

表1 透视畸变校正前和透视畸变校正后计算的角度(β=-1°)Tab.1 Angle before and after perspective distortion correction (β=-1°)(°)
透视畸变对α的影响最大,而对β的影响较小,这是由于β是由椭圆长轴的倾角决定,而椭圆长轴两端始终在同一平面上。
图9为根据表1数据得到的应用本文算法校正后α的绝对误差趋势图,平均误差为0.563°,与校正之前相比精度有了很大提升,并且误差值随α的变化随机波动,但当α=50°时,误差明显较大,这是由于相机景深是一定的,此时椭圆弧线距离初始对焦的位置远大于景深,导致获取的图像模糊,弧线位置提取不准确,使得误差明显增大。应用本文算法校正后β的平均误差为0.372°,精度有了明显提高。

图9 本文算法校正后α的绝对误差趋势图(β=-1°)Fig.9 The absolute error trend of alpha angle after correction by the method (β=-1°)
应用文献[4]的算法校正后α的平均误差为1.143°,与校正前相比精度有很大提升,但与本文算法相比,α理论值为10°~50°时其校正精度均低于本文算法的校正精度,只有在α理论值为5°时其精度略高于本文算法的校正精度,这是由于应用文献[4]的算法时,误差补偿值主要由短轴在标定平面的等效长度及短轴到标定平面的距离决定,因此由球的图像拟合的椭圆短轴的精度和β的精度严重影响其最终的校正精度,而在α较小时,透视畸变也较小,由球的图像拟合得到的椭圆短轴长度和β误差都很小,导致α较小时其精度较高。而当α较大时,拟合的椭圆误差也较大,其校正精度较低。由于该算法只能对视觉测量中待测物体的长度进行透视畸变校正,因此并不能对β进行校正,适用范围较小。
为了进一步验证算法的稳定性和有效性,分别计算了不同β值时的球的不同姿态。表2、表3、表4分别对应β理论值为1°、5°、-5°,α理论值为5°~50°时的数据。从表中可以看出,应用本文算法校正后α的平均误差均在0.6°以下,其精度高于应用文献[4]算法校正后的精度,证明了本文算法的先进性。图10、图11、图12分别为根据表2、表3、表4数据得到的应用本文算法校正后α的绝对误差趋势图。
应用本文算法校正后的角度检测误差主要来源是由实验装置带来的系统误差和图像处理过程中弧线提取不准确带来的随机误差。光学平台表面的加工误差和安装误差可能导致其平面并不水平,相机和实验球体安装过程中的误差可能导致初始位置球心、摆角器的摆角中心和相机光轴没有在同一直线上等,这些由于实验装置制造和安装过程中引入的误差都是系统误差;球体最大圆处的圆形凹槽宽度为0.5 mm,深度为1 mm,采集的图像中凹槽所形成的弧线具有一定的宽度,因此在图像处理过程中提取弧线的中心位置的像素点时会带来随机误差。

表2 透视畸变校正前和透视畸变校正后计算的角度 (β=1°)Tab.2 Angle before and after perspective distortion correction (β=1°)(°)

表3 透视畸变校正前和透视畸变校正后计算的角度(β=5°)Tab.3 Angle before and after perspective distortion correction(β=5°)(°)
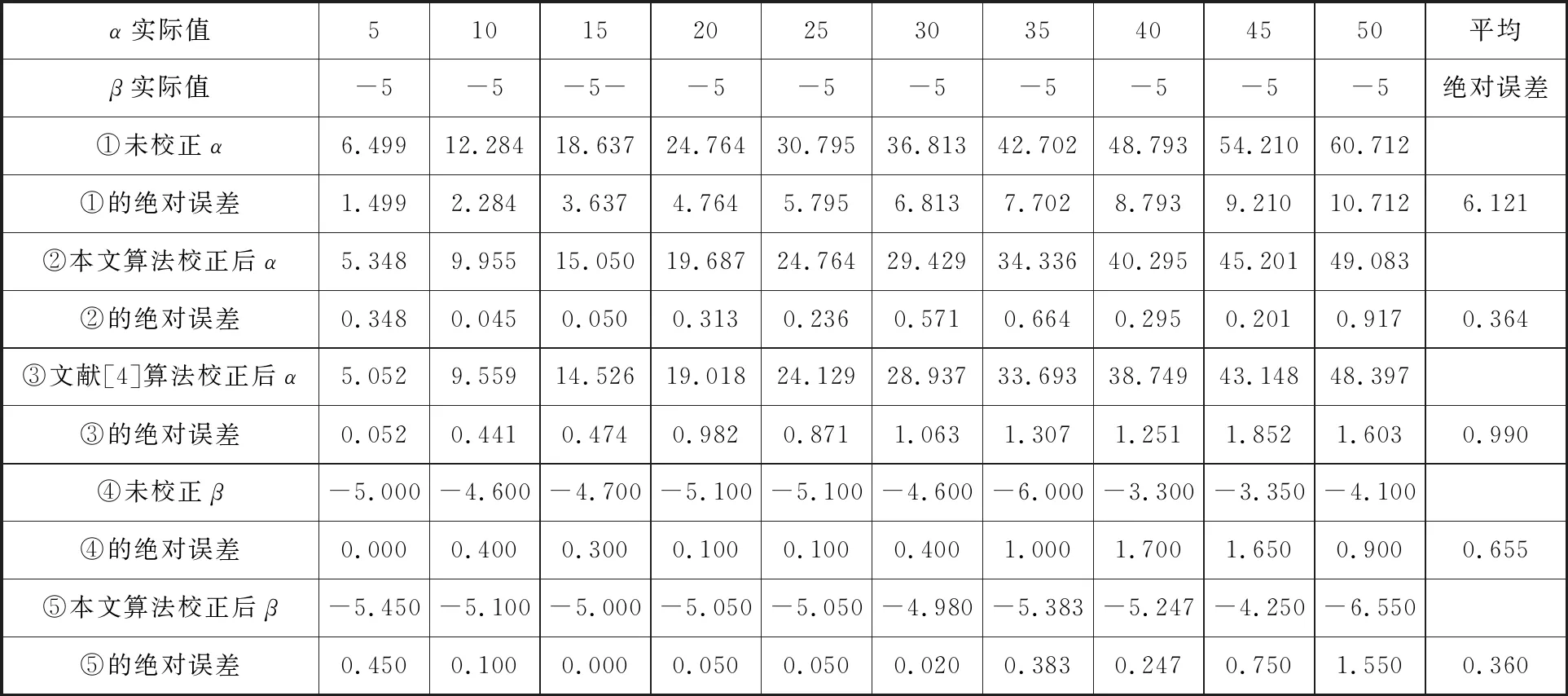
表4 透视畸变校正前和透视畸变校正后计算的角度(β=-5°)Tab.4 Angle before and after perspective distortion correction (β=-5°)(°)

图10 本文算法校正后α的绝对误差趋势图(β=1°)Fig.10 The absolute error trend of alpha angle after correction by the method (β=1°)
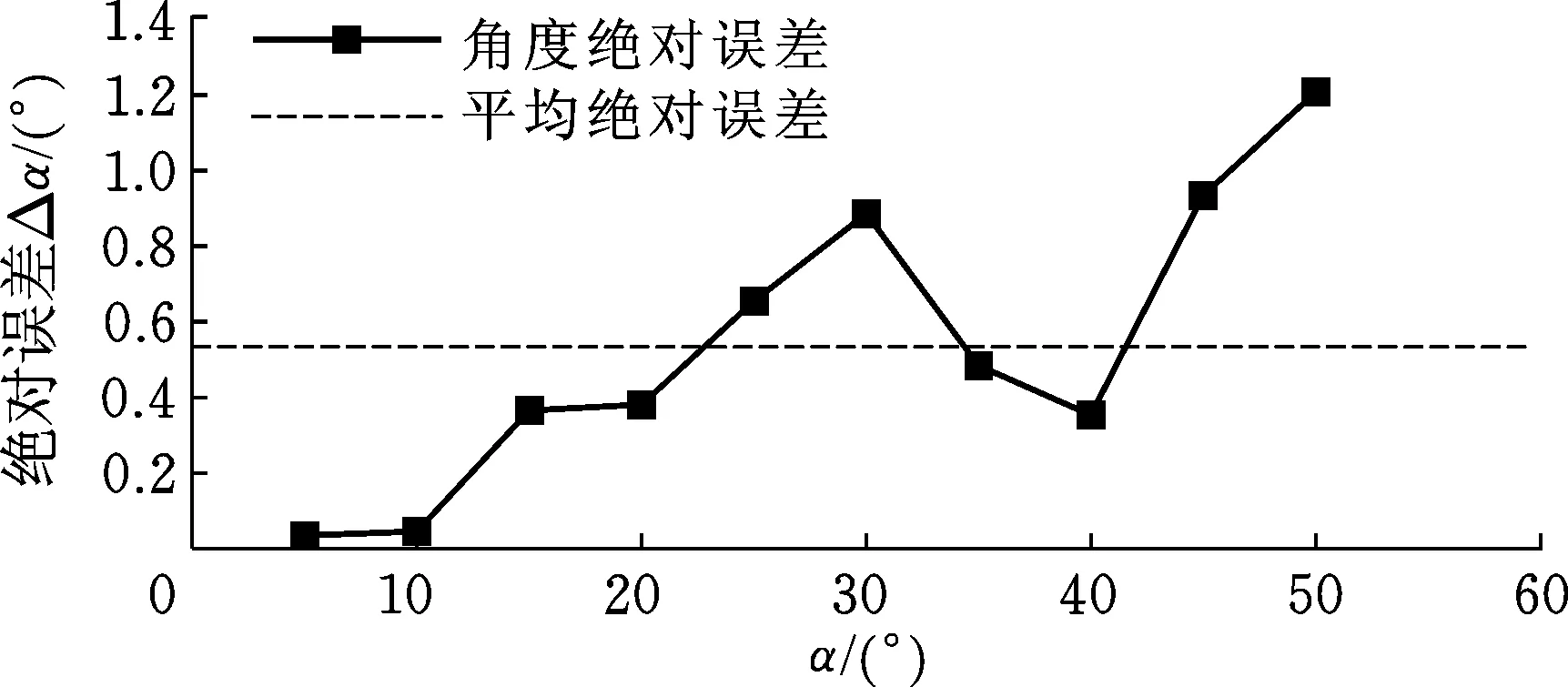
图11 本文算法校正后α的绝对误差趋势图(β=5°)Fig.11 The absolute error trend of alpha angle after correction by the method (β=5°)

图12 本文算法校正后α的绝对误差趋势图(β=-5°)Fig.12 The absolute error trend of alpha angle after correction by the method (β=-5°)
5 结论
(1)本文基于逆透视变换理论提出了一种面向球姿态检测的图像透视畸变校正方法并从理论上分析了其可行性,详细介绍了图像透视畸变校正方法的步骤;与现有的透视畸变校正算法进行对比,本文提出的图像透视畸变校正方法在球姿态检测中对α和β的测量精度更高,能够满足工业生产中对球姿态的测量需求。
(2)本文提出的图像透视畸变校正方法应用范围广泛,可以应用在具有圆形特征或球形特征物体的视觉检测中,为视觉测量领域提供了一种更高精度的图像透视畸变校正方法。
