HSI颜色空间下的直线导轨表面缺陷检测方法
2019-10-11周友行马逐曦石弦韦
周友行 马逐曦 石弦韦 孔 拓
湘潭大学机械工程学院,湘潭,411105
0 引言
直线导轨作为支撑和导向的高精密零件,会由于表面加工缺陷而导致定位精度下降、使用寿命缩短。采用机器视觉技术进行导轨表面质量检测可解决缺陷微小、加工现场干扰强,以及离线式人工抽检带来的检测质量不稳定的问题。
基于机器视觉的表面缺陷检测的关键在于待处理图像的颜色空间表征、高维数据特征信息的获取、多层特征信息的混合优化。国内外学者对此进行了大量研究。马云鹏等[1]使用邻域灰度差对图像进行分割处理,利用主成分分析(principal component analysis,PCA)进行图像降维和融合。蔡蕾等[2]使用稀疏性非负矩阵分解,对加工缺陷的时频图像进行降维和识别。WEI等[3]利用PCA将RGB空间中各分量矩阵进行降维,建立不均匀照明模型,通过优化模型得到缺陷分割图像。VALAVANIS等[4]通过Sauvola局部阈值处理和基于图形的分割方法,将图像具有大变化的特征提取出来,实现缺陷的分割。ABDEL-QADER等[5]提出了基于PCA的裂缝提取算法,将灰度图像分为多个子块,对每一个子块进行裂缝线性结构建模,使用PCA对子块进行降维和融合。DHARMAGUNAWARDHANA等[6]提取RGB图像中各分量的信息,构建9维颜色特征向量,采用PCA将全特征向量降维成25维特征向量,进一步改善了对区域边界的确定,并完成彩色图像分割。上述方法都是基于RGB颜色空间的图像缺陷提取。由于相同灰度无法在RGB颜色空间中有效映射出唯一颜色,颜色改变时RGB三个分量的值都会产生变化,光照不均时无法体现亮度的区别等原因,因此,缺陷提取时,RGB颜色空间对背景纹理的干涉较为敏感,容易将背景纹理误判为缺陷提取出来。
HSI颜色空间则弥补了RGB颜色空间的不足,使用色调(hue)、饱和度(saturation)和亮度(intensity)三个分量描述颜色。目前,国内外学者在农田图像分类[7]、面部识别[8]、建筑材料识别[9]和钢索防锈涂层的识别[10]等领域展开了大量的研究,并取得了非常好的效果。HSI颜色空间中,人眼感知的色差与颜色数值之间的欧氏距离成正比,色调、饱和度和亮度具有独立性,颜色信息与亮度信息分离,HSI颜色空间表征的图像与人类对图像的解读方式更为一致,因此在视觉检测时,常采用HSI颜色空间表达图像信息。但在HSI空间中使用单一分量描述图像无疑会损失了其他分量包含的信息,降低了图像的区分度;若将图像的多个分量加权混合计算,则不仅计算量巨大,而且各分量图像所占权重也无法确定。
为了解决上述矛盾,本文将RGB颜色空间的直线导轨表面图像转换为HSI颜色空间的图像,并提取饱和度和亮度的颜色信息,采用主成分分析法将分量特征降维,利用粒子群算法优化其相应的加权系数,得到最优效果混合灰度图像,继而获取二值图像,完成缺陷特征提取。
1 实验设计与图像采集
根据直线导轨常用材质和加工工艺要求,本文将70 mm×70 mm×20 mm的45钢和15钢的矩形工件作为待加工工件,模拟直线导轨表面平面铣削加工过程。
如图1所示,采用天准VMU222影像仪采集划痕、凹坑、烧伤、锈斑等常见的金属表面缺陷(图2)。采集的图像模式为RGB,图像分辨率为256 pixel×256 pixel,图像在实际工件中的采集面积为2.291 2 mm×2.291 2 mm。

图1 图像采集中心Fig.1 Image acquisition center

图2 直线导轨表面缺陷Fig.2 Surface defects of linear guide
对4幅图像依次进行表面缺陷的人工定量检测。测量方法:根据原始图像计算缺陷所占像素个数,通过换算得到实际的缺陷的长、宽、面积和影响区域。表1中,实际影响区域为缺陷最大宽度与缺陷总长度之比。

表1 表面缺陷人工测量结果Tab.1 Results of surface defects by manual measurement
注:图2a有2个缺陷,“/”前后的数据是2个缺陷的数据。
2 颜色空间原理及转换
颜色空间是颜色在三维空间中的排列方式。为了满足不同场合的需要,人们构造出多种颜色空间,其中,RGB空间是最基础的颜色空间。RGB空间是三维直角坐标系统中的一个单位正方体,红色(R)、绿色(G)、蓝色(B)三个通道按不同比例叠加形成各种颜色,如图3所示。

图3 RGB颜色空间Fig.3 RGB color space
HSI空间是双圆锥上的圆柱坐标系,以人眼视觉特征色调、饱和度和亮度来描述颜色,如图4所示。色调描述颜色属性,用圆锥横截面圆的角度表示。饱和度描述颜色的鲜明程度,用与圆锥中心轴的距离表示,轴上各点饱和度为0,锥面上各点饱和度为1。亮度是指颜色明暗程度,用圆锥中心轴的距离表示,下部圆锥顶点0,逐渐变到上部圆锥顶点1。

图4 HSI颜色空间Fig.4 HSI color space
RGB空间到HSI空间的转换关系为

(1)
(2)
(3)
式中,R、G、B分别为红、绿、蓝的分量;H、S、I分别为色调、饱和度和亮度的分量。
从RGB空间到HSI空间的转化是非线性变换,将R、G、B颜色分量用色调、饱和度和亮度信息独立表示。亮度与彩色信息无关,色调、饱和度与人感受颜色的方式息息相关,因此,HSI颜色空间类似于人眼对颜色特性的感知,更适合于进行缺陷检测的图像处理。
3 算法实现
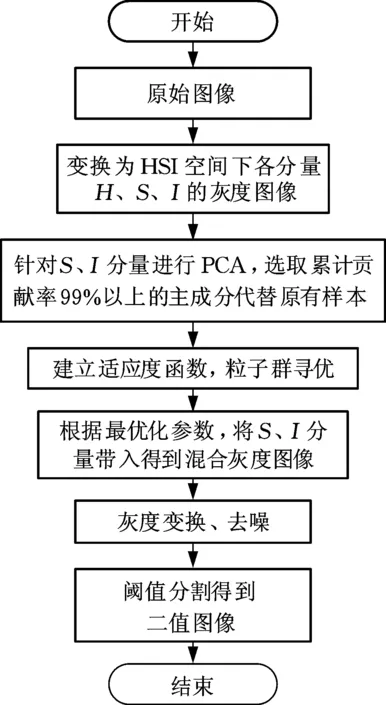
图5 算法流程Fig.5 Algorithm flow chart
首先将表面缺陷原始图像从RGB空间转化到HSI颜色空间,得到HSI分量灰度图像;再基于PCA方法对各分量灰度图像进行降维处理,去除特征间的冗余信息;之后,利用粒子群算法优化其相应的加权系数,混合饱和度和亮度的灰度图像,得到最优效果;最后通过阈值分割得到缺陷的二值图像,提取出直线导轨表面缺陷。我们选取图2a为本节例图。具体实现过程如图5所示。
3.1 空间变换及混合图像矩阵构建
根据式(1)~式(3),将原始图像从RGB空间转换到HSI颜色空间,得到直线导轨表面图像色调、饱和度与亮度的各分量灰度图像(图6)。

图6 表面缺陷HSI颜色空间分量图Fig.6 HSI color space component diagram of surface defects
由图6可以看出,导轨表面饱和度、亮度的图对缺陷和背景纹理表达清晰,色调图虽然能体现缺陷,但背景纹理部分信息混乱,对缺陷干扰较大。人眼对亮度的敏感程度远远强于颜色浓淡的敏感程度,因此混合饱和度、亮度的分量图提取缺陷。
针对饱和度、亮度的灰度矩阵构建混合灰度矩阵模型:
V=[(E-S)α1+Iα2]/β
(4)
式中,E、S、I分别为单位矩阵、饱和度矩阵和亮度矩阵;α1、α2、β为控制常数。
3.2 主成分分析法图像降维
根据式(4),我们使用优化算法寻找最优加权系数α1、α2、β,以弥补通过个人主观感觉和经验确定加权系数造成的误差。本文使用的样本图像分辨率为256 pixel×256 pixel,如果直接进行寻优混合,会产生65 536维向量,导致运算量大、效率低,因此先使用主成分分析法进行降维处理。
主成分分析可将高维数据投影到低维空间,并尽可能多地保留原始信息中的有用信息,极大地减小了计算的复杂度和难度。
将N幅分量图看作数据集X=[x1x2…xN],其中,列阵xi表示第i幅图像(图像分辨率为mpixel×npixel),则图像维度M=mn。
计算数据集X的协方差矩阵:
(5)
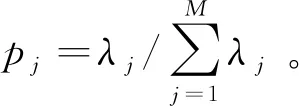
累计贡献率大于99%即可完整表达饱和度、亮度的原始图所含信息,从而得到投影矩阵
Y=XTs
(6)
式中,特征空间s表示累计贡献率大于99%的前d个最大特征值对应的特征向量组成的矩阵。
PCA降维处理后的图像见图7。

图7 表面缺陷S、I分量降维图Fig.7 S &I component dimension reduction of surface defects
使用PCA进行数据的降维,一方面可以使样本的信息量降低,计算量减小;另一方面,当数据受噪声影响时,最小的特征值对应的特征向量往往和噪声有关,降维可以在一定程度上对混合灰度图像起到去噪的效果。经过降维的图像(图7)不仅完整保留了缺陷信息,而且去除了明显的走刀痕迹,抑制了背景纹理对缺陷提取的干扰。
3.3 基于粒子群优化算法的图像混合
根据上一节的降维结果,利用粒子群算法的寻优能力[11-12],以降维后的饱和度、亮度的分量图作为初始图像,按照式(4)进行图像混合。
为衡量混合效果,本文首先构造适应度函数。引入先验条件互信息
(7)
式中,φYV为原始图像与混合灰度图像的互信息量;pV(k)、pY(k)分别为混合灰度图像和原始图像的灰度概率密度;pYV(k,i)为原始图像和混合灰度图像的联合灰度概率密度。
表征混合图像从原始图像中获得的信息量。
互信息量越大,表示混合的图像质量越好,因此选取最大互信息量,构建适应度函数:
max{|φYV|}
(8)
结合适应度函数和混合灰度图像公式,首先将粒子群随机初始化,即将粒子i的位置矩阵Zi和初始速度Vi设置为M×N维的零矩阵;之后,根据式(8)计算每个粒子的适应度,同时选择每个粒子的当前最好位置和粒子群全局最好位置。
粒子i的速度和位置的更新计算公式为
Vi(t+1)=Vi(t)+c1r1(Pbest,i-Zi(t))+c2r2(Gbest,i-Zi(t))
(9)
Zi(t+1)=Zi(t)+Vi(t+1)
(10)
式中,Vi(t+1)、Zi(t+1)分别为第i个粒子在t+1次迭代时的速度和位置;c1、c2为学习因子;r1、r2为区间[0,1]中的随机数;Pbest,i为当前个体极值;Gbest,i为当前群体极值。
更新之后,重新计算适应度。对于每个粒子,若当前适应度优于Pbest,i的适应度,则替换原来的Pbest,i;继续将粒子当前的适应度与Gbest,i的适应度比较,若优于Gbest,i,则将当前适应度作为Gbest,i。当迭代次数等于200时,算法结束。图8为优化后的混合灰度图。

图8 表面缺陷混合灰度图像Fig.8 Mixed gray image of surface defects
将混合灰度图像进行灰度变换、锐化和去噪等处理后,缺陷与背景的对比度增强,缺陷信息更明显,背景纹理弱化。最后,将后处理的图像使用阈值分割将缺陷信息提取出来。阈值T范围是{(T≤0.4)∪(T≥5)}。阈值分割结果如图9所示。

图9 表面缺陷二值图像Fig.9 Surface defect binary image
4 试验结果与分析
采用HSI空间下直线导轨表面缺陷提取方法对图2所示的4种缺陷进行提取,效果如图10所示。

图10 直线导轨表面缺陷二值图像Fig.10 Surface defects binary image of liner guides
为衡量本文算法提取效果,结合RGB空间下的提取算法(采集图像灰度化→灰度图像阈值分割→二值图像),选取同一幅原始图像进行对比实验。实验分为两个步骤:①结合表1所示的人工测量结果,从缺陷的形状、位置等进行对比,以评价对缺陷和背景纹理的定性判断;②从提取缺陷的准确度来进行对比,以评价算法的有效性。
图2所示4张图片的测量结果如表2所示,可以看出,与人工测量结果对比,HSI空间下提取的缺陷较为准确,而RGB提取的缺陷受背景纹理的影响,测量参数出现了较大的误差。
误分率是一种现今较为常用的图像分割性能测试标准[13],其表达式为
(11)
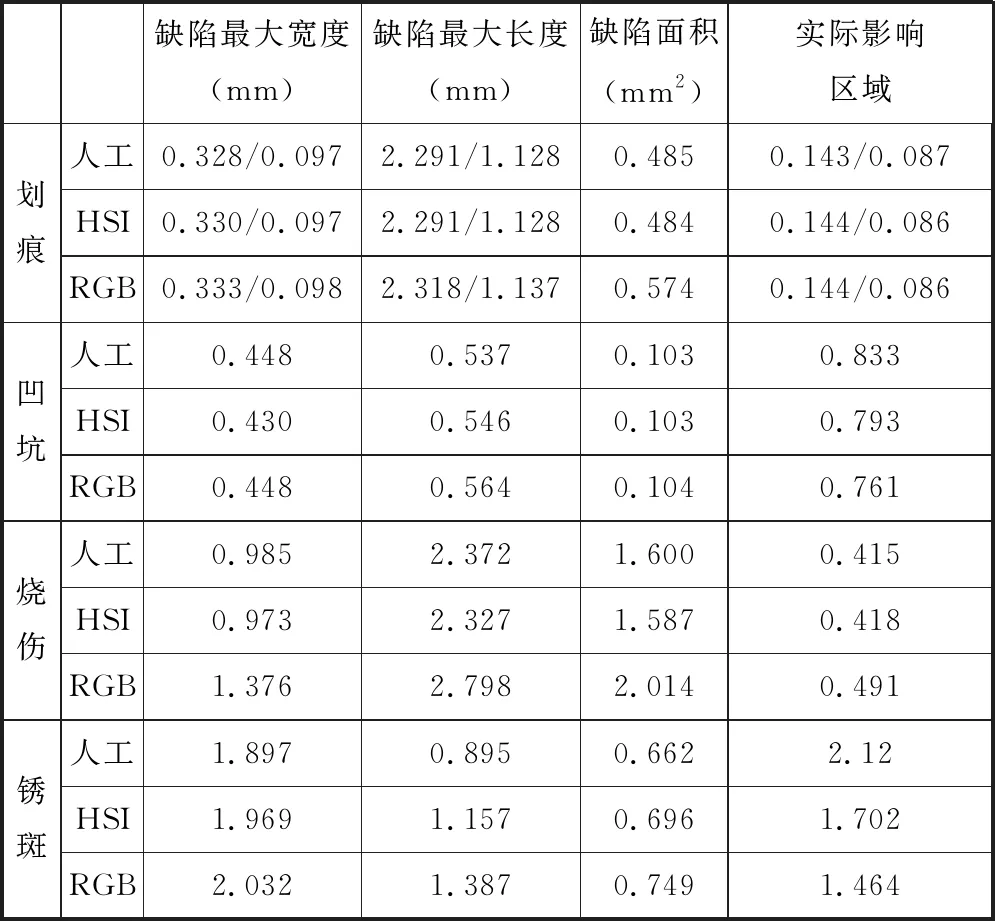
表2 提取缺陷参数对比Tab.2 Results of extraction defect parameters
式中,BO与FO是标准二值掩码(ground truth)图像中背景纹理与缺陷,是由人工观察制作而成;BT与FT为提取后二值图像的背景和缺陷;∩为取交操作;|*|表示*所代表图像的像素点个数。
根据式(11)将缺陷区域看作图像前景,将直线导轨表面无缺陷区域看作图像背景进行计算,得到各颜色空间下缺陷分割结果的误分率γ。γ是背景像素被错误划分到前景区域的比例,或前景像素被错误划分到背景区域的比例,γ越小,提取效果越好。计算结果见表3。
表3 不同缺陷的误分率
Tab.3MEofdifferentdefects
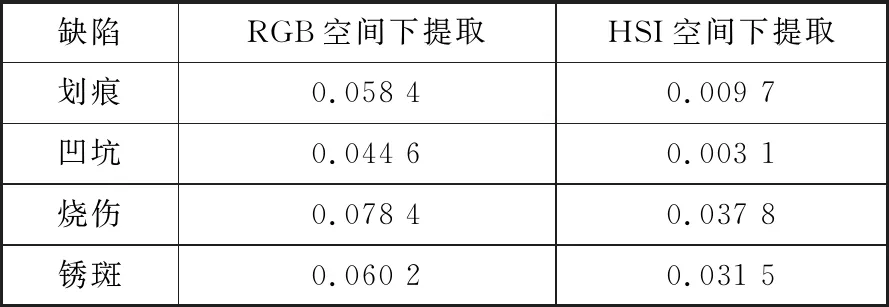
缺陷RGB空间下提取HSI空间下提取划痕0.058 40.009 7凹坑0.044 60.003 1烧伤0.078 40.037 8锈斑0.060 20.031 5
从表3中可以看出,HSI空间下提取时γ较小,而RGB空间下提取时γ较大,这证明同一幅图像在HSI颜色空间下的处理效果更好。
为验证该算法的稳定性,我们从样本库的500张含缺陷图像中随机抽取20张图像,分别使用本文方法和RGB空间下提取方法计算γ,并统计20张图像的γ的均值。重复抽取20次,记录每次20张图像的γ的均值。如图11所示,对比20次计算所得γ可知,本文算法的γ比RGB空间下提取方法的γ平均小5%,由此证明本文算法的稳定性和有效性。
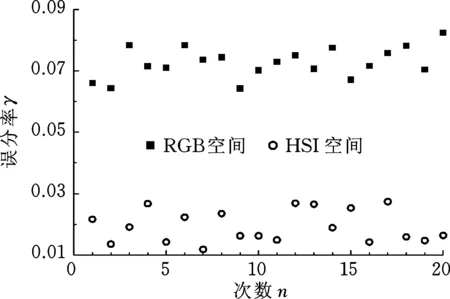
图11 算法稳定性Fig.11 Algorithm stability
5 结论
(1)图像从RGB空间通过非线性变换转化到HSI颜色空间后,可以将彩色信息与亮度信息分开,从多个特征上表示缺陷和背景信息,弥补了RGB颜色关联性大的问题。
(2)饱和度、亮度的分量灰度图完整保留了图像的缺陷和背景纹理信息。通过主成分分析对高维饱和度、亮度的分量图进行降维,并使用粒子群算法优化降维后的饱和度、亮度分量混合灰度矩阵模型的加权参数,实现对直线导轨表面缺陷的提取处理,弱化了背景纹理对缺陷提取的干扰,得到了较为准确的缺陷信息。
(3)将缺陷外形和准确度作为标准,采用本文方法与RGB颜色空间下的缺陷提取方法对4种类型缺陷图像进行比较,本文方法能更好地判断缺陷外形和位置,弱化背景纹理的干扰,测量结果与人工测量结果基本吻合;对比不同类型缺陷的处理结果可知,本文算法的缺陷分割误分率均有明显减小。从样本库中随机抽样20次,本文算法提取处理后的误分率比RGB空间下提取结果的误分率平均减小5%,从而证明了本文算法的有效性和稳定性。
