偏转板伺服阀前置级结构参数优化研究
2019-10-11刘文可陈奎生湛从昌
刘文可,陈奎生,湛从昌,张 磊,吴 凛
(1. 武汉科技大学机械自动化学院,湖北 武汉,430081;2. 武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081)
电液伺服阀是伺服控制系统的关键性元件,通过给它输入电压或电流信号获得液压信号,其性能决定电液伺服系统的可靠性、灵敏度 、控制精度等[1-3]。偏转板伺服阀与射流管伺服阀结构类似,其采用质量较小的偏转板移动代替了射流管摆动,提升了前置级响应速度,抗污染性好,结构更为简单,但其前置级流场复杂,而且在偏转板加工时,多采用电火花及线切割加工,工艺也较复杂。邢晓文等[4]分析了不同形状导流口对前置级性能的影响,得到前置级采用矩形导流口工作时性能最好;蒋大伟[5]研究了喷嘴宽度、偏转板V形导流槽夹角和劈尖宽度对前置级动静态特性的影响;刘志会等[6]根据射流级约束,结合优化算法,实现了射流级的优化设计;张硕文[7]通过AMESim仿真,研究了偏转板射流伺服阀冲蚀前后对空载流量和主阀芯位移的影响;鲁远[8]建立了偏转板伺服阀的系统数学模型,对伺服阀动态特性进行了分析;Shang等[9]对前置级结构进行研究得到,增大偏转板射流伺服阀射流管的喷口宽度和减小喷口的导流长度有利于提高阀的性能;朱海军[10]运用FLUENT软件分析前置级流场,得到了一种解决偏转板伺服阀失效无法对中问题的方法。
目前对偏转板伺服阀劈尖高度和V形槽下端喷口导流长度等结构参数优化的研究有待进一步深入,本文通过分别改变这两种结构参数建立新的前置级模型,利用ICEM和FLUENT软件分析前置级流场静态特性;对前置级的流量曲线进行二次拟合,建立偏转板伺服阀数学模型,利用SIMULINK模型进行动态仿真,分析偏转板伺服阀系统的动态特性,从而优化偏转板伺服阀前置级结构参数,以期为偏转板伺服阀设计提供参考。
1 偏转板伺服阀结构及工作原理
偏转板伺服阀是一种二级电液伺服阀,主要由马达组件、前置级和滑阀组成,其中前置级包括偏转板和射流盘,其结构示意图如图1所示。图1中,喷嘴通过电火花工艺加工在射流盘上,劈尖两侧开有左右接收孔;偏转板上端连接弹簧管,下端连接反馈杆,反馈杆插入滑阀上加工的凹槽中,同时偏转板上开有成一定角度的V形槽。
偏转板向右移动时前置级油液的流动示意图如图2所示。从图2(a)中可以看出,当伺服阀未得电时,偏转板处于射流盘中位,高压油从喷嘴射出流经V形槽被劈尖分流,一部分从偏转板下端面与射流盘形成的间隙中流向泄油口,一部分流入左右接收孔,作用于滑阀,此时左右接收孔流入的油液流量相同,在滑阀左右两端面形成的压力也相同,因此滑阀处于零位。从图2(b)中可以看出,当伺服阀得电由衔铁组件产生的力矩促使偏转板向右移动时,流入右接收孔的流量超过左接收孔的流量,右接收孔的压力大于左接收孔的压力,从而形成一个促使滑阀向左滑动的压差力。当滑阀向左滑动时,阀口打开,控制着流量压力的输出,同时反馈杆下端的小球在滑阀凹槽中跟随滑阀运动,使反馈杆产生形变,形成反作用力,使其流量压力输出达到稳定。
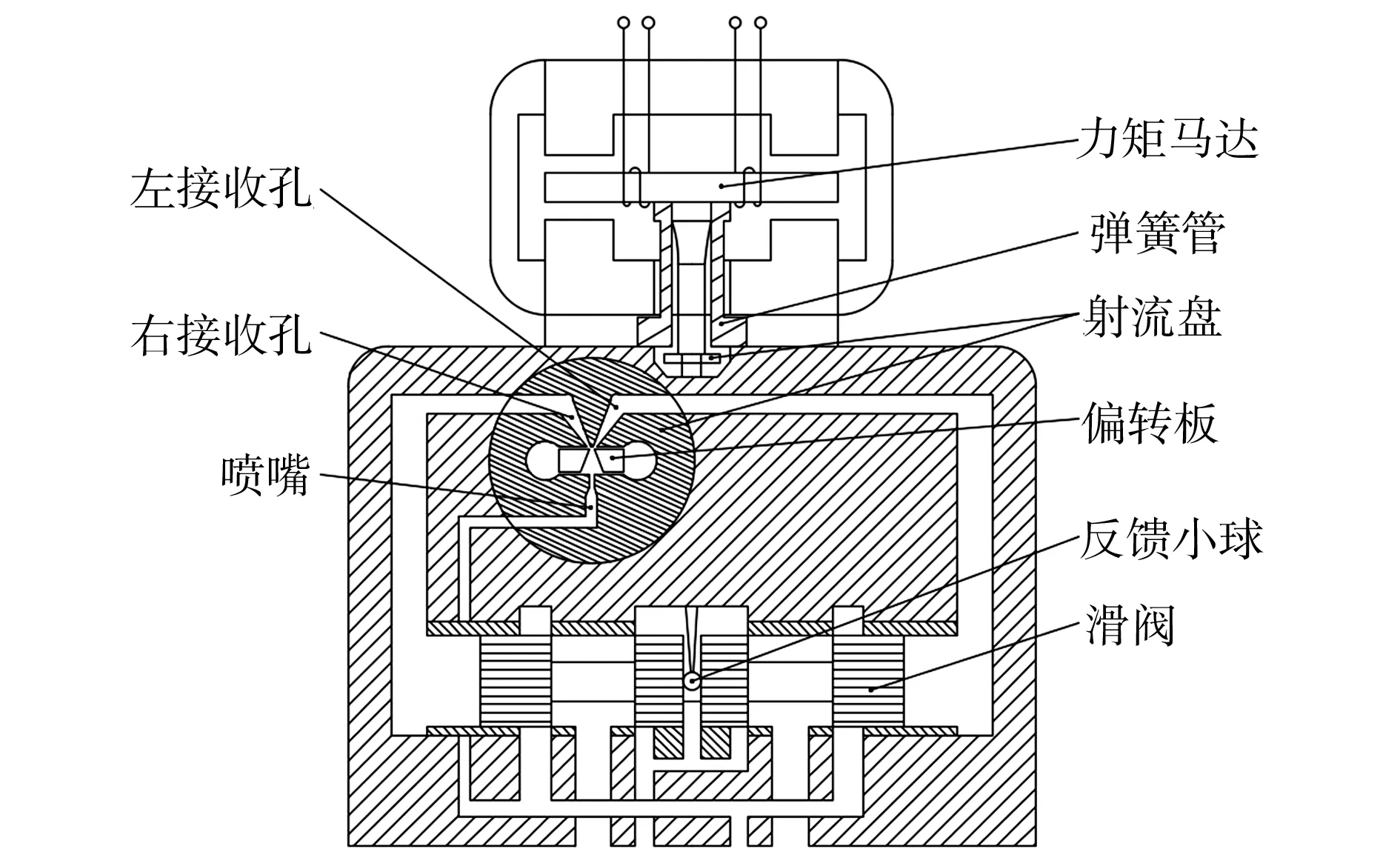
图1 偏转板伺服阀结构示意图
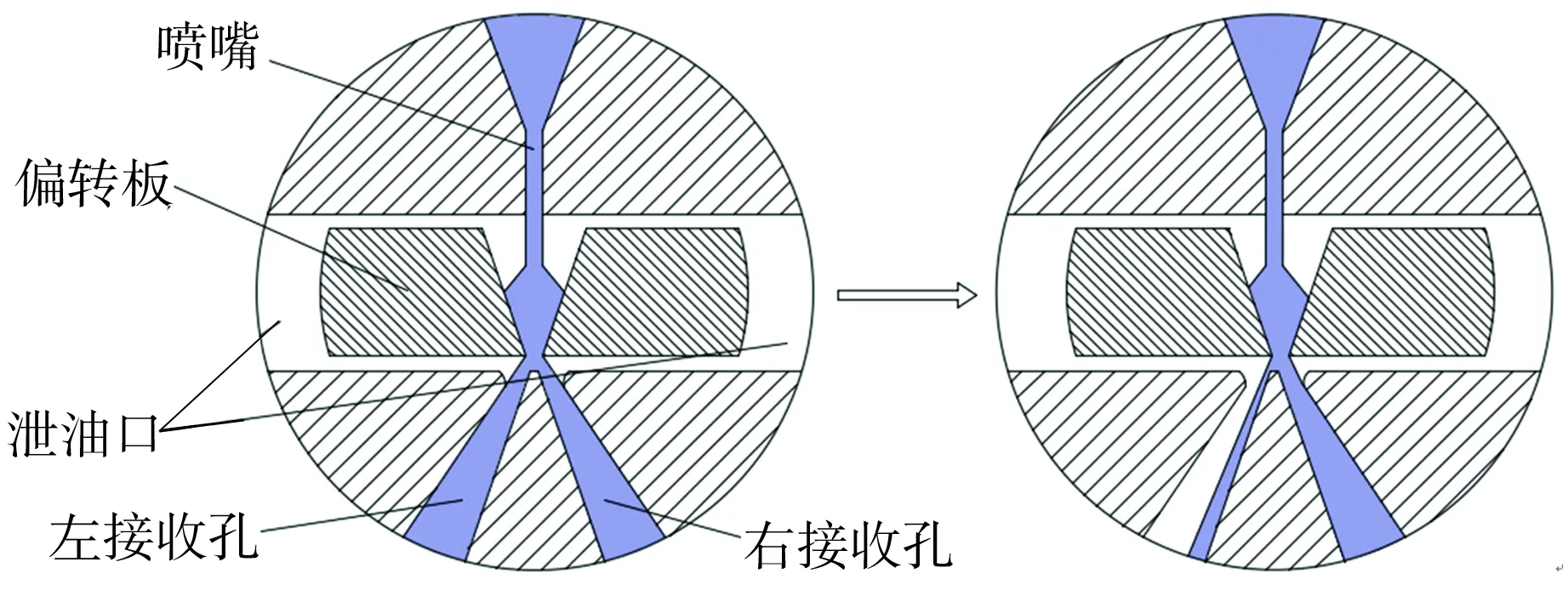
(a)偏转板在中位 (b)偏转板右移
图2 偏转板向右移动时前置级油液的流动示意图
Fig.2 Schematic diagrams of pre-stage oil flow when the deflector moves to the right
2 偏转板伺服阀前置级流场建模
2.1 前置级流场模型
偏转板伺服阀前置级主要结构参数如图3所示,其中喷嘴宽度为0.155 mm,喷嘴锥角为41°,喷嘴导流长度为0.4 mm,喷嘴口端面到偏转板上端面的距离为0.2 mm,偏转板厚度为0.51 mm,偏转板V形导流槽夹角为37°,V形导流槽下端喷口宽度为0.155 mm,偏转板下端面到接收孔端面的距离为0.2 mm,接收孔处圆角半径为0.2 mm,左右接收孔两圆角圆心的距离为1.08 mm, 左右接收孔内侧夹角为38°,外侧夹角为68°,劈尖宽度为0.1 mm。
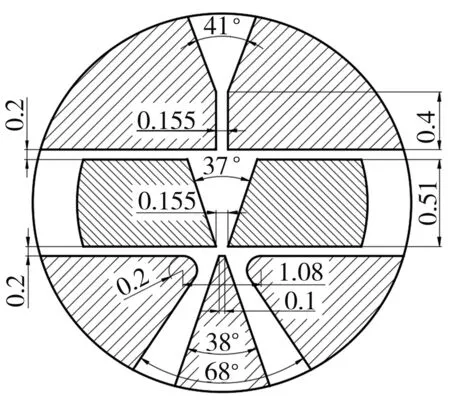
图3 偏转板伺服阀前置级主要结构参数图
Fig.3 Main structural parameters of pre-stage of deflector servo valve
根据前置级的主要结构参数,利用SolidWorks软件并参考文献[5]创建前置级流场的压力和流量三维模型如图4所示。
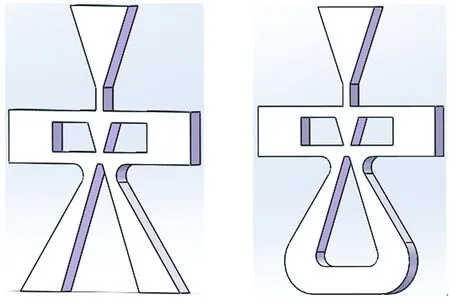
(a)压力模型 (b)流量模型
图4 前置级流场的压力和流量三维模型
Fig.4 3D models of pressure and flow in the pre-stage flow field
2.2 网格划分及流场边界条件设置
将导入ICEM中的几何模型进行块生成、切块、关联、剖分、节点设置等生成结构化网格,前置级流场的压力和流量结构化网格模型如图5所示。将生成的mesh文件导入FLUENT进行求解和后处理。偏转板伺服阀工作时,前置级液压油处于高速高压状态,内部流动十分复杂,采用RNGk-ε湍流模型求解,湍动能系数和湍流耗散率均设置为 1.39。运用标准壁面处理条件进行初始化[11]。将压力油入口定义为压力入口边界,压力值为21 MPa,压力油出口定义为压力出口边界,压力值为0.3 MPa,压力油密度为850 kg/m3,运动黏度为0.031 Pa·s,为保证精度,设置各项残差收敛数值为10-5。左右接收孔对称位于劈尖两侧,当偏转板向右偏移时,同时监测左右接收孔的压力,左接收孔的压力就等同于偏转板向左偏移时右接收孔的压力。
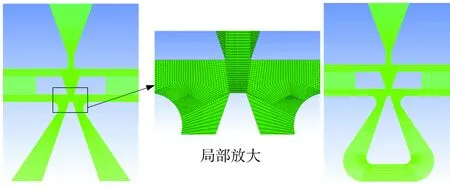
(a)压力模型 (b)流量模型
图5 前置级流场的压力和流量结构化网格模型
Fig.5 Structured grid models of pressure and flow in the pre-stage flow field
3 偏转板伺服阀前置级流场仿真分析
3.1 流场仿真
图6为偏转板向右偏移分别为 0、0.02、 0.04 mm 时前置级压力模型的压力云图。从图6中可以看出,随着偏转板向右偏移,左接收孔压力不断减小,而右接收孔压力不断增加;偏转板处于中位时,在V形槽下端喷嘴两侧出现负压带;随着偏转板向右偏移,V形槽下端喷嘴左侧负压带区域逐渐扩大,而右侧负压带区域逐渐缩小。
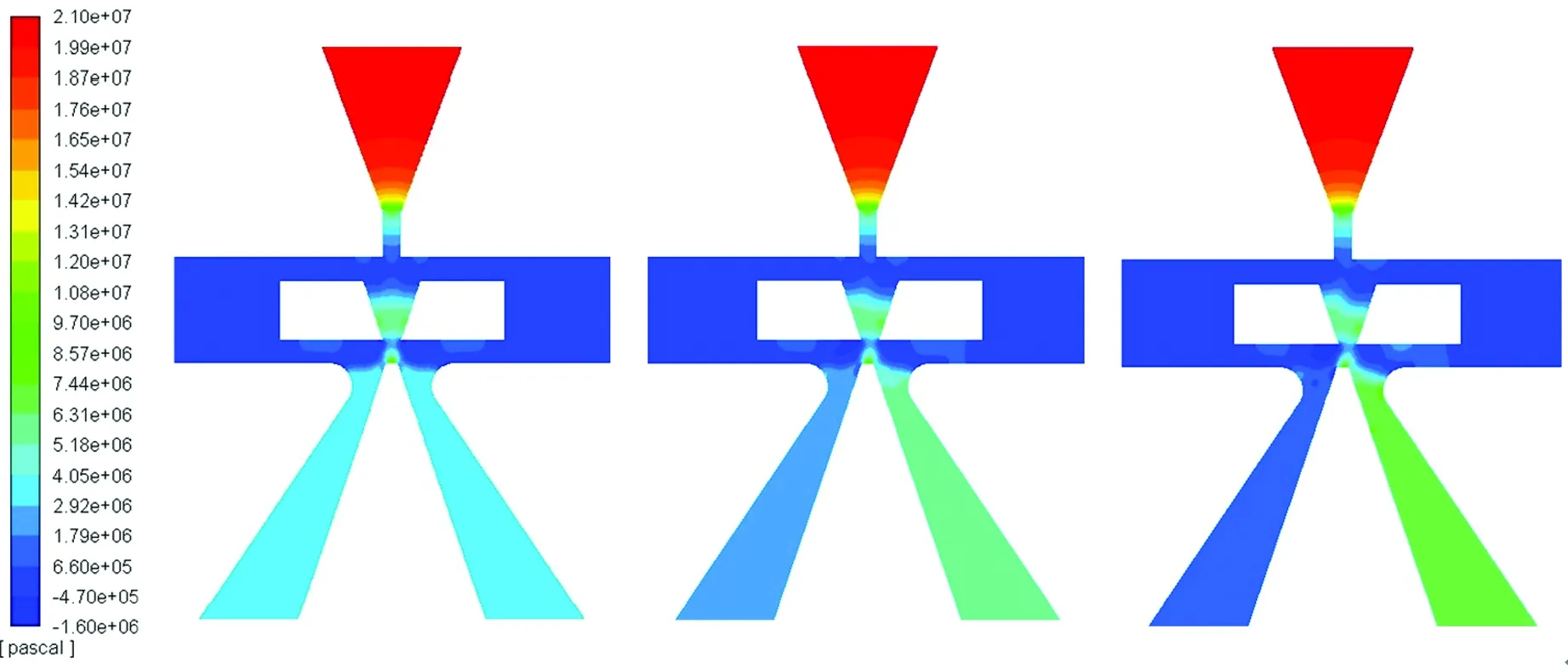
(a)无偏移 (b)偏移0.02 mm (c)偏移0.04 mm
图6 偏转板向右偏移时前置级压力模型的压力云图
Fig.6 Pressure contour diagrams of pre-stage pressure model when the deflector moves to the right
图7为偏转板向右偏移分别为 0、0.02、 0.04 mm时前置级的速度矢量图。从图7中可以看出,随着偏转板不断向右偏移,V形槽下端喷出的油液更多地流向右接收孔,而流向左接收孔的油液逐渐减少;在偏转板处于中位时,流入左右接收孔的油液相同;随着偏转板向右偏移,更多的油液从偏转板下端与左接收孔之间的间隙流出,这是由于流入右接收孔的油液多,且流速大,从接收孔下端流向左接收孔,然后从左接收孔流出。
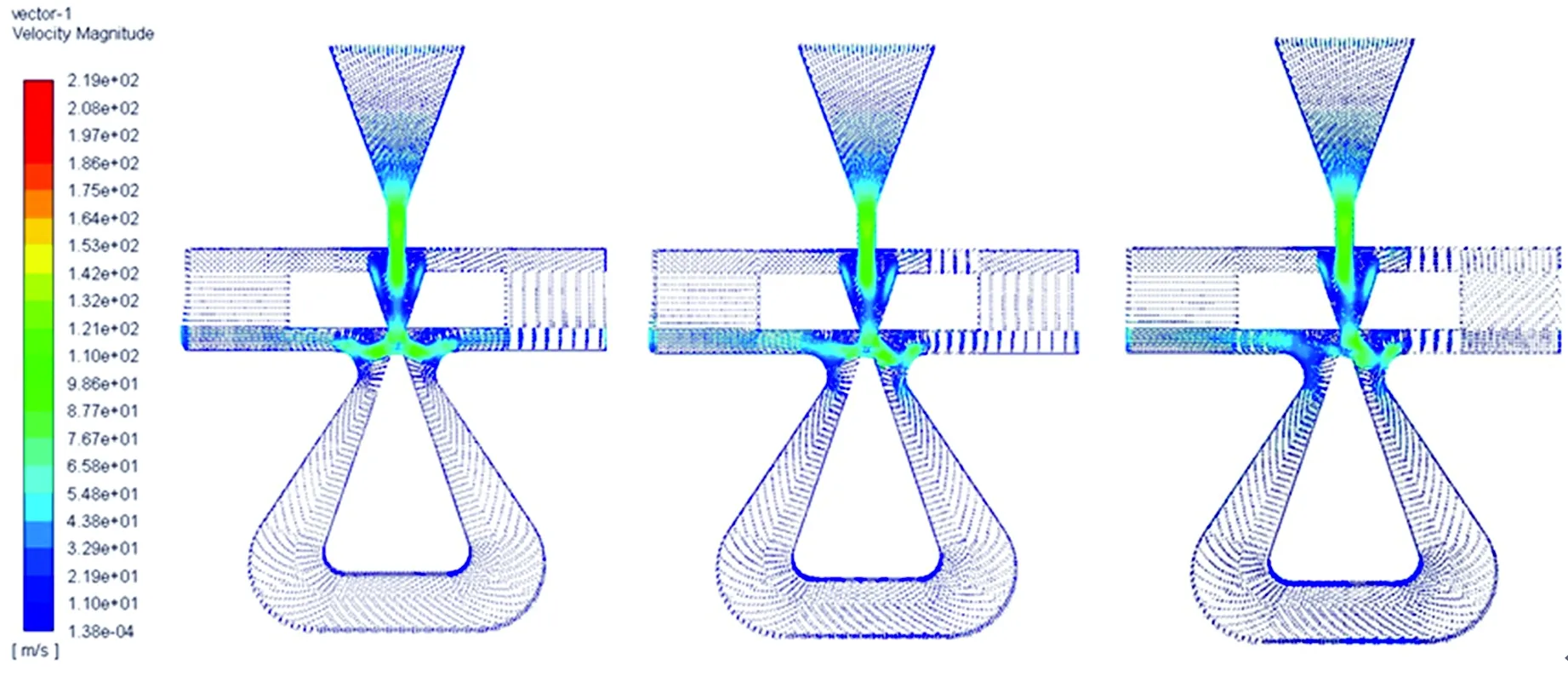
(a)无偏移 (b)偏移0.02 mm (c)偏移0.04 mm
图7 偏转板向右偏移时前置级流量模型的速度矢量图
Fig.7 Velocity vector diagrams of pre-stage flow model when the deflector moves to the right
3.2 前置级结构参数对静态特性的影响
3.2.1 劈尖高度变化
劈尖高度变化示意图如图8所示,其中劈尖宽度和左右接收孔内外侧夹角均保持不变。为保持夹角不变,图8(a)和图8(b)中左右接收孔道内壁分别平行向内侧靠近、平行向外侧移动。
在不同劈尖高度下前置级的静态特性曲线如图9所示。从图9(a)中可以看出,右接收孔的压力随着偏转板向右移动而逐渐增大,劈尖高度减小0.05 mm时,右接收孔的压力最大,这是由于此时劈尖形状是最小的,劈尖对喷射油的损耗最低。从图9(b)中可以看出,左右接收孔的压力差随着偏转板向右移动而逐渐增大,三种不同劈尖高度下左右接收孔的压差曲线基本成线性。从图9(c)中可以看出,劈尖高度减小0.05 mm时,前置级流量最大,这是由于劈尖高度降低,更多的流量进入到降低的凹槽中,使流量增大。
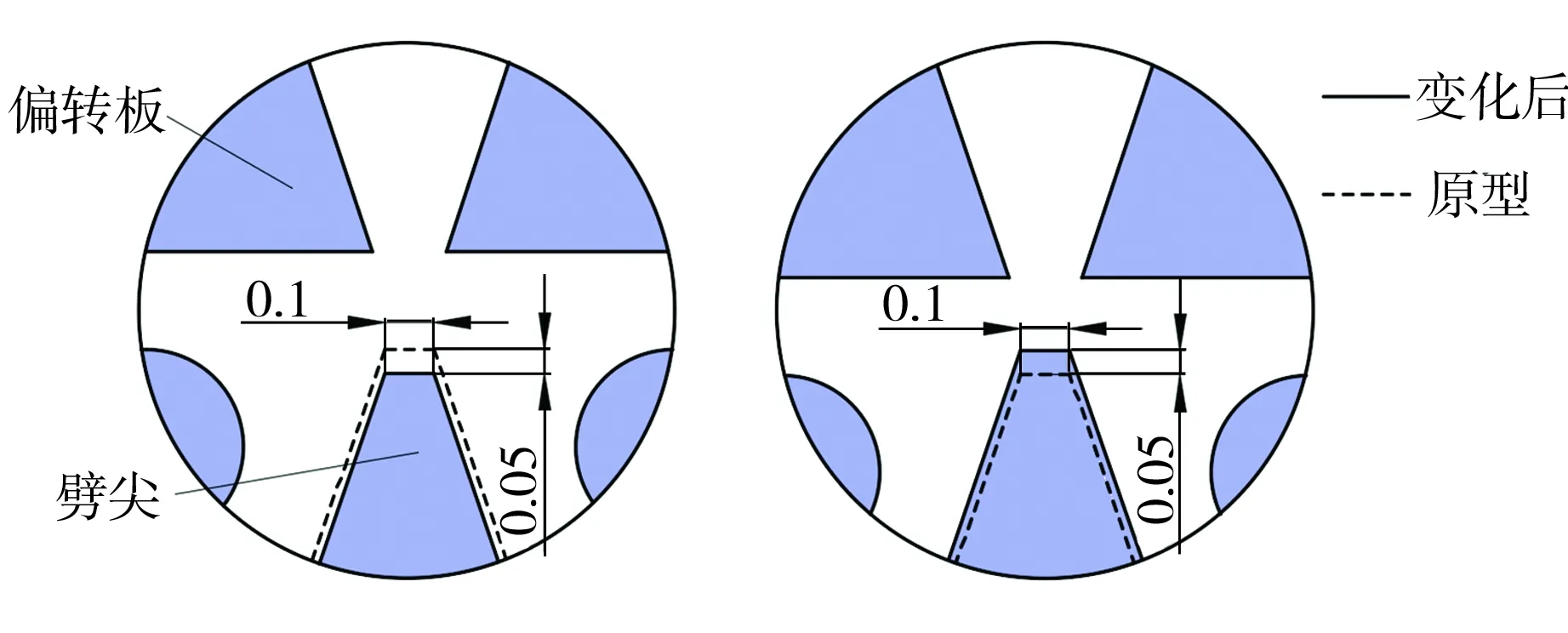
(a)高减小 (b)高增加
图8 劈尖高度变化示意图
Fig.8 Schematic diagrams of wedge height change
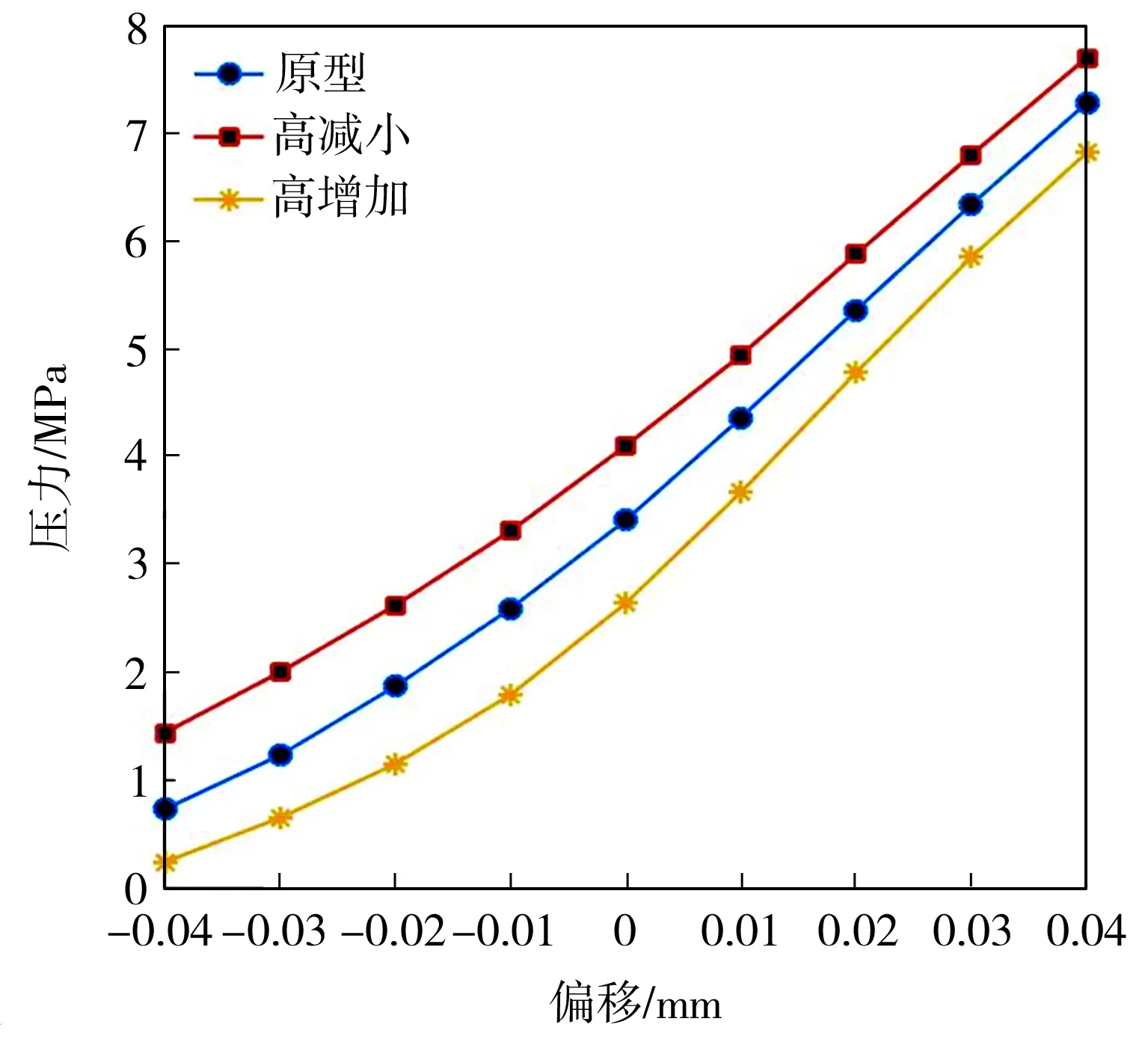
(a)右接收孔的压力曲线
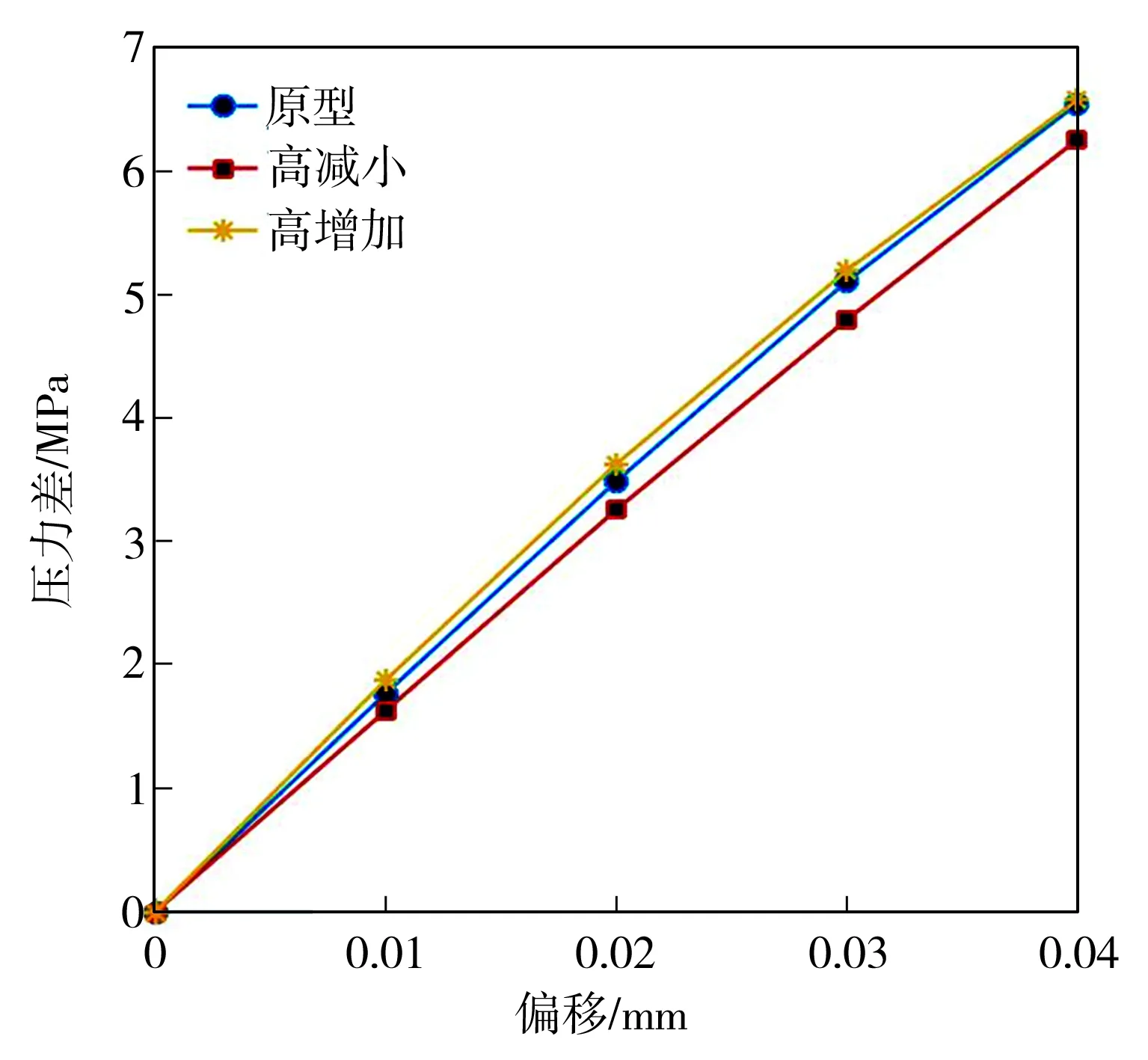
(b)左右接收孔的压差曲线

(c)流量曲线
图9 在不同劈尖高度下前置级的静态特性曲线
Fig.9 Static characteristic curves of pre-stage at different wedge heights
3.2.2 劈尖高度和宽度同时变化
劈尖高度和宽度变化示意图如图10所示。图10中左右接收孔内外侧夹角均保持不变,图10(a)表示劈尖高度减小0.05 mm,劈尖宽度随之变大;图10(b)表示劈尖高度增加0.05 mm,劈尖宽度随之变小。
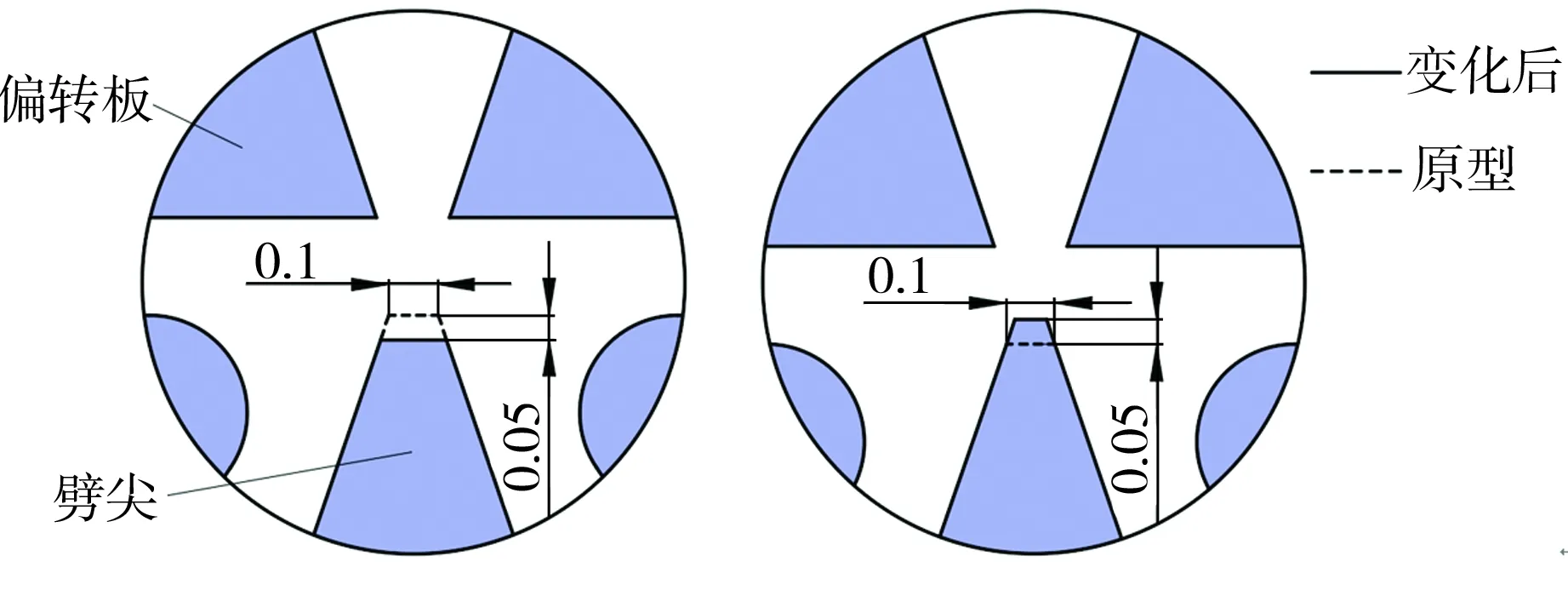
(a)高减小,宽变大 (b)高增加,宽变小
图10 劈尖高度和劈尖宽度变化示意图
Fig.10 Schematic diagrams of wedge height and width change
在不同劈尖高度和宽度下前置级的静态特性曲线如图11所示。从图11(a)中可以看出,在偏转板向左位移0.04 mm时,三者在右接收孔的压力基本相同,劈尖高度增加0.05 mm,且宽度变小时,右接收孔的压力曲线线性度最好,压力最大。从图11(b)中可以看出,三者压差曲线基本成线性,劈尖高度减小0.05 mm,且宽度变大时,左右接收孔的压差曲线线性度最好,但压力增益最低。从图11(c)中可以看出,劈尖高度增加0.05 mm、宽度变小时,前置级的流量曲线线性度最差,其流量最大,这是由于劈尖宽度最小,导致流量提前分流,喷射流损耗少,使流量增大。
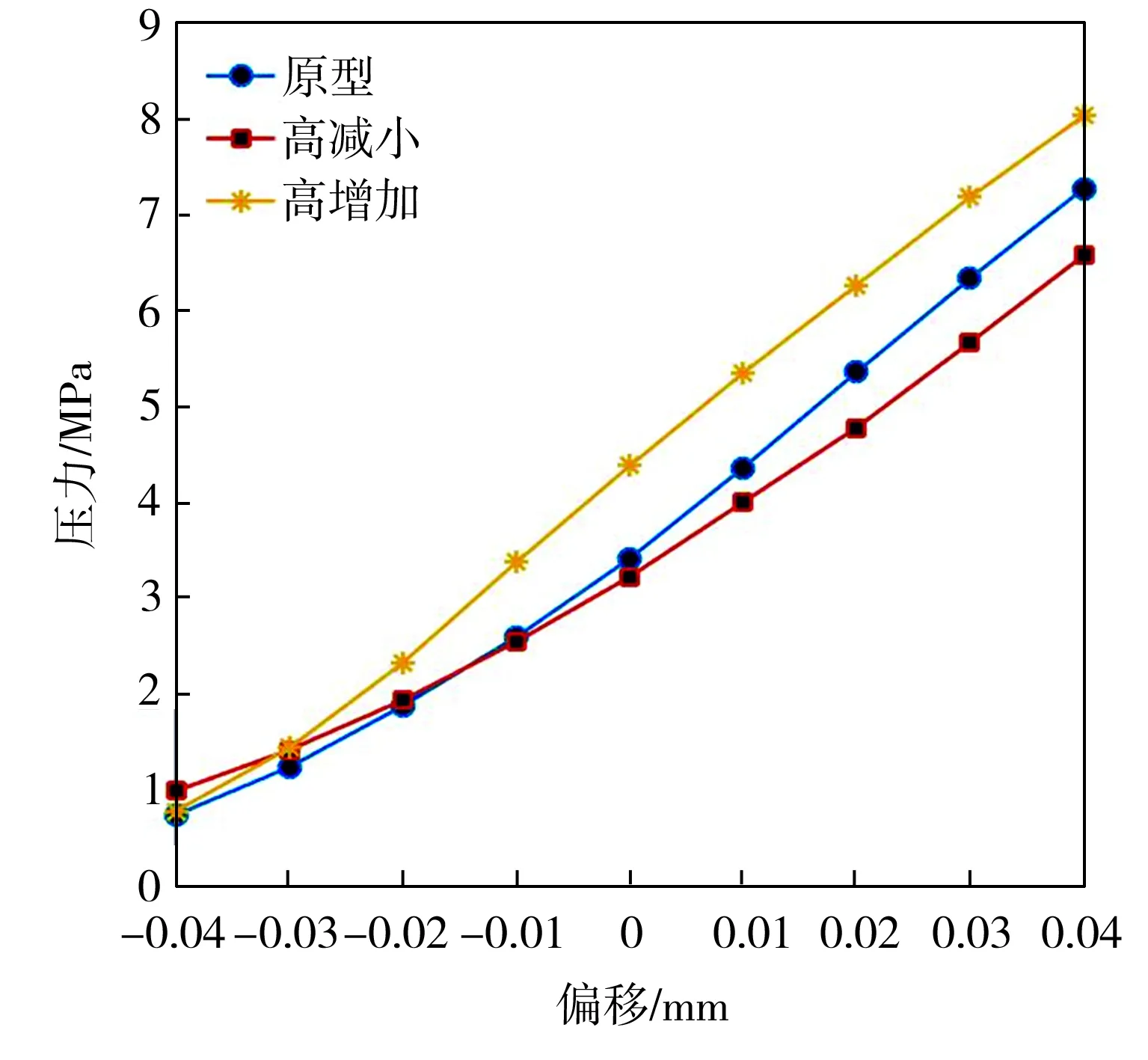
(a)右接收孔的压力曲线
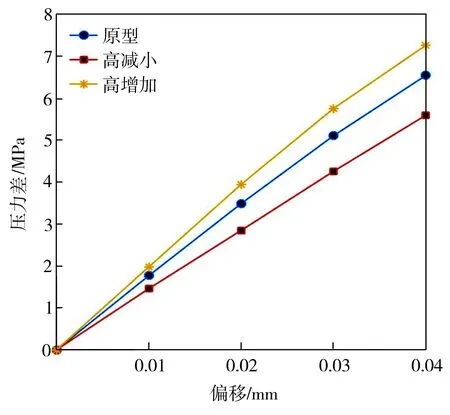
(b)左右接收孔的压差曲线
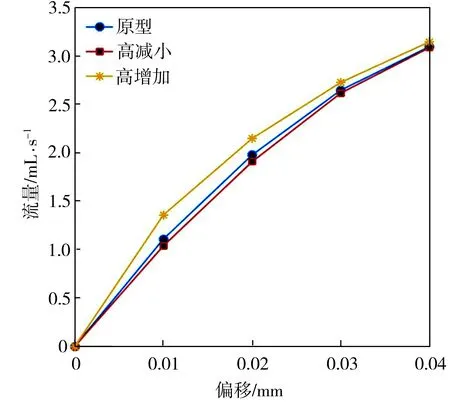
(c)流量曲线
图11 在不同劈尖高度和宽度下前置级的静态特性曲线
Fig.11 Static characteristic curves of pre-stage at different wedge heights and widths
3.2.3 V形槽喷口导流长度加长
在V形槽喷口宽度不变时,增加喷口导流长度示意图如图12所示。图12(a)表示V形槽喷口导流长度增加0.05 mm,偏转板下端喷口与接收孔的距离(d)变小至0.15 mm;图12(b)表示V形槽喷口导流长度增加0.05 mm,偏转板下端喷口与接收孔距离(d)保持不变。
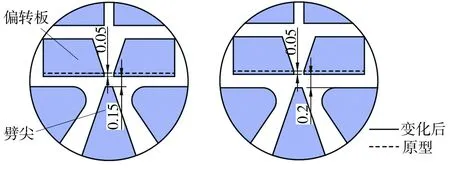
(a)导流加长,d变小 (b)导流加长,d不变
图12 增加V形槽喷口导流长度示意图
Fig.12 Schematic diagrams of increasing guide length of nozzle of v-groove
在不同V形槽喷口导流长度下前置级的静态特性曲线如图13所示。从图13(a)中可以看出,导流加长0.05 mm、偏转板下端喷口与接收孔的距离(d)变小时,右接收孔的压力最大,这是由于V形槽喷口端部增加导流作用,更多的油液进入接收孔。从图13(b)中可以看出,原型前置级的压差曲线线性度最好,压力增益最大。从图13(c)中可以看出,导流加长0.05 mm、偏转板下端喷口与接收孔的距离(d)变小时,前置级的流量曲线线性度最好,但流量增益最小。
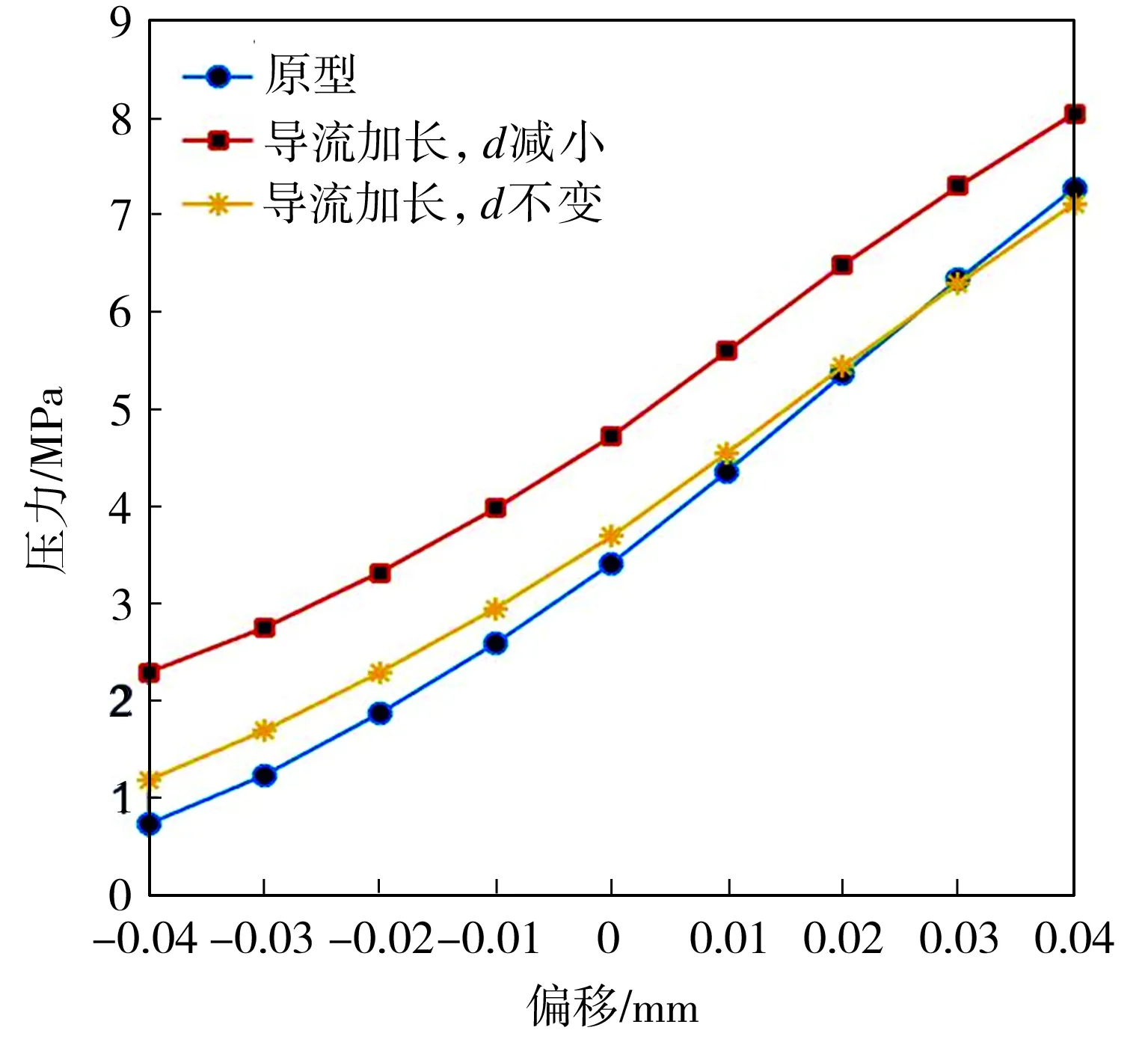
(a)右接收孔的压力曲线
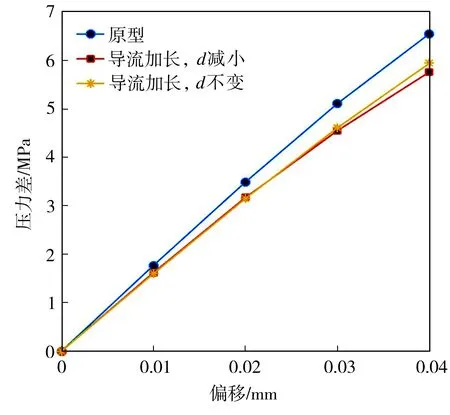
(b)左右接收孔的压差曲线
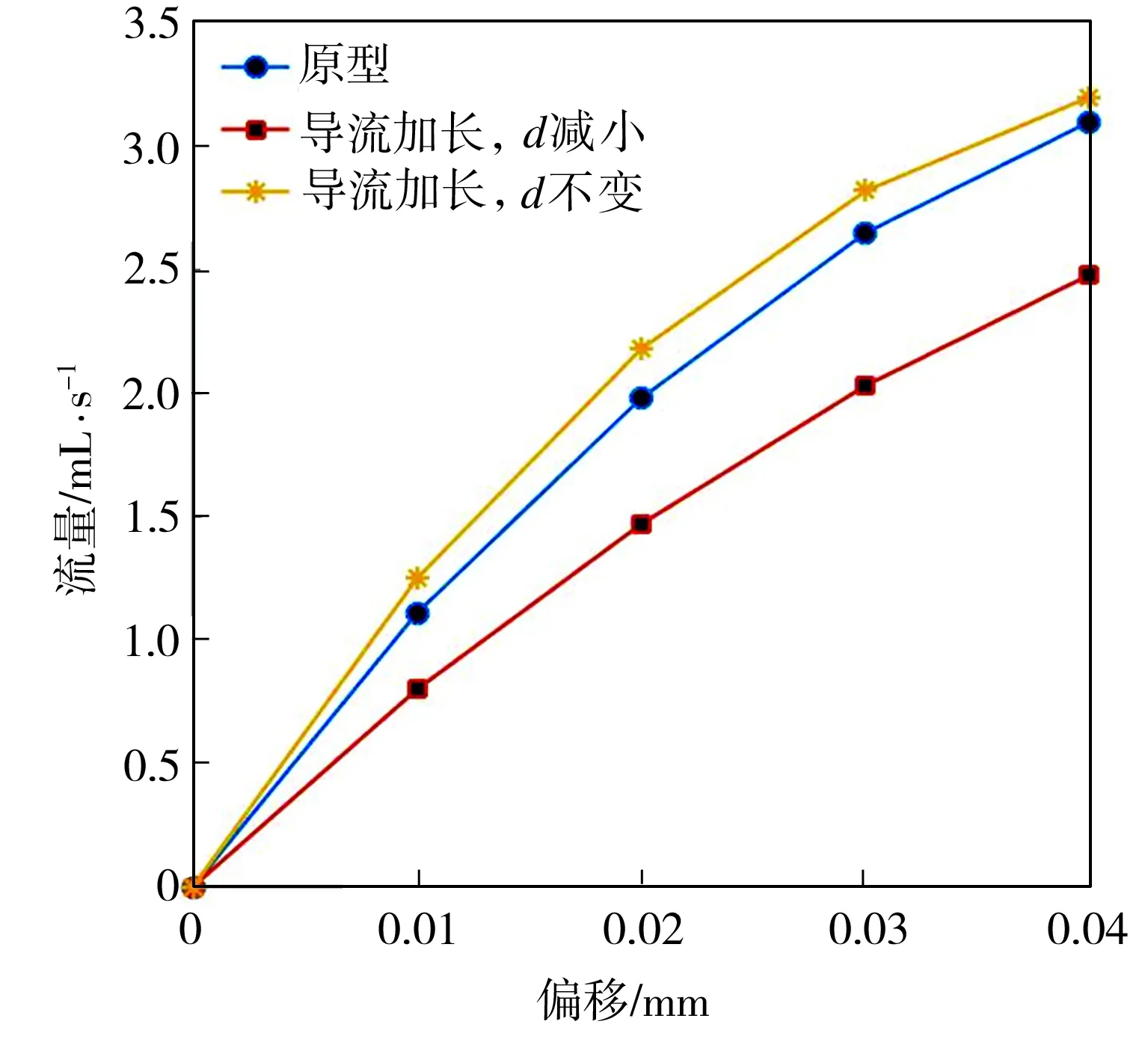
(c)流量曲线
图13 在不同V形槽喷口导流长度下前置级的静态特性曲线
Fig.13 Static characteristic curves of pre-stage at different guide lengths of nozzle of v-groove
4 偏转板伺服阀系统动态特性分析
4.1 系统数学模型的建立
对前置级的流量曲线进行二次拟合,从而得到不同前置级结构的流量(y)与偏转板位移(x)的关系式为:
(a)原型
ya=-1100x2+120x+0.0029
(1)
(b)劈尖高减小0.05 mm,劈尖宽不变
yb=-2000x2+170x+0.002
(2)
(c)劈尖高增加0.05 mm,劈尖宽变小
yc=-1500x2+140x+0.045
(3)
(d)喷口导流加长0.05 mm,偏转板下端喷口与接收孔的距离(d)变小
yd=-580x2+85x+0.0023
(4)
根据式(1)~(4)可得到四条流量曲线的流量增益分别为:
Kqra=0.12 m3/(s·m)
(5)
Kqrb=0.17 m3/(s·m)
(6)
Kqrc=0.14 m3/(s·m)
(7)
Kqrd=0.085 m3/(s·m)
(8)
力矩马达输出简化模型为:
Td=Kmθ+KtΔi
(9)
式中,Td为力矩马达输出力矩,N·m;Km为磁弹簧的刚度,N·m/rad;θ为衔铁偏转的角度,rad;Kt为力矩系数,N·m/A;Δi为线圈之间的信号电流差,A。
衔铁组件的平衡模型为:
(10)
式中,ic为线圈之间的信号电流,A;Ja为衔铁转动惯量,kg·m2;Ba为衔铁阻尼系数,N/(m·s-1);Kmf为力矩马达综合刚度,N·m/rad;Kf为反馈杆的刚度,N/m;r为反馈杆下端小球的球心到偏转中心的距离,m;xv为滑阀阀芯的位移,m。
偏转板偏移模型为:
xj=bsinθ≈bθ
(11)
式中,xj为偏转板位移量,m;b为偏转板中心到旋转中心的距离,m。
前置级的流量模型为:
QL=Kqrxj-KcrPL
(12)
式中,QL为前置级的输出流量,m3/s;Kqr为前置级的流量增益,m3/(s·m);Kcr为流压系数,m3/(s·Pa)-1;PL为阀芯两端的压差,Pa。
主阀的流量模型为:
(13)
式中,Av为主阀芯的端部面积,m2。
主阀芯的力平衡模型为:
Kfxv+Kfrθ+0.43wPsxv
(14)
式中,Mv为主阀芯的质量,kg;Bv为主阀芯的运动系数,N·s/m;Ps为液压油进口压力,Pa;w为阀芯过流面积的梯度,m。
对式(10)~(14)分别进行拉普拉斯变换得到如下模型:
KtIc=Jas2θ+Basθ+Kmfθ+KfrXv
(15)
Xj=bθ
(16)
QL=KqrXj-KcrPL
(17)
QL=AvsXv
(18)
PLAv=Mvs2Xv+BvsXv+KfXv+
Kfrθ+0.43wPsXv
(19)
4.2 仿真分析
由于滑阀在运动过程中产生的黏性阻尼力、反馈杆对滑阀的反作用力和稳态液动力比其惯性力和两端产生的压差力小得多,因此将它们忽略以简化计算,综合考虑式(15)~(19)之间的关系,可绘制如图14所示的偏转板伺服阀系统方框图。偏转板伺服阀的各动态仿真参数如表1所示。
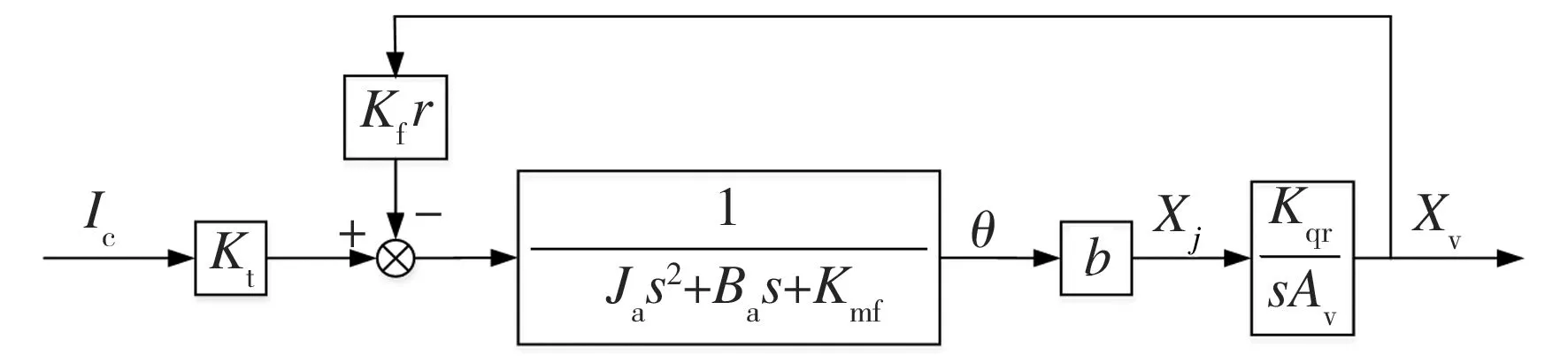
图14 偏转板伺服阀系统简化方框图
Fig.14 Simplified block diagram of deflector servo valve system

表1 偏转板伺服阀的主要仿真参数
根据偏转板伺服阀系统方框图,调用仿真模块,可搭建SIMULINK系统模型。将表1中的数值输入到相应模块中进行仿真分析,可得到如图15所示的偏转板伺服阀系统四种模型的伯德图。从图15中可以看出,原型系统的幅频宽和相频宽分别为60.27、101.70 Hz;当劈尖高度减小0.05 mm、劈尖宽度不变时,系统幅频宽和相频宽分别为109.80、121.00 Hz;当劈尖高度增加0.05 mm、劈尖宽度变小时,系统幅频宽和相频宽分别为76.28、109.80 Hz;当V形槽下端喷口导流长度增加0.05 mm、偏转板下端喷口与左右接收孔的距离(d)变小时,系统幅频宽和相频宽分别为38.30、85.61 Hz。由此可见,与原型相比较,无论是增加劈尖高度还是减小劈尖高度,都可增加偏转板伺服阀的响应频率,提升其动态性能;而劈尖高度减小0.05 mm,偏转板伺服阀的动态性能提升更为显著;增加导流长度,偏转板下端喷口与接收孔的距离(d)变小时,反而降低了偏转板伺服阀的动态响应性能。
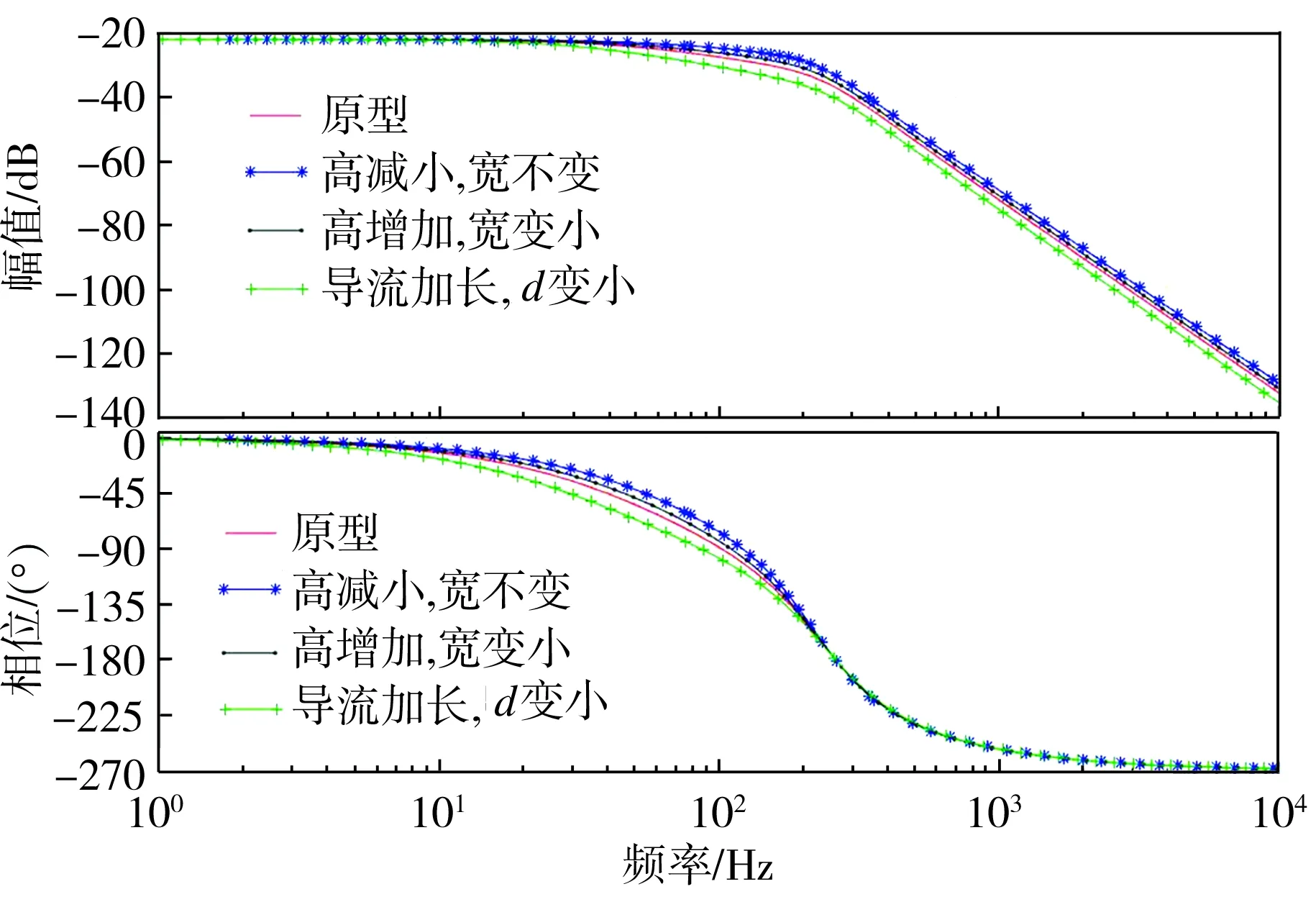
图15 偏转板伺服阀系统四种模型的伯德图
Fig.15 Bode diagrams of four system model of deflector servo valve
5 结论
(1)通过对偏转板伺服阀前置级流场的静态特性和偏转板伺服阀系统动态特性分析得到,适当降低劈尖高度,有利于增大前置级的流量增益,同时提高偏转板伺服阀的响应频率,提升其动态性能。
(2)当劈尖高度增加、宽度变小时,可以增大前置级的压力增益和流量增益,但其流量曲线线性度较差。
(3)当V形导流槽喷口导流长度加长、偏转板下端喷口与接收孔距离减小时,可以提高前置级流量曲线的线性度,但会减小前置级流量增益,降低伺服阀的响应频率。
