颗粒脱黏对异质摩擦界面点接触弹流润滑的影响
2019-10-11柴宇峰曾良才陈克应
柴宇峰,曾良才,陈克应
(1.武汉科技大学机械自动化学院,湖北 武汉,430081;2. 武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081)
弹流润滑接触对接触组件的表面形貌非常敏感,后者不仅影响润滑油膜的形状和压力分布,还会造成接触区域的油膜发生干接触从而导致混合润滑的产生。异质材料中的颗粒对接触区域应力分布及表面位移有重要影响,当应力足够大时,材料表层会因颗粒的存在而呈现出匀质材料所没有的特殊形貌[1-3]。文献[4]通过优化颗粒的空间分布参数(埋布深度、颗粒间距、排列方式)和尺寸参数,减小了颗粒增强型复合材料中基体与颗粒间的摩擦力。目前,金属基复合材料的制备工艺复杂、成本昂贵,并且在制备过程中其基体与颗粒间易产生残余应力,造成二者接触界面脱黏[5-8]。再则,当复合材料受到重载时,应力会完成从基体界面到颗粒界面之间的传递,因此界面行为将成为复合材料失效的主要原因[9]。此外,颗粒和基体界面的脱黏势必影响接触区域的表面形貌,进而改变弹流润滑特性。故本文通过建立单个颗粒在接触区域与基体脱黏的半空间点接触模型,运用弹性流体动压润滑方程进行数学建模,分析了不同脱黏形式对接触区域油膜厚度和压力分布的影响,并且对异质材料的最大剪应力进行了研究,以期为实际工程中重载下的弹流润滑问题提供理论支持。
1 模型与仿真
1.1 模型的建立
1.1.1 几何模型
接触半球与接触平面之间的点接触弹流润滑模型及颗粒上方脱黏示意图分别见图1及图2。其中图1所示模型基于如下假设:(1)接触半球与接触平面之间不存在滚动,即覆于半球表面的油液速度与半球运动速度相同,接触类型为纯滑动;(2)液压油为牛顿流体;(3)因接触平面曲率半径极大,故忽略油膜曲率的影响;(4)不考虑油温的变化,即该模型为等温点接触弹流润滑模型;(5)忽略接触面间的粗糙度。图1中半球与平面沿x方向的速度分别为u1、u2,由于接触平面静止,故u2为0。图2中l为颗粒的脱黏距离,d为颗粒的埋布深度,L为立方颗粒的边长。
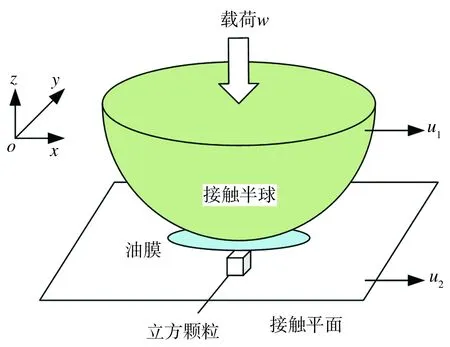
图1 接触半球与接触平面的点接触弹流润滑模型
Fig.1 Point contact elastohydrodynamic lubrication model of contact hemisphere and contact plane

图2 颗粒上方脱黏示意图
Fig.2 Schematic diagram of debonding above the particles
1.1.2 无量纲化处理
1.1.3 负载平衡方程
半球平面在负载作用下,油膜压力p和负载压力w的平衡方程为
(1)
式中:xi、yi分别为x、y方向上边界内的积分变量;xi-in、yi-in及xi-out、yi-out分别为x、y方向的进口及出口边界值。
1.1.4 膜厚方程
夹杂物弹流润滑的接触变形可以分为两部分,即夹杂颗粒引起的接触表面的弹性变形和点接触时弹流润滑的弹性变形[10]。对于本研究模型,需考虑颗粒及脱黏区域引起的弹性变形,为了便于求解,借助ANSYS软件分别建立干接触下无颗粒点接触模型及含有脱黏区域的单颗粒点接触模型,这两个模型在接触表面产生的弹性变形量的差值即为含脱黏区域模型中颗粒所引起的弹性变形量。含脱黏区域模型中颗粒引起的弹性变形会引起接触表面位移的变化,记该位移为s(xi,yi),则油膜厚度方程为
s(xi,yi)
(2)
式中:h(xi,yi)为实际油膜厚度;h0为接触区域的刚体位移;x′i、y′i分别为xi及yi的导数;Ω表示接触区域;方程式右侧第三项表示无颗粒点接触弹流润滑的弹性变形。该方程的无量纲形式为
+S(X,Y)
(3)
式中:X、Y及X′、Y′分别为xi、yi及x′i、y′i的无量纲形式;Xin、Yin及Xout、Yout分别为xi-in、yi-in及xi-out、yi-out的无量纲形式;S(X,Y)=s(xi,yi)/L。
1.1.5 黏压方程
在不考虑温度影响下,点接触弹流润滑方程[11]为
η=η0exp{(lnη0+9.67)[(1+
5.1×10-9p(x,y))n-1]}
(4)
式中:η为实际油液黏度,n与黏压系数α的关系为:n=α/[5.1×10-9(lnη0+9.67)]。
1.1.6 控制方程
基于模型做出的假设,点接触弹流润滑的Reynold方程[12]为
(5)
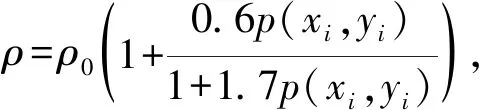
(6)
1.1.7 边界条件
用Reynold方程的边界条件来限定接触区域的进口压力和出口压力,无量纲形式为
(7)
1.1.8 迭代求解
采用有限差分多重网格法对压力进行求解,将接触面离散化[13]。因为脱黏颗粒引起的表面位移可由ANSYS软件仿真获得,所以只需要将该部分位移S(X,Y)与点接触弹流润滑的形变进行耦合,然后判断其是否收敛。具体耦合算法的流程图如图3所示。
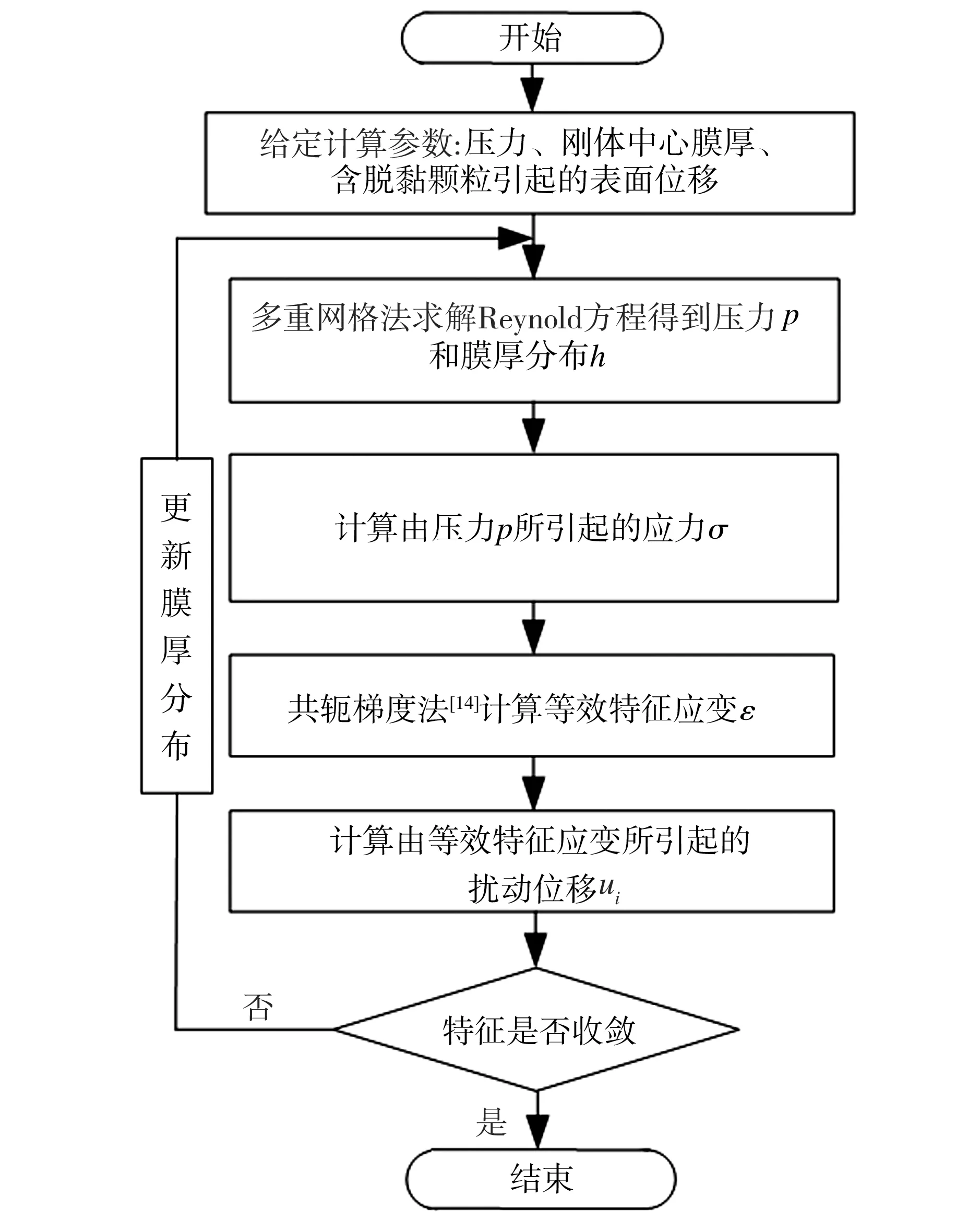
图3 迭代流程图
1.2 仿真实验
利用MATLAB对接触区域的流场进行仿真,通过耦合算法得到模型xoz平面的油膜压力分布和油膜厚度。计算域边界:Xin=-2,Xout=1.5;颗粒分布区间:X∈[-0.5,-0.3]。仿真参数如表1所示。

表1 仿真参数
2 分析与讨论
2.1 脱黏距离对油膜厚度的影响
当颗粒埋布深度d为0.2 mm,弹性模量E3为450 GPa时,在不同脱黏距离条件下,油膜的厚度变化如图4所示。由图4可见,无论脱黏位置处于颗粒上方还是下方,在不同脱黏距离条件下,颗粒分布区间附近的等效油膜厚度均大于该区间含颗粒未脱黏或不含颗粒条件下的相应值,而在远离颗粒分布区间处,上述各组油膜厚度并无明显差别。这是因为油膜的压力可以平衡外部载荷, 在相同的外力作用下,颗粒相对于周围基体的变形量能够使颗粒有效地承受或分散其所在区域的压力,故颗粒分布区域的油膜厚度变化趋势与无颗粒分布区域不同。值得注意的是,当脱黏位置处于颗粒上方时,油膜厚度在颗粒分布区域附近沿X方向先增大后减小,其变化曲线出现明显的波峰,且峰值随着脱黏距离的增大而增高,这将使颗粒接触区域积累更多的润滑液,而当油液移出颗粒接触区域后,油膜厚度迅速减小,形成较为明显的颈缩。此外,因颗粒可以承受来自基体的压力,使得接触面位移减小,故在颗粒分布区域附近未发生颗粒脱黏时的油膜厚度低于不含颗粒条件下的相应值,不过此处一旦发生颗粒脱黏,接触面的位移将迅速增大,从而导致油膜厚度突然增加并超过后者。当脱黏位置处于颗粒下方时,颗粒分布区域附近的油膜厚度受脱黏距离影响较小且沿X方向无明显改变,这是因为颗粒此时仍然能够承受基体施加的压力,不会在接触面形成较大的位移。
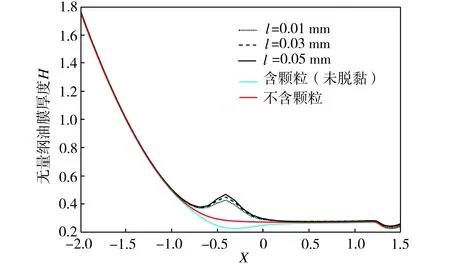
(a)颗粒上方脱黏
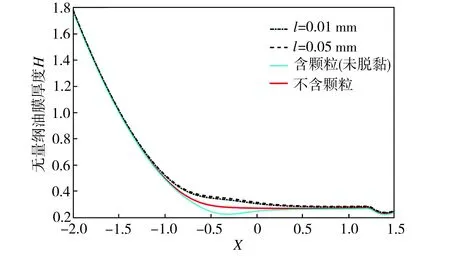
(b)颗粒下方脱黏
Fig.4 Oil film thickness at different debonding distances
2.2 不同埋布深度的颗粒脱黏对油膜厚度的影响
当颗粒上方脱黏距离l为0.05 mm,弹性模量E3为450 GPa时,在不同颗粒埋布深度条件下,油膜的厚度变化如图5所示。由图5可见,颗粒分布区间附近的油膜厚度随着埋布深度的增加而减小,但均高于不含颗粒条件下的相应值。此外,当颗粒埋布深度小于0.4 mm时,颗粒分布区域附近油膜厚度沿X方向的变化曲线出现明显波峰,而当埋布深度继续增大时,油膜厚度在此区间无明显改变,表明此时脱黏颗粒对于接触面位移的影响较小,因此当颗粒埋布深度超过1.0 mm时,基本可以忽略颗粒脱黏对弹流润滑膜厚的影响。
2.3 不同弹性模量的颗粒脱黏对油膜厚度的影响
当颗粒上方脱黏距离l为0.05 mm,埋布深度d为0.2 mm时,在不同弹性模量的颗粒脱黏条件下,油膜的厚度变化如图6所示。由图6可见,在颗粒分布区间附近,不同颗粒弹性模量条件下的油膜厚度变化曲线均沿X方向出现明显的波峰,且油膜厚度随着弹性模量的增加而增大。此外,值得指出的是,当颗粒弹性模量不低于450 GPa时,油膜厚度变化曲线波峰更加尖锐,且随着弹性模量继续增加,油膜厚度增幅极小,这是因为此时由颗粒弹性模量变化所引起的接触表面位移变化相比由颗粒脱黏所引起相应变化已经微不足道;当颗粒弹性模量较低时,颗粒分布区域附近的油膜厚度相比高弹性模量条件下的相应值降幅明显,油膜厚度变化曲线的波峰也逐渐平缓,这是因为弹性模量较小的颗粒可以分散其所在区域的压力,一旦发生颗粒脱黏,就会造成应力无法完全分散到周围基体,从而导致接触表面产生较大位移,故在颗粒弹性模量较小的条件下,油膜厚度对颗粒弹性模量的变化更为敏感。
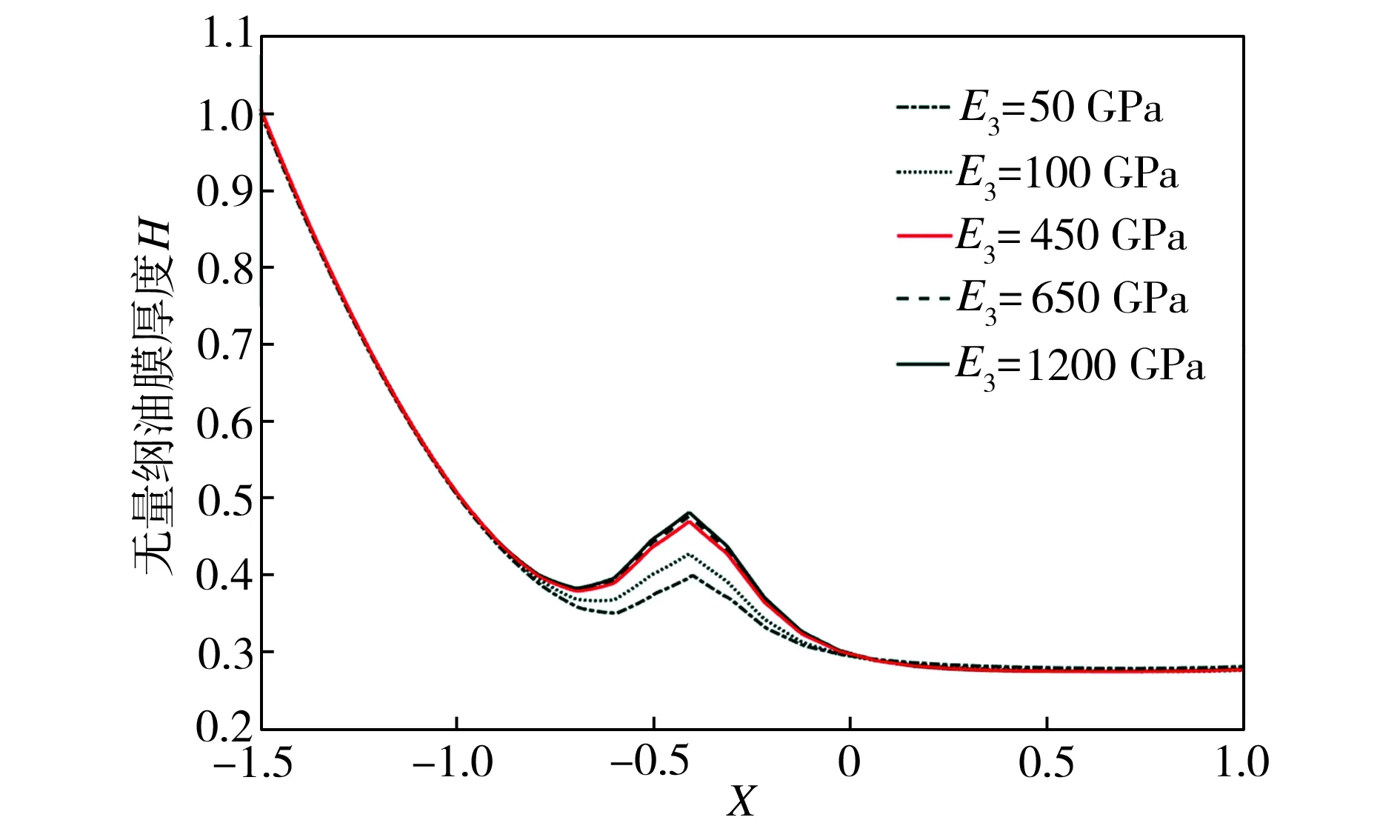
图6 不同弹性模量时的油膜厚度
2.4 颗粒脱黏对油膜压力的影响
当颗粒上方脱黏距离l为0.05 mm,埋布深度d为0.2 mm,颗粒弹性模量E3为450 GPa,颗粒脱黏或未脱黏时的油膜压力分布如图7所示。从图7中可见,相比无颗粒状态,当接触面颗粒未脱黏时,颗粒分布区域内的油膜压力明显激增,相应压力分布曲线出现波峰,这是因为在颗粒分布区的接触面上存在微凸体,使油膜厚度减小,造成油膜在进入颗粒分布区时形成颈缩;当接触面颗粒脱黏时,该界面将在此处产生较大位移,造成油膜厚度增加,油膜压力相对较低,而当油膜移出颗粒分布区域时,由于油膜厚度急剧减小,会立即形成颈缩,造成压力激增,此时最大压力值约为匀质接触面相应值的3倍,这对于弹流润滑非常不利。

图7 颗粒脱黏对油膜压力的影响
2.5 颗粒脱黏对异质材料内部最大剪应力的影响
泊松比v3为0.30、弹性模量E3为450 GPa的颗粒未脱黏或上方脱黏(脱黏距离l为0.05 mm)、埋布深度d为0.2 mm时,相应异质材料内部的剪应力分布如图8所示。由图8可见,与颗粒未脱黏时相比,颗粒脱黏造成材料基体与颗粒间出现间隙,使得颗粒周边应力集中严重,最大剪应力甚至达到颗粒未脱黏时相应值的25倍以上,这将导致异质材料出现裂纹,甚至发生断裂。
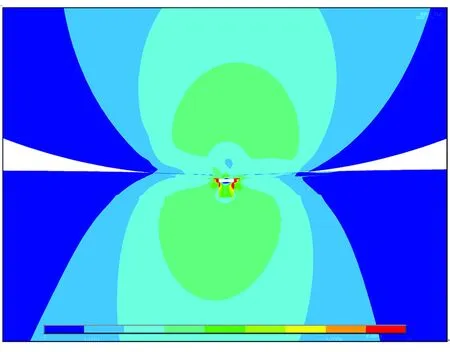
(a)颗粒上方脱黏
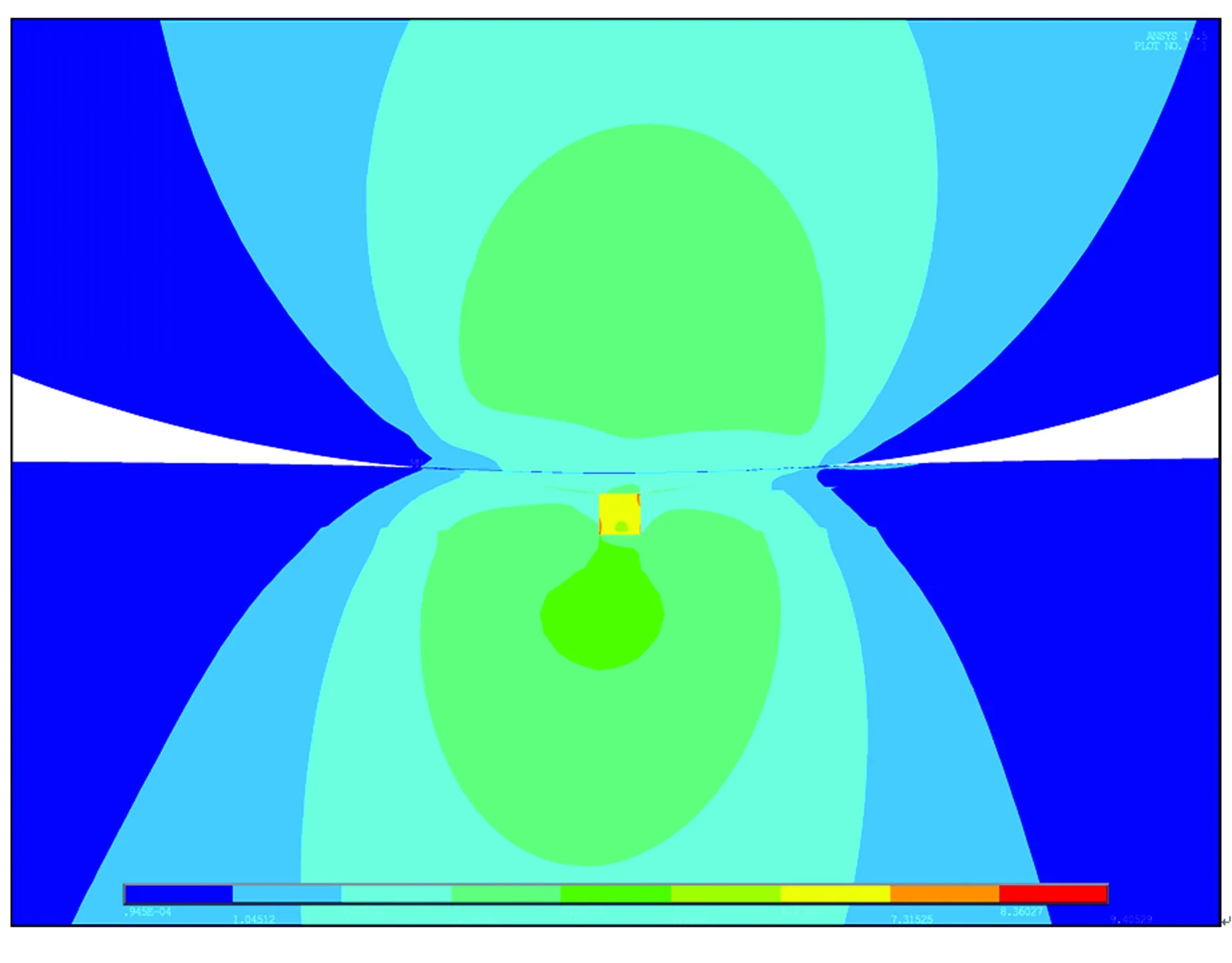
(b)颗粒未脱黏
弹性模量E3分别为450 GPa及100 GPa、泊松比v3分别为0.30及0.21的颗粒脱黏时,相应材料的最大剪应力随脱黏距离的变化如图9所示。由图9可以看出,颗粒脱黏均造成异质材料内部最大剪应力相比颗粒未脱黏时显著增加,其中高弹性模量颗粒脱黏造成的材料最大剪应力增幅更大,这是因为低弹性模量颗粒更易将所受应力分散到基体中,所以对材料最大剪应力的提升作用不如前者明显。此外,当脱黏颗粒弹性模量较高时,异质材料内部的剪切应力随着脱黏距离的增大而减小,这是因为高弹性模量颗粒所受基体压力较大,脱黏距离越小,越易在颗粒边缘形成尖端从而导致应力集中。而弹性模量较低的颗粒变形量大,当其脱黏距离较小时,部分颗粒依然与基体接触,因此颗粒所受应力仍能分散到基体中,不过随着脱黏距离的增大,颗粒逐渐脱离与基体的接触从而造成应力集中加剧,故相应异质材料的最大剪应力随脱黏距离的增加而不断增大。
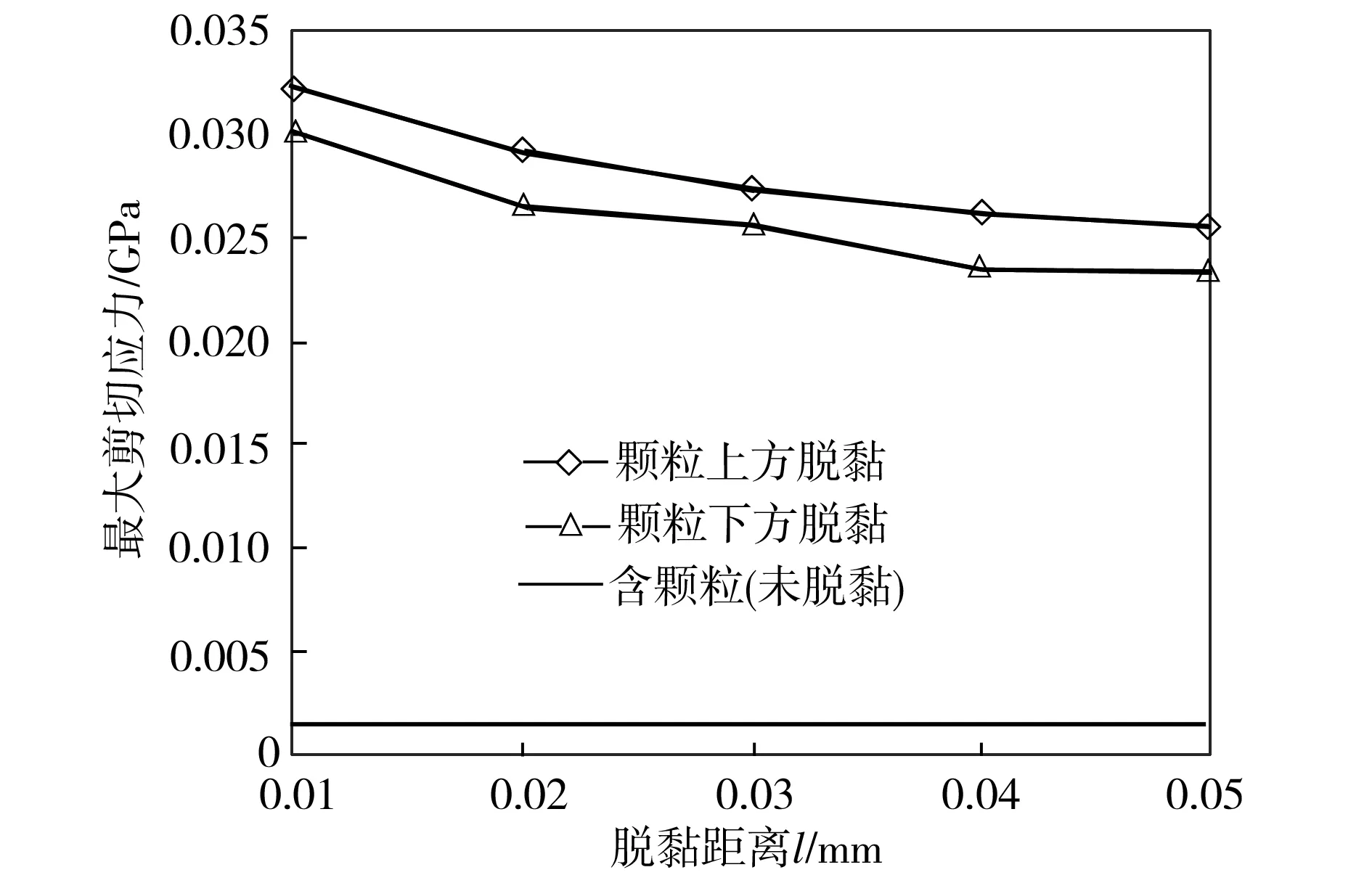
(a)弹性模量450 GPa
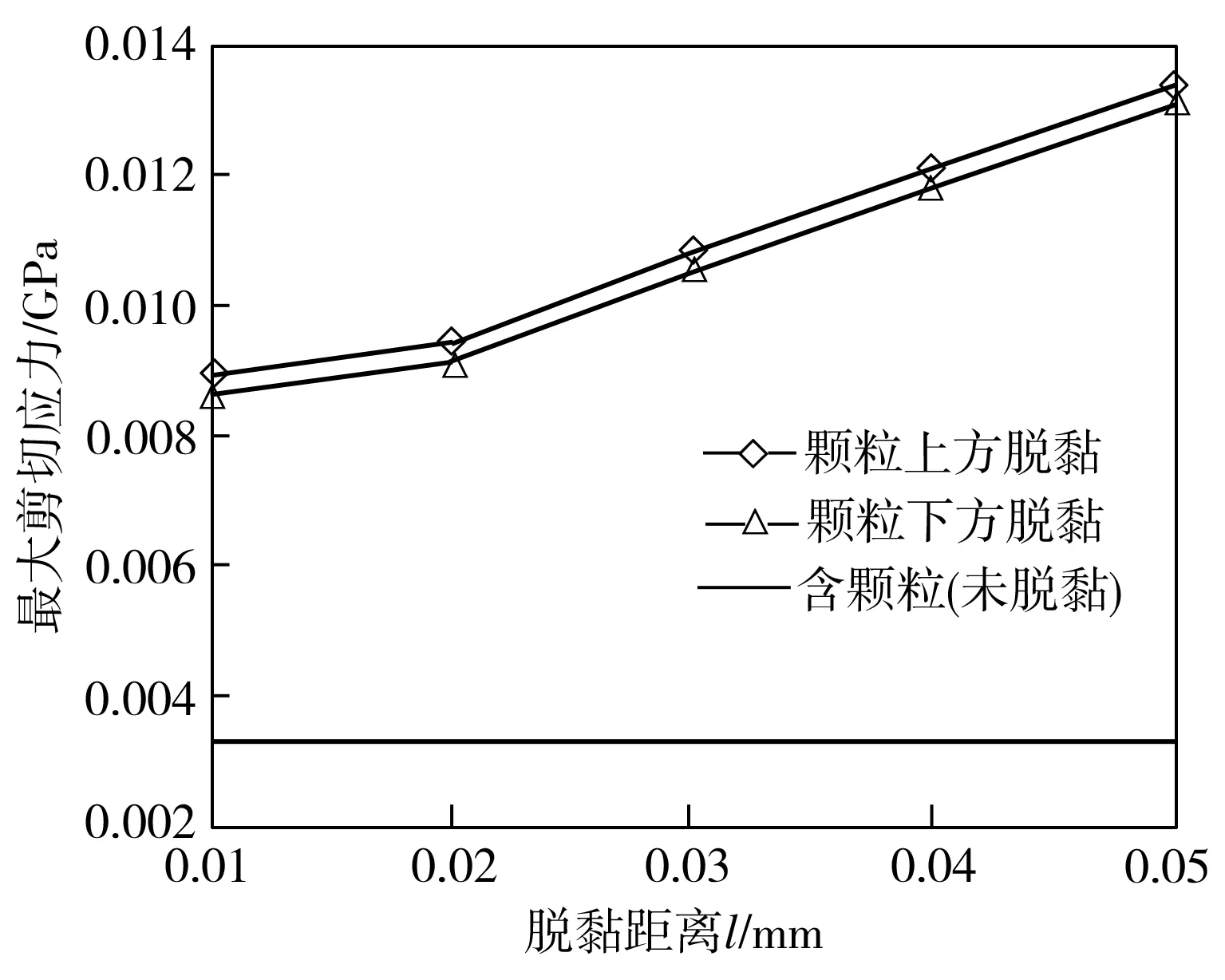
(b)弹性模量100 GPa
Fig.9 Internal maximum shear stress at different debonding distances
3 结论
(1)当颗粒上方脱黏时,颗粒分布区域附近的油膜厚度随颗粒脱黏距离及弹性模量的增加而增大,随颗粒埋布深度的增加而减小,当颗粒埋布深度超过1.0 mm时,基本可以忽略其脱黏对弹流润滑膜厚的影响。当颗粒下方脱黏时,颗粒分布区域附近的油膜厚度受脱黏距离影响较小。
(2)在颗粒上方脱黏条件下,当油液移出颗粒分布区域时,因油膜厚度迅速减小将会导致油膜压力激增。
(3)颗粒脱黏造成异质材料内部最大剪应力相比颗粒未脱黏时显著增加,当脱黏颗粒弹性模量较高时,该增幅尤其明显,且剪应力随脱黏距离的增加而减小;当脱黏颗粒弹性模量较低时,该剪应力随脱黏距离的增加而增大。
