平整轧制多变量系统的线性自抗扰解耦控制

李鹏威，王 京

(1. 北京科技大学工程技术研究院，北京，100083；2. 北华大学电气与信息工程学院，吉林 吉林，132013)

板带钢平整轧制过程中，板形和板厚作为相互影响又紧密联系的两个重要指标，其精度直接关系到冷轧带钢成品板质量的优劣[1-3]。然而，平整机板形板厚多变量控制系统中两者之间存在强耦合关系，并且系统也受到了随机扰动和对象模型参数时变等因素的影响，这就要求系统控制器在设计上需同时满足解耦控制和鲁棒性两点。近年来，随着自抗扰控制技术(active disturbance rejection control，ADRC)的不断发展[4-5]，国内外研究者针对此类多变量耦合系统已开展了大量的研究工作，如文献[6]利用扩张状态观测器(ESO)对系统中耦合项和不确定项进行观测，同时设计了全局积分滑模自适应反步控制器，以实现系统的动态解耦和分散控制；文献[7]将ADRC技术应用于板宽板厚双输入双输出不确定大时滞系统的控制，解耦后各通道分别按常规的单变量时滞系统来设计，并通过ESO估计并补偿模型摄动造成的静态解耦不匹配和通道间的动态耦合，仿真结果表明，该系统鲁棒性能及解耦效果良好；文献[8]采用ADRC技术将活套系统中高度和张力间的动态耦合作用当作各自通道上总扰动的一部分，利用ESO进行估计并给予补偿，从仿真结果来看，ESO可以对扰动、动态耦合等不确定因素进行补偿，ADRC技术的抗干扰性能等指标明显优于PID控制。

由于传统ADRC需要整定的参数较多，高自强[9]提出利用线性关系函数来处理ESO和误差反馈控制器这两个环节，将ADRC简化为线性自抗扰控制(LADRC)，并基于带宽方法确定控制器的参数。LADRC技术使系统更易于调试和实际应用，且更便于利用频率响应法来研究闭环系统的性能，这促进了ADRC理论的深入发展及其在工程中的进一步应用[10]。

基于此，本文在平整机板形板厚二阶系统综合控制研究的基础上，采用线性扩张状态观测器(LESO)估计系统总扰动，并设计了采用PD控制律下的LADRC控制系统，结合对外部扰动和模型参数摄动条件下的仿真实验，验证了该控制策略的有效性。

1 平整机板形板厚系统模型

平整轧制的主要目的是祛除带钢退火后的屈服平台，改善带钢板形板厚质量。延伸率表示法作为板形定量表示法中最常用的一种，其控制手段主要包括平整机辊缝形成的压力(平整力)和张紧辊区域的带钢张力。对于来料厚度不同的带钢，延伸率可以通过改变两者的受控关系来获得，即：①对于厚度超过1.0 mm的带钢，延伸率的控制是以控制平整力为主、张力调节为辅的，较大影响的是带钢厚度；②对于厚度在1.0～0.35 mm之间的带钢，延伸率可以由平整力和张力联合控制；③对于厚度在0.35 mm以下的带钢，延伸率控制则是以张力调控为主、平整力调节为辅的，较大影响的是带钢板形[2]。当调整压下时，主轧机的前后滑作用会影响张力；当调整张力时，变形区的应力状态又会影响到带钢的厚度与板形。由此可见，平整轧制板形板厚控制模型是具有强耦合作用的多变量系统，该系统的工作示意图见图1。

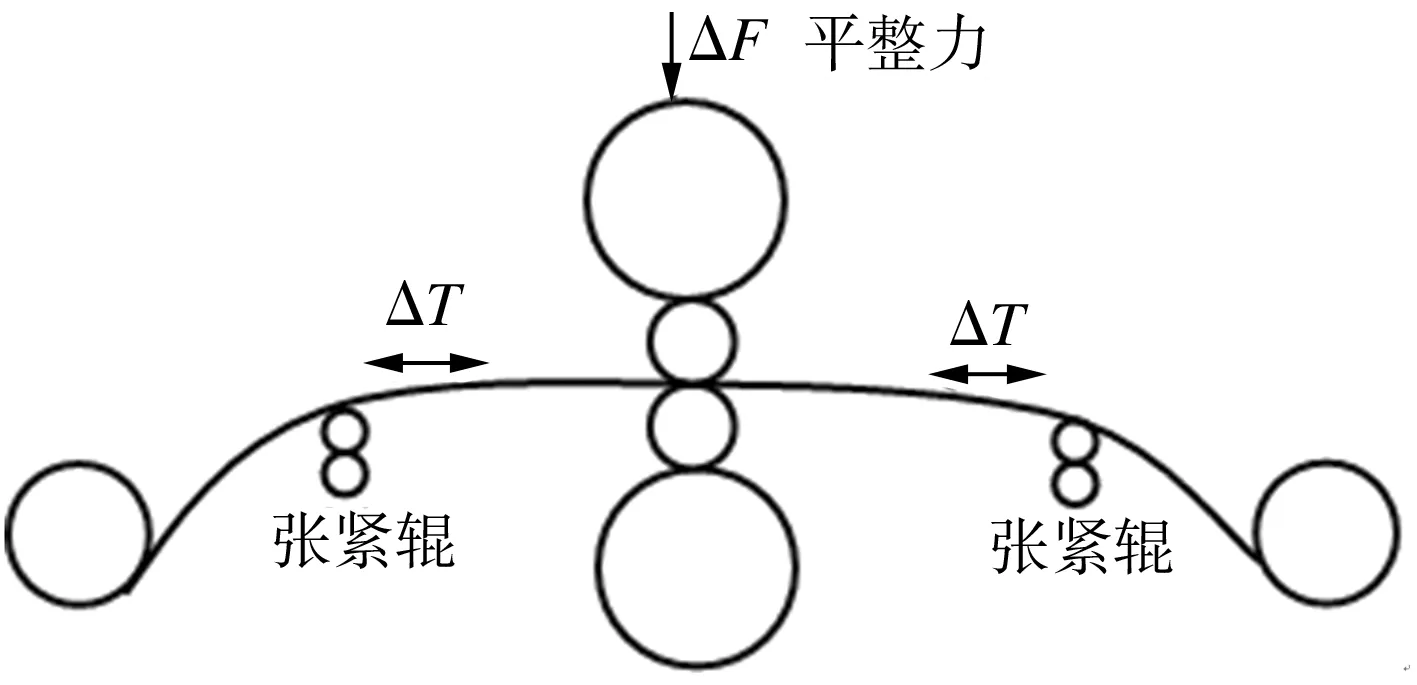
图1 平整力与张力联合作用示意图

Fig.1 Schematic diagram of the joint action of temper rolling force and tension force

参照文献[2-3]，实际平整机板形板厚控制系统的模型辨识后，归纳得到被控制对象的等效传递函数为：

(1)

在此基础上，得到某轧钢厂1450 mm平整机板形板厚数学模型为：

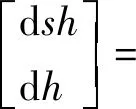
(2)

式中：dsh为平整带材延伸率的变化量；dh为平整带材厚度的变化量；T为带材所受张力；F为平整机的平整力；φ和δ分别表示模型系数的变化量。

令y1=dsh，y2=dh，则式(1)可写成：

(3)

将式(3)中G12(s)u2(s)和G21(s)u1(s)视为y1(s)、y2(s)的外部扰动，其时域值分别为w1、w2，表示成微分方程形式为：

(4)

式(2)是在平整工作速度为10 m/s的相对静态工作点时所建立的，而当平整速度在8～12 m/s区间变化时，静态模型中各参数会有摄动，主要体现在式(2)中参数δ、φ。图2所示即为参数δ在-225～+225、φ在-120～+120范围内摄动时耦合模型的幅相频率特性，图3为输入1和输入2同时给定单位阶跃激励信号时耦合模型摄动后的响应。从图2和图3中可以看出，由于受到参数摄动的影响，系统在交叉通道的耦合作用尤为明显。由此可见，需要设计控制器使得系统获得比较理想的动静态性能，同时又达到解耦控制的目的。

图2 参数摄动下耦合模型的幅相频率特性

Fig.2 Amplitude phase frequency characteristics of coupled model with parameter perturbation

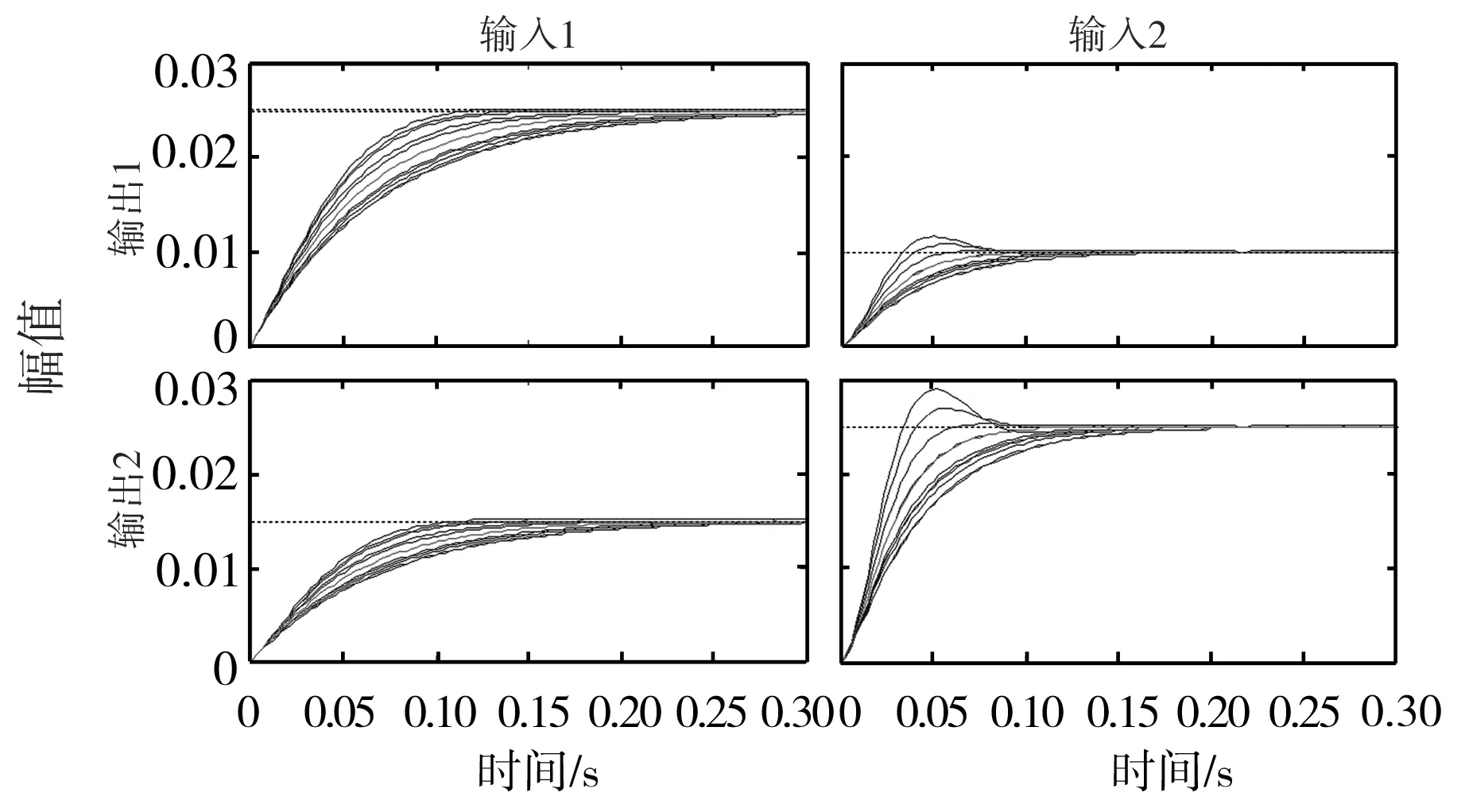
图3 参数摄动下耦合模型的阶跃响应

Fig.3 Step response of coupled model with parameter perturbation

2 系统控制器设计

设二阶系统

(5)

(6)

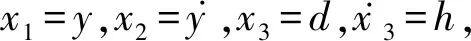
(7)

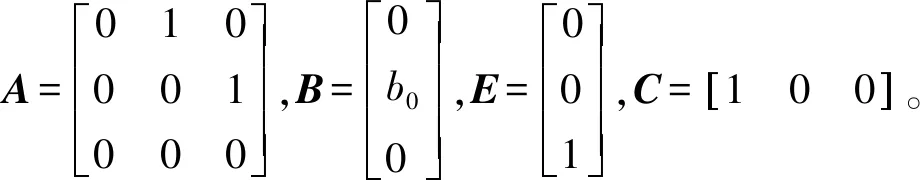
亦即

(8)

利用LESO来估计系统的总扰动，设计观测器如下：

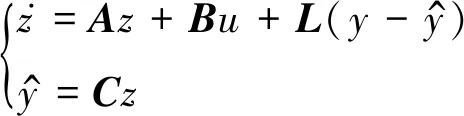
(9)

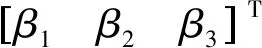
(10)

b0u≈z3+b0u=u0

(11)

采用如下控制规律

(12)

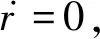
(13)

则

(14)

(15)

3 仿真实验研究

以式(2)对应的系统为仿真实验的研究对象，利用Matlab数学软件完成对控制系统的分析和鲁棒控制器的求解。构建的LADRC结构框图如图4所示。

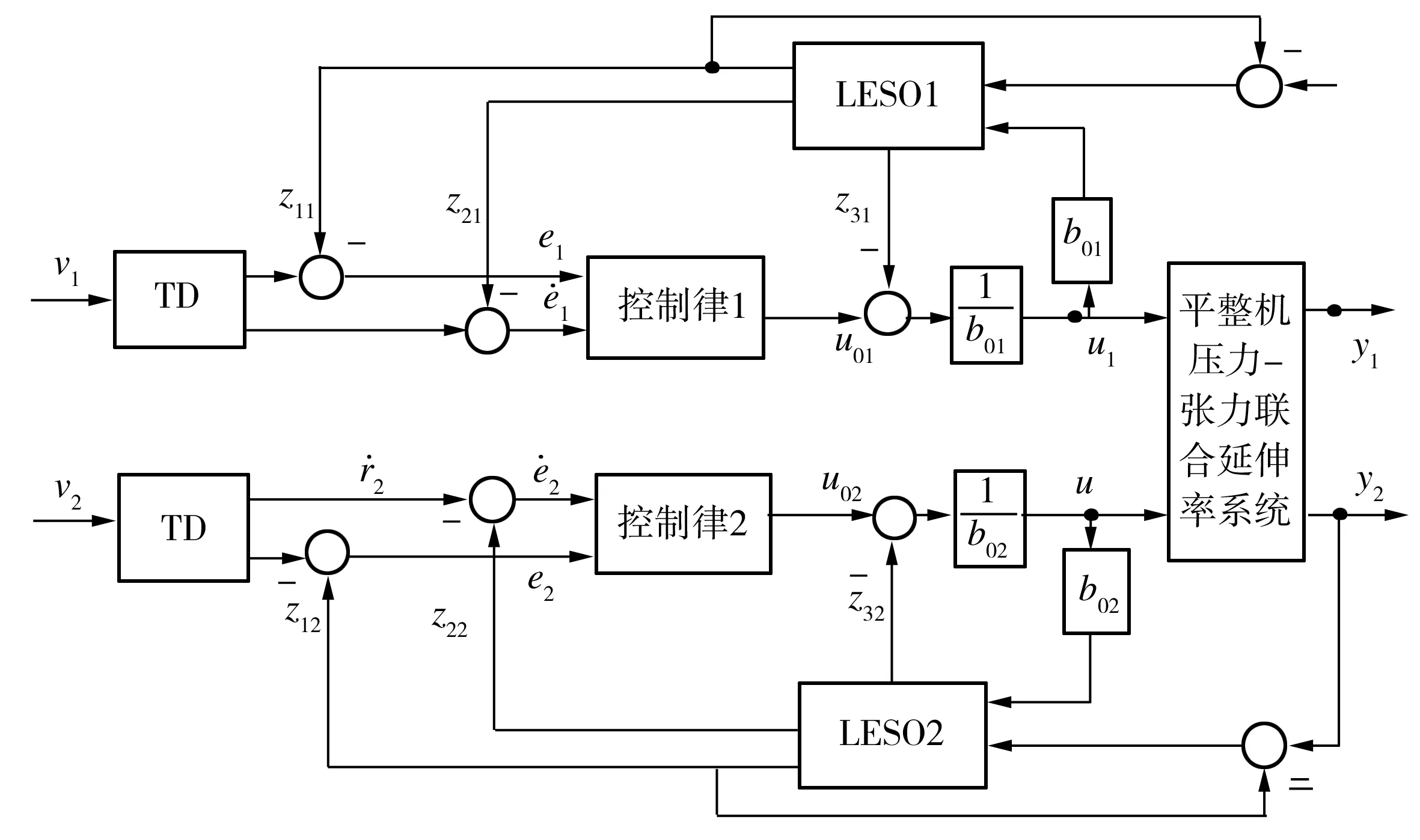
图4 LADRC结构仿真图

根据文献[9]提出的带宽法实现调整控制器带宽wc、控制器阻尼比ξ及观测器带宽w0，在满足控制系统性能条件下选定wc、ξ值，然后再调整w0，使其达到LADRC系统稳定。

当式(2)中δ、φ均为0即模型参数不变时，系统的响应曲线如图5所示。t=2 s时在y1的量测端附加上0.05幅值阶跃扰动，t=3 s时在y2端加入0.05幅值阶跃扰动，得到系统的响应曲线如图6所示。当δ=225、φ=120，即模型参数变化50%时，在量测端加入扰动后系统的响应曲线如图7所示。从图5～图7可以看出，该系统响应速度较快，并且在实现解耦的同时，也对外部扰动和模型参数摄动具有较好的抑制作用。

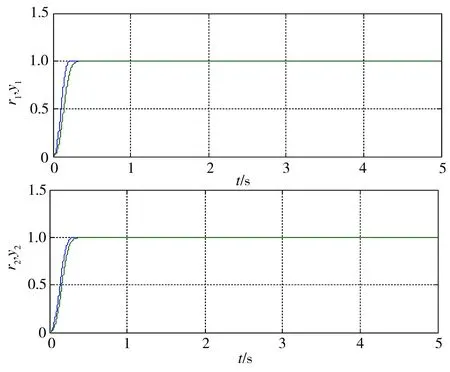
图5 无扰动时系统的响应曲线

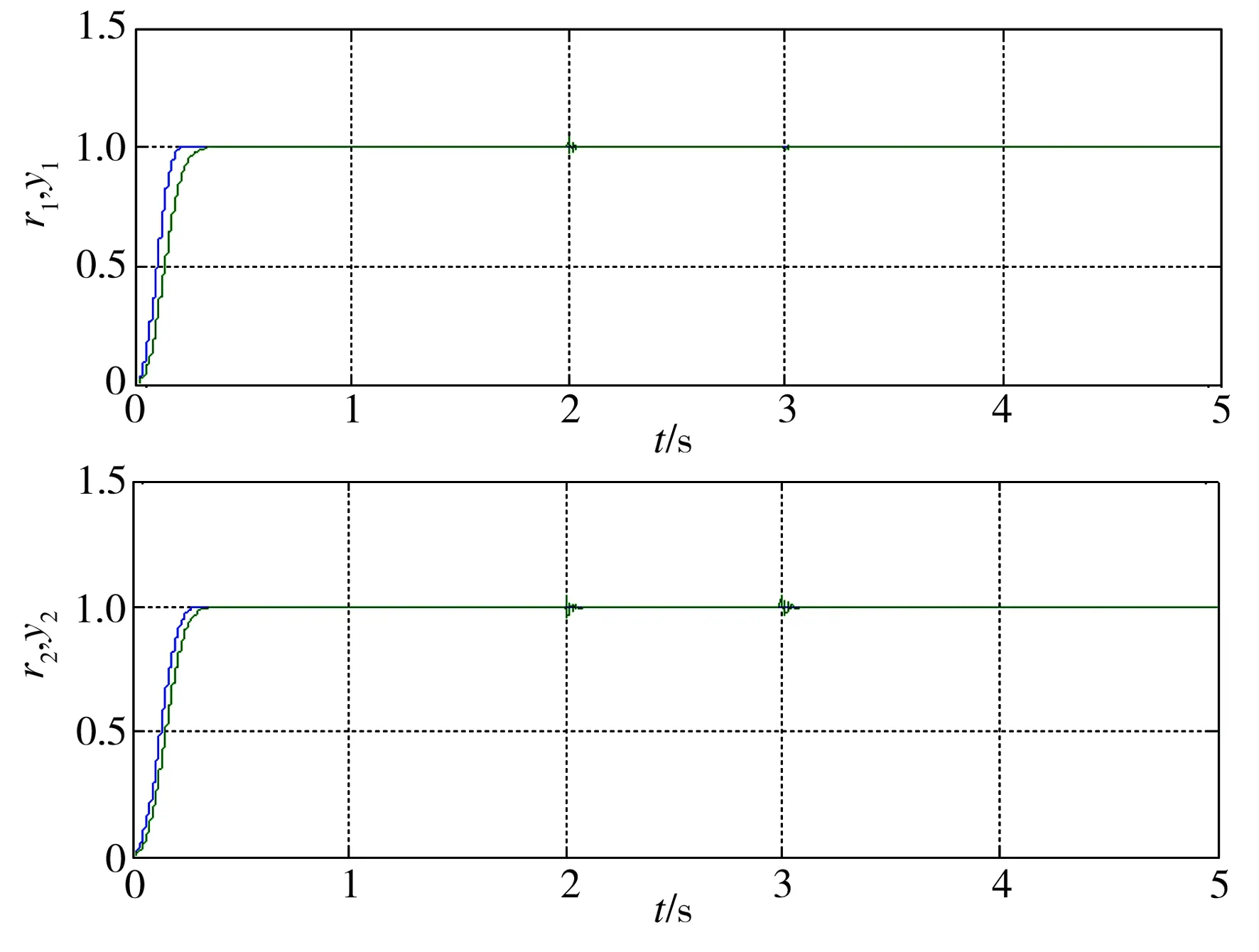
图6 在系统输出量测端加入扰动时系统的响应曲线

Fig.6 Response curves of system when disturbance is added on the measurement end of system output

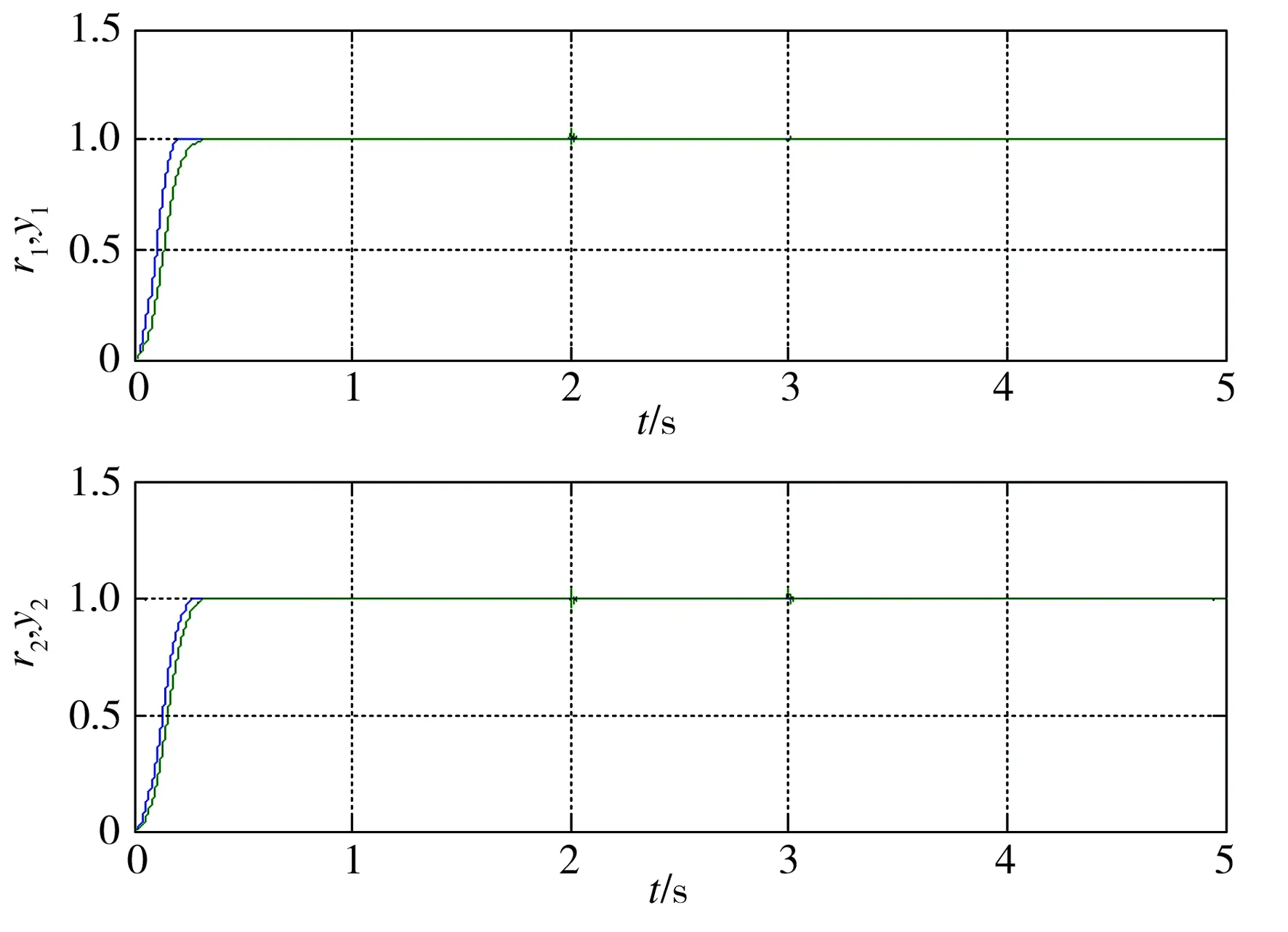
图7 参数波动50%时系统的响应曲线

Fig.7 Response curves of system with 50% parameter fluctuation

4 结语

本文将LADRC技术应用于平整机板形板厚耦合系统的控制，将模型参数摄动造成的静态扰动和外部的动态扰动作为总扰动，通过线性扩张状态观测器(LESO)进行估计与补偿，并在状态反馈PD控制率下进行了仿真分析，结果表明，控制系统在获得解耦效果的同时，还获得了良好的动态性能和鲁棒性，研究结果为LADRC技术的实际应用奠定了基础。