基于CNN-SVM的深度卷积神经网络轴承故障识别研究

胡晓依， 荆云建， 宋志坤， 侯银庆

(1.中国铁道科学研究院 铁道科学技术研究发展中心，北京 100081；2.北京交通大学 机械与电子控制工程学院，北京 100044)

基于数据驱动的智能诊断主要是通过机器学习方法对由信号处理得到的故障特征进行分类识别，常用的识别算法有：支持向量机(Support Vector Machine, SVM)、人工神经网络(Artificial Neural Network，ANN)、邻近1算法(k-Nearest Neighbor，KNN)等，识别效果取决于故障特征能否准确地反映出故障类型的本质区别，虽然传统智能诊断取得了重要成果，但基于模式识别的“浅层网络”模型表达能力有限、泛化能力不足，且依赖于信号处理技术和故障诊断经验[1]。而深度学习模型有强大的表达能力，将特征提取与分类识别融为一体，降低对信号处理技术依赖的同时也满足了工业大数据背景下海量、高维数据的分析需求[2]。近年来国内外学者对深度学习应用于故障诊断已作出一些研究，如Jia等[3]针对不平衡样本数据集，通过正则化权值、加权损失函数等改进卷积神经网络，对非平衡样本下的滚动轴承故障进行识别，并且对卷积核的物理意义作了探究；Shao等[4]提出改进的压缩感知卷积深度置信网络用于滚动轴承振动信号的特征学习与故障识别，使用压缩感知减少振动数据量以提高分析效率，再通过高斯可见单元构建CDBN模型对轴承故障进行分类识别；袁建虎[5]提出基于小波时频图和卷积神经网络的诊断方法，对振动信号进行连续小波变换得到以灰度图显示的时频图作为故障特征，通过卷积神经网络识别滚动轴承故障。王丽华等[6]使用短时傅里叶变换将振动信号转换为时频图后通过卷积神经网络识别异步电机故障，取得了理想的识别效果，基于深度学习理论建立故障诊断模型的研究已初见成效,但均存在计算量庞大、模型复杂度高、模型训练较困难等问题。

本文使用深度学习的经典算法-卷积神经网络(Convolutional Neural Network，CNN)，并将支持向量机融入模型，引入深度学习的模型优化技术，提出适于轴承故障诊断的CNN-SVM深度卷积神经网络模型，模型直接作用于原始实测轴承振动信号，自适应地从原始数据中逐层学习故障特征，模型顶层分类器实现不同故障的精细化识别，文中引入批量归一化(Batch Normalization，BN)与dropout等模型优化技术配合改进型的SVM分类器，来提升模型的收敛速度与泛化能力。

1 CNN卷积神经网络架构与算法原理

1.1 卷积层与池化层

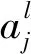
池化层又称下采样层，对卷积得到特征图做进一步压缩，以均值池化和最大值池化最为常见，池化层的计算公式如式(3)所示，本文拟采取最大值池化方式。

(1)

(2)

(3)

1.2 全连接层与SVM分类器

卷积池化后的特征图进入全连接层进行分类，首先需将卷积后的特征图光栅化为一维向量，使得局部特征在更高维度上进行全局信息整合。

针对滚动轴承一维振动信号和数据集样本数量较少的问题，本文引入针对小样本数据分类效果更为稳定的SVM分类器。SVM是建立在统计学习理论和结构风险最小化原理基础上的机器学习算法，通过定义适当的核函数实现非线性变换将输入空间变换到线性可分的高维空间，找到高维空间的最优线性超平面[7]。传统支持向量机解决二分类问题，而针对滚动轴承不同故障部位和不同故障程度的多分类问题，可采用“一对多”、“一对一”和“有向无环图”等方法实现多分类，本文拟采用“一对一”法，即针对N类样本，每两类样本训练一个子分类器，共构造N(N-1)/2个子分类器，在预测新样本所属类别时每个子分类器都对其进行判别并为相应类别“投得一票”，最后决策阶段以获得票数最多的类别作为被识别样本的类别。

1.3 模型目标函数与训练算法

监督学习中，引入目标函数(Loss函数)来评价输入数据经模型后的输出值与期望值的一致性程度，引入式(4)所示的平方折叶损失函数，为抑制数值较大的权值，提升模型的泛化性，引入式(5)所示正则化惩罚项，SVM多分类Loss函数合并为式(6)。

Li=∑j≠yimax(0,f(xi;W)-f(xi;W)yi+Δ)2

(4)

(5)

(6)

式中：xi为第i个样本数据，其正确标签为yi；f(xi;W)j为第j个分类经评分函数f计算的得分；Δ为边界值；W为权重；λ为惩罚强度。

Adam训练算法[8]：Adam是一种学习率自适应的优化算法，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率，在反向传播阶段，更新权值求得全局最优解，使Loss函数达到最小值。

1.4 模型优化技术

文在搭建轴承故障诊断深度卷积神经网络模型时将在全连接层引入Dropout处理，并尝试在卷积层中添加BN层，并通过实验过程来验证Dropout和BN的实际效果。

(7)

(8)

(9)

(10)

2 实验数据与信号时域分析

2.1 实验数据集

采用CWRU的滚动轴承数据集，通过电火花加工单点损伤，故障位置有内圈、外圈、滚动体，故障直径包括:0.18 mm，0.36 mm，0.54 mm。在0～3 hp四种负荷下，由12 kHz加速度传感器测得数据。同一种故障类型可能出现在不同工况、不同轴承位置中，数据集要尽可能全面地呈现轴承状态，将不同故障位置，将不同损伤程度轴承都单独看作一类，数据集共有包含正常轴承在内的10种类型，以1 024个数据点为一个样本，共8 000个实验样本，实验数据集如表1所示。

2.2 振动信号时域波形

十种不同状态的轴承振动信号时域波形如图1所示。

表1 实验数据集

图1 不同状态的轴承振动信号时域波形Fig.1 Bearing vibrations of different time-domain waveform signal state

不同类型的故障信号时域波形有较明显区别，而同种故障的不同损伤程度则难以区分，为了实现早期微弱故障的诊断与不同程度故障的精细化识别，研究基于深度学习模型的自适应特征提取方法。

3 模型搭建与实验结果分析

3.1 卷积神经网络的模型架构设计

针对1 024维的原始振动信号，设计如图2所示的“卷积-池化-卷积-池化-卷积-池化-全连接-SVM分类器”结构的模型，三层卷积池化来提取原始信号的特征。为了获得丰富的感受野[11]以提取到更多的有效特征，同时避免冗余的计算，卷积核的大小和数量须适当，逐层减小的卷积核可以有效地压缩模型的参数。模型具体参数如表2所示。

图2 模型结构示意图Fig.2 Model structure diagram

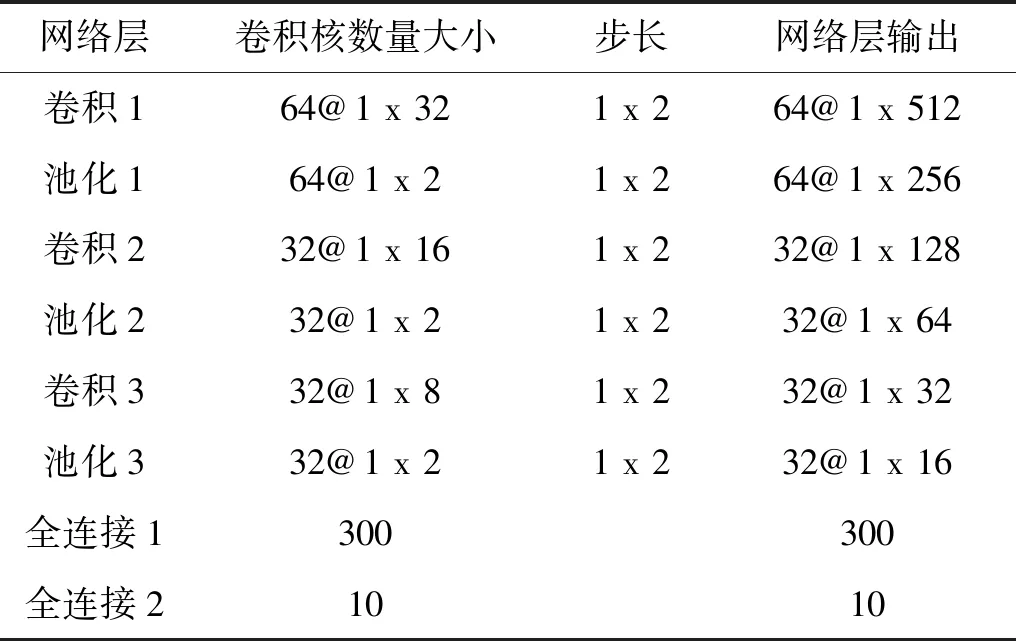
网络层卷积核数量大小步长网络层输出卷积164@1 x 321 x 264@1 x 512池化164@1 x 21 x 264@1 x 256卷积232@1 x 161 x 232@1 x 128池化232@1 x 21 x 232@1 x 64卷积332@1 x 81 x 232@1 x 32池化332@1 x 21 x 232@1 x 16全连接1 300300全连接21010

3.2 模型搭建与实验结果分析

基于Python-Tensorflow搭建模型，在Inter-i7-7700CPU，GTX1070-8 G，16 G内存的计算条件下进行实验，并在可视化工具Tensorboard中记录实验数据。

将数据集随机以6 ∶4划分训练集、测试集，实验1：使用表2参数搭建模型，使用交叉熵损失函数和Softmax分类器，超参数设置：mini-batch=100，学习率0.001，Dropout=0.75。实验2：在实验1的基础上将每层卷积得到的特征图进行批量归一化处理后再进行激活函数转换，沿用表2模型参数和实验1超参数设置。实验3：在实验2的基础上，引入SVM多分类损失函数和SVM分类器来进一步优化模型，沿用表2模型参数和实验2超参数设置，SVM的核函数采用高斯径向基函数(Radial Basis Function,RBF)，经过K折交叉验证确定惩罚因子C=8.94、核参数γ=3.26。

各实验的分类准确率和Loss函数值如图3和图4所示，实验1中训练至3 500次时，模型收敛，训练集、测试集准确率分别达到89.5%，87.1%，Loss值分别降至1.58，1.62，虽未发生过拟合，但是识别准确率较低、训练步长较多；实验2训练至2 000次时，模型收敛，训练集、测试集准确率分别达到96%，94%，同时Loss值也进一步降低至1.50，1.52，BN层的介入显著地加快了训练速度，同时准确率也有较大的提升，过拟合的风险进一步降低；实验3训练至600次时，模型已完全收敛，训练集、测试集分类准确率分别达到100%，99%，Loss值也降低至0.01，0.05。实验结果表明，采用SVM分类器配合BN层，有效地提升模型收敛速度和分类准确率，模型的泛化能力得以显著提升，为进一步说明BN层和SVM分类器对模型训练速度的提升作用，记录各实验的训练时间如表3所示，可以看出增加BN层以及使用“一对一”分类策略的SVM多分类器均会增加单步训练时长，但训练步数的有效减少则大幅度降低了总体训练时长，加快了模型的收敛速度。

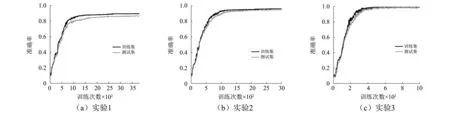
图3 准确率变化曲线Fig.3 Accuracy change curve

图4 Loss函数变化曲线Fig.4 Loss function curve

表3 各实验的训练时间

3.3 模型泛化能力验证

考虑到实际工况中，实测轴承振动信号中往往混杂大量干扰噪声，本文将研究不同噪声水平下，深度卷积网络模型的稳定性、泛化能力与强化学习下的提升能力[12]。将测试集2 000个样本全部添加不同信噪比的(SNR=-3～3)高斯白噪声，使用实验3训练好的模型来测试加噪测试集的准确率。图5为滚动体中度磨损添加信噪比SNR=-1噪声时的振动信号时、频域波形。

图5 噪声信号时、频域波形Fig.5 Noise signal time domain and frequency domain diagram

加噪测试集的分类准确率如图6所示，在噪声干扰下模型可保持较高的准确率，说明优化后的模型有着较强的抗噪声稳定性和泛化能力。

3.4 模型的强化学习能力

随机选取少量训练集样本添加不同信噪比的噪声制作如表4所示的强化训练集，经过一定次数的微调训练，测试不同信噪比下的加噪测试集准确率，得到如图7所示的准确率变化曲线，可以看出只需添加少量的噪声样本，模型可迅速学习到噪声干扰下的数据分布特征。深度学习模型拥有小样本数据微调的强化学习能力，在数据复杂多变的情况下，可不断调整和优化模型。

图6 不同噪声程度测试集的准确率Fig.6 Different noise level test set accuracy

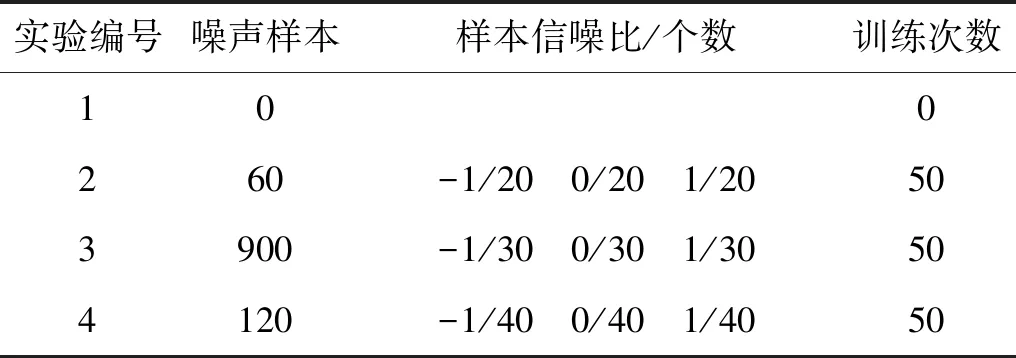
实验编号噪声样本样本信噪比/个数训练次数100260-1/20 0/20 1/20503900-1/30 0/30 1/30504120-1/40 0/40 1/4050

图7 各微调实验下的加噪测试集的准确率Fig.7 The accuracy of the noise-added test set under each fine-tuning experiment

3.5 模型性能对比

为进一步验证基于深度学习模型的轴承诊断方法的效果，将其与如下几种基于传统机器学习分类的轴承诊断方法进行对比:①按照文献[13]提出的方法，使用EMD对信号进行分解，提取信号的各阶模态特征构造SVM的输入向量；②参考赵志宏[14]提出方法，将小波分解得到的近似和细节系数计算信号的相对小波能量作为特征向量，通过SVM进行分类；③参考文献[15]提出的方法，提取波形因子、裕度因子、峭度、均方根频率、频率标准差等8个时频特征作为SVM的输入向量。

在相同计算条件下，以上述几种方法搭建模型，在测试集和加噪测试集(测试集全部添加SNR=1的高斯白噪声)上的准确率如表5所示,四种方法在不含噪声的测试集上均有较理想的准确率，但在加噪测试集上准确率远低于本文提出的诊断方法，同时相较于其他方法CNN-SVM模型的计算效率也较好。

表5 不同方法的准确率

4 结 论

(1)本文提出的基于深度学习理论的卷积神经网络模型能十分有效地进行轴承故障诊断。

(2)文中搭建的模型将特征提取与分类识别融为一体，能够直接从原始实测振动信号中通过逐层卷积学习到故障特征，实现不同故障类型的精细化识别。

(3)通过引入批量归一化、dropout处理和使用SVM分类器优化模型，可显著提升模型收敛速度与分类准确率。

(4)本文提出的诊断模型有较强的泛化性，在强烈噪声的干扰下可保持较高的分类准确率，并且具有基于小样本数据强化学习的能力，可根据所分析数据的变化不断优化模型。