改进AMD广义形态分形维数和KFCMC的液压泵故障诊断方法

2019-10-10姜万录王宝中

振动与冲击 2019年18期

郑直，姜万录，王宝中, 王莹

(1. 华北理工大学机械工程学院，河北唐山 063210； 2. 燕山大学河北省重型机械流体动力传输与控制重点实验室, 河北秦皇岛 066004；3. 燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004)

液压泵作为液压系统的重要动力元件，能持续不断地向液压系统提供压力能，因此被称为“心脏”。液压泵被广泛地应用于机械、航空、船舶、汽车、轻工、纺织、食品、电子等领域。上述领域设备已经由原来的大型连续化、集成一体化、精密自动化向人工智能化方向快速发展，而液压泵所面临的工作环境也趋向于高温、高压、高速、重负载等恶劣工况，加速了液压泵健康状态的劣化，因此对液压泵的智能故障诊断具有十分重要的意义。目前，国内外一些学者对液压泵故障诊断进行了大量研究[1-3]。

针对EMD(Experience Mode Decomposition)方法存在的问题，比如紧密频率间隔所导致的模态混叠问题，以及窄带信号分解困难和难以区分间歇性波动等问题，Chen等[4]于2012年提出了一种新型多模态信号分解方法，即解析模态分解(Analysis Mode Decomposition, AMD)。AMD能根据若干个故障特征频率先验知识，将一个非线性、非平稳多模态信号基于二分频率原则分解为两个模态分量信号和，其中一个信号为单一模态分量，另外一个信号由若干个模态分量组成。这两个信号的傅里叶谱在频域范围内是相互排斥的，且不为零。因此，AMD能够提取感兴趣特征频率信号，剔除噪声和干扰影响。目前，国内外一些学者对AMD进行了相关研究，但成果较少[5-6]。

数学形态学又称为形态学，Matheron等于1964年提出该理论，之后Maragos等[7-8]将其应用到信号处理领域。在此基础上，形成了广义形态分形维数(Generalized Morphological Fractal Dimensions, GMFD)方法，相比传统分形维数和单一形态分形维数，它能降低网格位置和尺寸变化对估计结果的不稳定影响，且能够全面和准确地反映信号的非线性和复杂程序信息[9]。

核模糊C均值聚类(Kernel Fuzzy C-means Clustering, KFCMC)是在模糊C均值聚类(Fuzzy C-means Clustering, FCMC)和k-means聚类基础上发展起来的[10]。KFCMC具有核函数，能将待分析数据从原始低维空间映射至高维特征空间，进而将划分到同一类的样本相似性增大、不同类之间的相似性减小。因此，KFCMC能实现高效和准确地识别分析。

本文重点针对液压泵的中心弹簧磨损和滑靴磨损故障诊断问题，提出一种基于改进AMD，GMFD和KFCMC相结合新方法。通过仿真信号和实测液压泵故障振动信号的实验验证，结果表明所提方法能够实现高精度的故障诊断，为故障诊断理论提供了一种高效和简捷的方法。

1 改进解析模态分解

1.1 AMD分解

(1)

(2)

式中:si(t)为基于希尔伯特变换、正弦和余弦运算得到的。

由上述可知，AMD可将x(t)分解为两个信号的和。因此，如要提取ω1频率成分信号，只需选取ω1和ω2之间值作为二分频即可实现；如要提取ωi频率成分信号，需选取ωi和ωi+1之间值作为二分频分解出的前半部分再去除选取ωi-1和ωi之间值作为二分频分解出的前半部分即可；如要提取ωn频率成分信号，只需选取ωn-1和ωn之间值作为二分频即可实现。

1.2 改进AMD分解

由上述分析可知，在有效二分频值范围内，任选一个二分频值，即可从原信号x(t)中分解出含有感兴趣特征信息的分量si(t)，而不同二分频值分解得到的si(t)含有特征信息量则不同。因此，二分频值选取的经验性和主观性对分解效果有十分重要影响。

欧氏距离反映了两个信号之间的相似性关系。基于此，为了评价分解效果，分别求取si(t)和x(t)之间的欧氏距离。如果欧氏距离越小，说明二者之间相似性越高，且si(t)含有x(t)中丰富特征信息，则信号分解越成功[11]。

因此，本文提出基于欧氏距离法自适应选取最优二分频，进而实现多模态信号的最优模态分解，为故障诊断提供高质量数据源。改进后步骤如下所示：

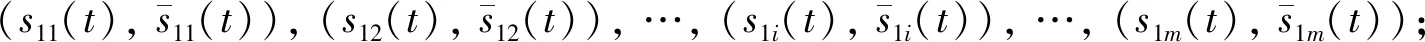
步骤2分别求取s11(t)和x(t),s12(t)和x(t), …,s1i(t)和x(t), …,s1m(t)和x(t)的欧式距离，它们分别为E1,E2,…,Ei,…,Em；

步骤3筛选出最小值Ei，则对应频率ωi即为实现最优分解效果的最优二分频，s1i(t)即为所提取的最优分解信号；

步骤4同理，可根据1.1节最后一段所提步骤提取频率为ω2,ω3, …,ωi，…,ωn的信号。

2 广义形态分形维数

f(n)为一维离散信号，其定义域为F={1, 2,…,N}。

定义划分函数为

(3)

式中：q为给定参数;λ为结构元素尺度；α(λ)为系数；ui(λ)局部度量分布函数。

因此，GMFD的表达式为

(4)

对lg[Ag(λ)/λ2]和lg[1/λ]进行最小二乘拟合，实现对Dq的估计。

3 数值仿真算例

3.1 仿真信号

仿真信号设计为

x(t)=x1(t)+x2(t)+x3(t)

(5)

x(t)=5sin(40πt)+5sin(150πt)+noise

(6)

式中:x1(t)为频率为20 Hz的正弦信号；x2(t)为频率为75 Hz的正弦信号；x3(t)为标准差为1的高斯白噪声。采样频率为2 000 Hz，采样时间为1 s。

本文针对液压泵单故障进行诊断，所以只提取含有故障特征频率的分量进行分析即可。因此，设20 Hz正弦信号x1(t)为感兴趣故障信号、75 Hz正弦信号x2(t)模拟正弦干扰信号、标准差为1的高斯白噪声x3(t)模拟强背景干扰噪声。

原信号x(t)、正弦信号x1(t)、正弦信号x2(t)和高斯白噪声x3(t)的时域，如图1所示。

图1 仿真信号Fig.1 The simulation signals

仿真的目的是为了分解出含有频率为20 Hz的正弦信号的模态分量。

3.2 基于改进AMD的仿真信号分析

基于二分频选取原则，二分频有效范围为20 Hz<ωi<50 Hz。理论上，在此有效范围内选取任一频率作为二分频即可实现对正弦信号的提取。

根据本文提出的改进思想，利用二分频率ωi分别从原信号x(t)中提取正弦信号，其分别记为s11(t),s12(t), …,s1i, …,s1m(t)，并求取它们和原信号x(t)的欧式距离，分别记为E1,E2, …,Ei, …,Em。欧氏距离分布如图2所示。

图2 仿真信号的欧氏距离图Fig.2 The Euclidean distance diagram of simulation signal

由图2可知，Emin=243.1对应于ω=21，说明基于该二分频所提取的正弦信号和原信号相似性最高。因此，ω=21即为实现最优分解的最优二分频值。

图3为基于最优二分频值所提取的20 Hz正弦信号分量。

图3 最优分解的正弦信号分量Fig. 3 The best decomposition mode of the sinusoidal signal

对比图1(b)的20 Hz正弦信号x1(t)和图3所提取的正弦信号可知，二者的形态特征具有高度相似性，且幅值没有发生畸变现象。因此，改进AMD可以有效地实现从原信号中提取20 Hz正弦信号。

3.3 基于原始AMD的仿真信号分析

为了对比分析所提AMD改进方法和原始AMD方法，按照原始AMD分解思想，主观性地在有效范围内任选一个频率ω=70从原信号中分解出20 Hz的正弦信号，分解结果如图4所示。

图4 原始AMD分解的正弦分量Fig.4 The decompostion mode of the sinusoidal signal based on original AMD

对比图1(b)的20 Hz正弦信号、图3的最优分解结果和图4的分解结果可知，图4分解出的正弦信号受到了严重噪声污染，且多处幅值发生了畸变现象。因此，原始AMD无法有效地实现从原信号中提取20 Hz正弦信号。

3.4 基于传统模态分解方法的仿真信号分析

为了对比说明所提改进AMD方法的优越性，本文将上述仿真信号进行传统的经验模态分解、集总经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)、经验模态分解(Local Mode Decomposition, LMD)、变分模态分解(Variational Mode Decomposition, VMD)分析。

3.4.1 基于EMD的仿真结果分析

将3模态组成的仿真信号进行EMD分解，可得到8个模态分量和1个剩余分量。由此可知，EMD方法出现了过分解现象。

为了得到和20 Hz的正弦信号时域形态特征最接近的模态分量，基于欧氏距离法选取距离最小值所对应的IMF5模态分量进行分析，该分量如图5所示。

图5 EMD分解的IMF5Fig.5 IMF5 of EMD

对比图1(b)的20 Hz正弦信号、图3的最优分解结果和图5的分解结果可知，IMF5的幅值发生了严重畸变现象。因此，EMD无法有效地实现从原信号中提取20 Hz正弦信号。

3.4.2 基于EEMD的仿真结果分析

将3模态组成的仿真信号进行EEMD分解，可得到11个模态分量和1个剩余分量。由此可知，EEMD方法出现了过分解现象。

同样，基于欧氏距离法可知，IMF5模态分量和20 Hz的正弦信号时域形态特征最接近，该分量如图6所示。

图6 EEMD分解的IMF5Fig.6 IMF5 of EEMD

对比图1(b)的20 Hz正弦信号、图3的最优分解结果和图6的分解结果可知，IMF5的多处幅值发生了严重畸变现象。因此，EEMD无法有效地实现从原信号中提取20 Hz正弦信号。

3.4.3 基于LMD的仿真结果分析

将3模态组成的仿真信号进行LMD分解，可得到5个模态分量和1个剩余分量。由此可知，LMD方法出现了过分解现象。

同样，基于欧氏距离法可知，PF1模态分量和20 Hz的正弦信号时域形态特征最接近，该分量如图7所示。

图7 LMD分解的PF1Fig.7 PF1 of LMD

对比图1(b)的20 Hz正弦信号、图3的最优分解结果和图7的分解结果可知，PF1的幅值发生了严重畸变现象。因此，LMD无法有效地实现从原信号中提取20 Hz正弦信号。

3.4.4 基于VMD的仿真结果分析

将3模态组成的仿真信号进行VMD分解，因此设分解模态个数K=3。同样，基于欧氏距离法可知，BLMF1模态分量和20 Hz的正弦信号时域形态特征最接近，该分量如图8所示。

对比图1(b)的20 Hz正弦信号、图3的最优分解结果和图8的分解结果可知，BLMF1虽然受到噪声污染较小，但信号多处幅值发生了畸变现象，甚至出现了端点效应，端点效应如图8(b)和图8(c)所示。因此，VMD无法有效地实现从原信号中提取20 Hz正弦信号。

图8 VMD分解的BLMF1Fig.8 BLMF1 of VMD

通过上述对仿真信号分析可知，基于欧氏距离法可有效地选取最优二分频，进而改进AMD方法能够自适应地从多模态信号中最优分解出频率为20 Hz的正弦信号x1(t)，所提取分量含有原信号中丰富的感兴趣特征信息。因此，改进AMD较原始AMD，EMD，EEMD，LMD和VMD具有有效性和优越性。

4 液压泵故障信号分析

4.1 实验方法

为了验证所提改进AMD方法的有效性和优越性，以柱塞数为7的MCY14-1B型斜盘式轴向柱塞泵为实验对象，利用50 kHz的采样频率采集中心弹簧磨损和滑靴磨损的Z轴振动信号，其中额定转速为1 470 r/min，泵出口压力调定为10 MPa。实验系统图如图9所示。

4.2 中心弹簧磨损单故障信号分析

截取0.6 s数据进行分析，图10为中心弹簧故障信号。

图10 中心弹簧磨损故障信号Fig.10 The signal of central spring wear fault

中心弹簧磨损故障特征频率为24.5 Hz。根据本文提出的改进思想，利用有效范围内的二分频率ω(>24.5 Hz)分别从中心弹簧磨损单故障原信号中提取中心弹簧磨损故障信号，并分别求出提取的故障信号和原信号之间的欧氏距离。上述欧氏距离如图11所示。

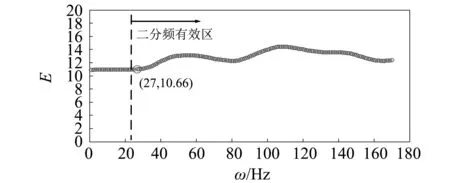
图11 中心弹簧磨损故障信号的欧氏距离图Fig.11 The Euclidean distance diagram of central spring wear fault signal

由图11可知，Emin=10.66对应于ω=27，说明基于该二分频所提取的中心弹簧磨损故障信号和中心弹簧磨损单故障原信号相似性最高，该分量含有原信号中大量故障特征信息。因此，ω=27即为实现最优分解的最优二分频值。

4.3 滑靴磨损单故障信号分析

截取0.6 s数据进行分析，图12为滑靴磨损故障信号。

图12 滑靴磨损故障信号Fig.12 The signal of slipper wear fault

滑靴磨损故障特征频率为171.5 Hz。根据本文提出的改进思想，利用有效范围内的二分频率ωi(>171.5 Hz)分别从滑靴磨损单故障原信号中提取滑靴磨损故障信号，并分别求出提取的故障信号和原信号之间的欧氏距离。上述欧氏距离如图13所示。

由图13可知，Emin=12.25对应于ω=212，说明基于该二分频所提取的滑靴磨损故障信号和滑靴磨损故障原信号相似性最高，该分量含有原信号中大量故障特征信息。因此，ω=212即为实现最优分解的最优二分频值。

图13 滑靴磨损故障信号的欧氏距离图Fig.13 The Euclidean distanc diagram of slipper wear fault signal

4.4 基于改进AMD的广义形态分形维数提取

将正常信号、改进AMD所提取的中心弹簧磨损故障信号和滑靴磨损故障信号作为数据源，提取GMFD作为特征向量，参数q设为[-20∶2∶20]，单位结构元素设为(0 0 0)，尺度参数范围设为2～35。结果如图14所示。

图14 基于改进AMD的GMFD分布图Fig.14 The GMFD diagrams based on improved AMD

正常信号接近于随机噪声，所以其形态特征具有随机性；所提取的中心弹簧磨损故障信号和滑靴磨损故障信号形态特征具有明显的周期性冲击特征。因此，基于正常信号所提取的GMFD较基于故障信号所提取的值要大[12]。

在图14中，当0≤q≤20时，正常信号和故障信号的GMFD之间都不存在混叠现象，且正常状态的GMFD值也较中心弹簧磨损故障和滑靴磨损故障的值大；当-20≤q<0时，正常状态和中心弹簧磨损故障的GMFD不存在混叠现象，且正常状态GMFD值也大，但正常状态和滑靴磨损故障的GMFD存在混叠现象。

为了说明所提方法的优越性，本文还将原始AMD,EMD,EEMD,LMD和VMD对信号进行分解，并基于欧氏距离法选取最小距离所对应分量作为数据源，并提取GMFD作为特征向量。针对原始AMD的提取，按照二分频选取原理，在有效范围内主观性地分别将中心弹簧磨损故障和滑靴磨损故障的二分频设为ω=50 Hz和ω=260 Hz。结果如图15～图19所示。

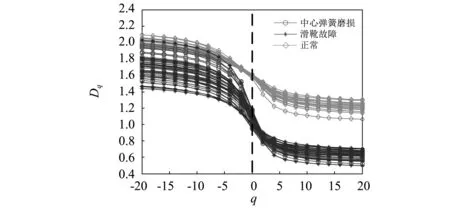
图15 基于原始AMD的GMFD分布图Fig.15 The GMFD diagrams based on original AMD

图16 基于EMD的GMFD分布图Fig.16 The GMFD diagrams based on EMD

图17 基于EEMD的GMFD分布图Fig.17 The GMFD diagrams based on EEMD

图18 基于LMD的GMFD分布图Fig.18 The GMFD diagrams based on LMD

图19 基于VMD的GMFD分布图Fig.19 The GMFD diagrams based on VMD

由图15～图19可知，在-20≤q≤20，三种运行状态的GMFD都存在不同程度的混叠现象。

基于上述，可得结论：①只有针对改进AMD分解后的信号，在q≥0时所提取的GMFD能够定量和全面地表征液压泵运行状态的非线性信息；②改进AMD可以有效地提取丰富故障特征信息，并基于最优二分频可实现最优分解，且较原始AMD,EMD,EEMD,LMD和VMD具有有效性和优越性。

5 液压泵故障诊断分析

5.1 基于KFCMC的液压泵故障诊断

对基于上述数据源所提取的GMFD作为特征向量，利用KFCMC进行液压泵正常、中心弹簧磨损故障和滑靴磨损故障诊断，其中每种运行状态含有21个样本。分类系数S和平均模糊熵E用于评价聚类质量，其中S越接近1和E越接近0，说明聚类质量越好[13]。聚类结果如表1所示。

表1 KFCMC的聚类结果

由表1可知，基于改进AMD的方法可以完全识别正常、滑靴磨损和中心弹簧磨损三种运行状态的63个所有样本，诊断率为100%；基于原始AMD的方法无法全部识别三种运行状态的所有样本，尚存在15个样本无法正确识别，诊断率为76%；基于传统EMD,EEMD,LMD和VMD的诊断方法也无法全部识别三种运行状态的所有样本，分别存在19,22,19和16个样本无法正确识别，诊断率为73%,65%,69%和75%。

5.2 基于FCMC的液压泵故障诊断

同样，利用FCMC对上述每种运行状态的21个样本进行故障诊断。聚类结果如表2所示。

表2 FCMC的聚类结果

由表2可知，基于改进AMD的方法可以完全识别正常、滑靴磨损和中心弹簧磨损三种故障的63个所有样本，诊断率为100%；基于原始AMD的方法无法全部识别三种运行状态的所有样本，尚存在16个样本无法正确识别，诊断率为75%；基于传统EMD,EEMD,LMD和VMD的诊断方法也无法全部识别三种运行状态的所有样本，分别存在19,25,22和18个样本无法正确识别，诊断率为70%,60%,65%和71%。

对比表1和表2可知，基于改进AMD所提取的GMFD能够完全被KFCMC和FCMC诊断出，且效果明显优于原始AMD及传统模态分解方法；基于相同数据源所提取的GMFD作为特征向量，KFCMC的诊断正确率要高于FCMC。