基于行为识别和曲率约束的车辆轨迹预测方法研究*

谢 枫，娄静涛，赵 凯，齐 尧

（1.陆军军事交通学院，天津 300161； 2.军事交通运输研究所，天津 300161）

前言

对驾驶人决策特性的研究表明，诸如自车与周围运动车辆的相对速度、相对距离等因素会极大地影响驾驶员的决策［1］，进而影响行车安全。对于驾驶环境中的静态车辆，智能车可安全地沿规划的轨迹行驶，对于动态车辆，人类驾驶员可以利用过去的经验和直觉预测其他驾驶员的行为来避免潜在的事故［2］，而智能车需要通过实时预测其周围运动车辆的轨迹，提高其行驶安全性。

目前在车辆轨迹预测方面，主要的方法有基于物理运动模型的轨迹预测、基于驾驶行为的轨迹预测和基于意图识别的轨迹预测等方法［3］。彭曲等［4］根据城市交通网络，依靠统计并利用历史轨迹，提出了基于马尔可夫链的轨迹预测，但预测准确率较低，仅在40%左右。Gambs等［5］提出了高阶马尔可夫模型的轨迹预测方法，精度较高，但是计算开销大，目前很难满足智能车的实时性要求；Wiest等［6］提出了VGMM用于车辆长期运动预测，但该方法仅在模拟环境中进行了测试，而且需要输入很长一段时间的历史轨迹信息。乔少杰等［7］运用卡尔曼滤波设计了动态轨迹预测算法，但预测轨迹的平均误差为12.5 m，误差较大。张金旺等［8］分别采用统计距离和马尔科夫链对车辆横向运动（垂直于车前进方向）和纵向运动（车前进方向）进行轨迹预测，但其算法在3 s内平均预测误差为2.5 m，平均耗时为93 ms，误差与耗时都较高。Schubert［9］等对目标跟踪的不同运动模型做了比较，CTRA模型在城市环境和高速公路环境下都给出了较好的结果。Berthelot［10］和Tmake［11］等利用CTRA模型来预测车辆轨迹。

为对运动车辆轨迹做出更准确地预测，本文中提出了一种基于行为识别和曲率约束的车辆轨迹预测方法，该方法将车辆运动分解为沿车道线方向（纵向）的运动与垂直于车道线方向（横向）的运动。首先接收感知得到的环境车辆信息，包括车辆的位置、速度、加速度、航向角和横摆角速度，结合高精度地图提供的车道线信息和车辆的速度、横摆角速度信息，对车辆进行行为识别；然后依据行为识别结果、车辆的位置、速度和加速度，确定车辆在横、纵向上的初始状态和结束状态，再根据运动状态分别建立横、纵向多项式方程预测其在横、纵向的运动；最后，以高精度地图中的车道线曲率作为约束，筛选出一条最优的预测轨迹。算法处理过程平均耗时为0.103 ms，满足智能车实时性的要求。若智能车周围不存在运动车辆则不进行预测。方法的流程框图如图1所示。

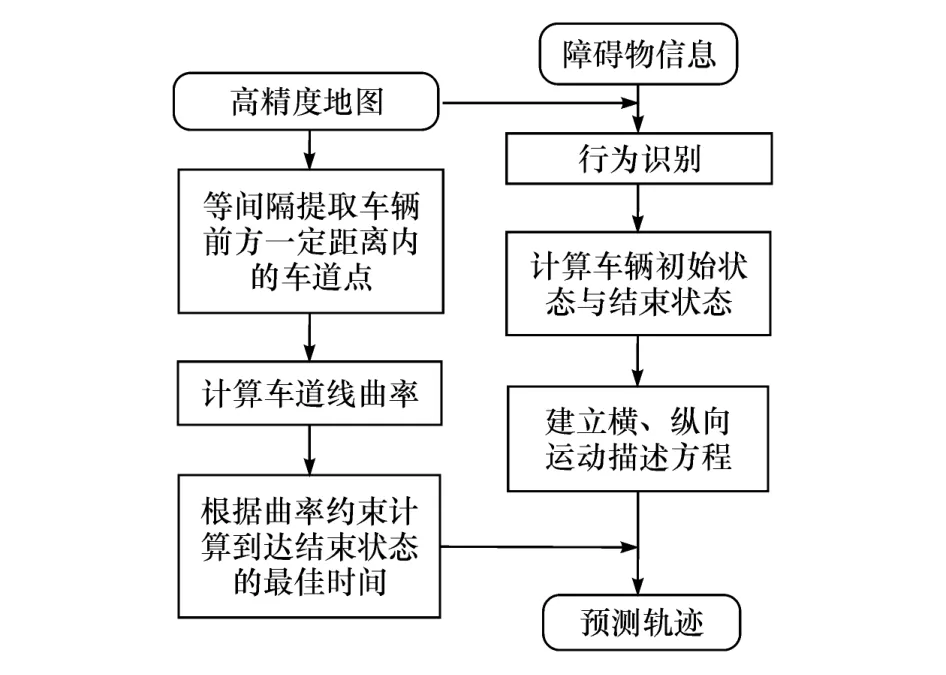
图1 本文中方法流程框图

1 车辆行为识别

通常车辆在车道上行驶时，有3种基础的行为：车道保持、换道和转弯。其它行为可由这3种行为中的几种组合得到。对于保持当前车道行驶的车辆，驾驶员一般是沿着车道中线居中行驶或是在当前车道“平行”车道线行驶；对于换道或是转弯的车辆，在一般情况下，驾驶员会寻求最小的当前机动持续时间，同时考虑到车辆乘坐人员的舒适性，车辆的横向加速度不会太大，而且实际轨迹也会比较平滑。

行为识别是利用感知得到的障碍物信息和高精度地图信息实现的，其主要步骤如下。

（1）接收并存储感知传入的当前时刻车辆的状态向量 X=［x，y，θ，v，a］T，其中，x，y是由感知得到的目标车辆在大地坐标系下的位置（此处假设车辆做平面运动，不考虑其在z轴方向的运动），θ为车辆的航向角，v，a则分别是车辆当前时刻的速度和加速度。

（2）结合高精度地图，沿车道线方向为纵向（即s坐标轴），垂直于车道线的方向为横向（即l坐标轴）建立如图2所示的s-l坐标系。每条车道线的起点处s=0，在车道中线上l=0。

（3）结合高精度地图信息以及车辆当前状态和历史状态信息，识别车辆行为。主要有3种方法：

a.根据车辆当前状态信息，计算其在横向的速度分量vl，根据vl的大小和方向判定车辆将要做出的行为；

图2 s-l坐标系

b.结合高精度地图信息，在接近路口处判断车辆所处车道的车道类型，以此判定车辆将要做出的行为；

c.利用车辆当前状态信息和历史状态信息，计算车辆的横摆角速度ω，根据横摆角速度大小识别车辆行为。

2 车道线曲率约束

高精度地图作为智能车发展的重要支撑，在精确定位、基于车辆模型的驾驶决策辅助、障碍物检测和避让等方面发挥着重要作用，是自动驾驶的核心技术之一［12］。高精度地图不仅有准确的坐标，还能准确地描绘道路形状、车道线、车道中心线等信息［13］。

高精度地图中车道（lane）是由车道线组成，车道线是由车道线段（lane segment）组成，车道线段则是由车道点（lane point）组成。首先以车辆当前时刻的位置为起点，根据车辆的速度选择车辆当前所在车道前方一段距离，然后沿车道线方向（即纵向），在给定距离内从起点开始每隔一定距离取一个车道点，得到车道点集合｛LanePoint（n），n=0，1，2，…｝。根据曲率计算公式，求出每两个车道点之间的曲率。不同的曲率意味着不同的车速，曲率越大速度越低。再根据曲率对速度做插值运算，得到结束状态时车辆的速度。曲率由以下公式得到：

式中：Δα为两个车道点所属车道线段的角度差值；Δs为两个车道点之间纵向位移之差（由于选取的两点之间距离较近，近似认为是弧长）。

本文中方法基于高精度地图建立，所使用的高精度地图为实验室自主研发，精度在厘米级，其主要制作过程有以下几个步骤：

（1）使用三维激光雷达采集点云数据，并对点云数据进行预处理；

（2）点云配准和后处理；

（3）生成反射率地图；

（4）使用JOSM软件绘制高精度地图。

由于所采用的高精度地图中的车道线为人工描绘，并不够平滑，所以本文中所用曲率与车速极值的对应关系与实际相比有所不同，其对应关系如表1所示。

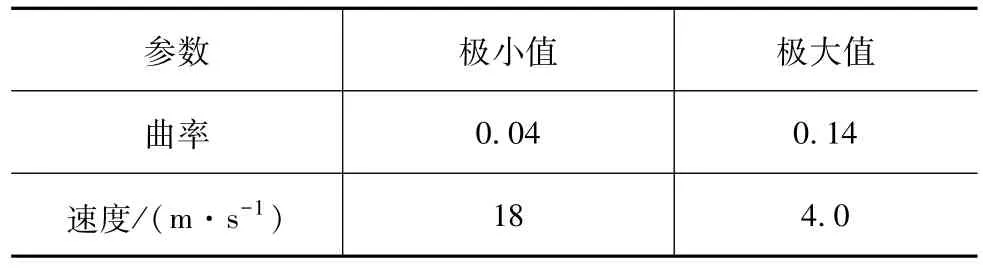
表1 曲率与车速极值对应表

3 车辆轨迹预测方法

3.1 初始状态

由于感知得到的障碍物信息是基于笛卡尔坐标系的，而行为识别中的多项式方程是以s-l坐标系为基础建立的。所以需要进行坐标系的转换，转换公式如下：

式中：l0为车辆初始状态时相对于其所在车道的横向位移；s0为车辆初始状态时相对于其所在车道的纵向位移；θsg为车辆位置点所属车道线段的方向；p为由车辆位置点所属当前车道线段的起点指向车辆位置点的向量；d为车辆位置点所属车道的有向线段；ssum为车辆位置点所属车道线段相对于当前车道起点的纵向位移。

3.2 结束状态

假设车辆在保持或改变行为的过程中，其加速度恒定，根据行为识别结果，可以得到结束状态时车辆的状态：

对于到达结束状态时，预测车辆在车道中心线上运动的行为，可令l′=0；而对于车辆会在预测车道上“平行”车道线行驶的行为，可以结合车辆的初始运动状态，改变l′的值即可。

对于行为识别结果为保持车道或换道的行为，认为车辆在纵向做匀变速运动，即t，行为识别结果为转弯行为时，认为车辆在纵向做匀速运动，即

3.3 横向运动描述

由于车辆横向运动的初始状态与结束状态都可根据行为识别结果确定，所以可建立一个与时间有关的5次多项式来描述车辆的横向运动：

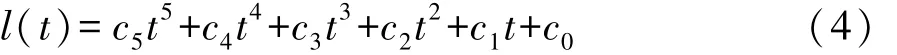
给定起始时间t0=0。由于多项式有4阶导，保证了车辆在横向的加速度是连续的。多项式的系数可由以下等式求得：

式中：t0为起始时间；t1为结束时间。

3.4 纵向运动描述

由于车辆纵向运动中结束状态的s1无法根据行为识别结果确定，所以可建立一个与时间有关的4次多项式来描述车辆的纵向运动：

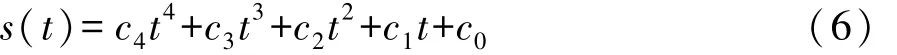
由于多项式有4阶导，保证了车辆在纵向的加速度是连续的。多项式的系数为

所有被调查者中，41.7%的学生不清楚本、专科护理的差别。在临床中，本专科学历的护士工资相差不大，工作分工也无太大差别。不少学生认为，专科生学年制为三年制，而本科生则为四年或者五年，在学年制比专科生多了一到两年的时间，然而转到临床之后，本、专科生基本上处于同等地位，至少在学历和薪酬方面没有体现出足够的优势。专业基础知识也只能说比专科生更深入全面，却缺少了更具本科学历特色的内容。

3.5 轨迹选择

通常，在结构化道路下，当车辆需要改变行为时，会考虑到车内乘坐人员的舒适性和安全性，横向速度不会太大。同时，根据驾驶习惯，驾驶员会寻求最小的当前机动持续时间。由于车辆横、纵向轨迹预测方程是关于时间t的函数，即定义车辆变换行为所需时间不同，所得到的轨迹也不同，可以认为最优轨迹的选择等价于最优时间的选择。基于此，并结合下文实验部分，正常情况下车辆变换行为在时间t=4～8 s之间较好。当然，对于不同的实验环境或条件，t会有所不同，可根据实际情况选择t的取值。认为车辆变换行为过程中加速度恒定，可得t的求解公式为

式中Δs为曲率最大点位置相对于起始车道点位置的纵向位移。

由上述描述可知，输入不同的到达结束状态所需的时间t（即t1）可得到不同的轨迹。依据上文所述车道线曲率约束条件，根据曲率与车速极值对应表得到在Δs处车辆的速度vt，结合车辆初始速度v0可求得t值。

（1）Kmax＜Cmin，认为车辆将保持当前车速行驶，此时t=4。

（2）Cmin＜Kmax＜Cmax，但 vt≥v0，认为车辆将保持当前车速行驶，此时t=4。

（3）Cmin＜Kmax＜Cmax，但 vt＜v0，利用式（8）计算时间 t，但 t应满足条件：4≤t≤8。即若计算所得 t＜4，则令t=4，若计算所得t＞8，则令t=8，其它情况直接代入t即可。其中，Kmax为预测轨迹中的最大曲率值；Cmin为表1中的曲率极小值；Cmax为表1中的曲率极大值。

最后代入t便可从一组预测轨迹中筛选出一条最优的预测轨迹。

4 实验结果与分析

为验证本文中所提方法的准确性、有效性和时间性能，采用“JJUV8”智能车为实验平台，以Velodyne HDL-64E型64线激光雷达实时采集的城市动态环境下的障碍物数据为研究对象进行实车实验。主控计算机参数为IntelRCoreTMi7-6700 CPU@3.40GHz x 8，16GB ARM，Ubuntu 16.04操作系统，Qt Creator 5.7.0开发环境，开发语言为C++，实验参数设置如表2所示。

表2 实验参数设置

分别采用本文算法与文献［10］和文献［11］中所用CTRA模型进行对比实验，对不同行为车辆进行轨迹预测。实验所选环境中的车辆较多、路况相对复杂且车辆有不同的行为，可以代表城市动态环境。本文算法预测结果如图3（a）所示，CTRA模型预测结果如图3（b）所示。图中长方体框代表感知到的动态车辆，曲线为各个车辆的预测轨迹，曲线上的点代表预测得到的车辆在未来一段时间内的具体位置。

为定量考察本文中所述方法的准确性，将预测得到的轨迹点与车辆真实轨迹点对比，进行定量评估，并计算方法耗时，验证其时间性能。

图3 两种方法轨迹预测结果

图4 ～图6分别为车辆不同行为下4 s内的轨迹预测结果。其中黑线为Velodyne HDL-64E型64线激光雷达得到的车辆位置点组成的轨迹，可认为是车辆的真实轨迹。由图可以看出，在不同行为下，虽然两种方法得到的预测轨迹都比较平滑，但本文算法得到预测轨迹更为合理，准确度更高，即利用本文算法进行的轨迹预测准确度要优于CTRA模型，验证了该算法的有效性。表3～表5分别对比了车辆不同行为下两种方法在4 s内的轨迹预测误差，实验结果取200次计算结果的平均值。对比结果表明，本文算法对车辆不同行为的轨迹预测误差更小、准确度更高。验证了该算法的准确性。

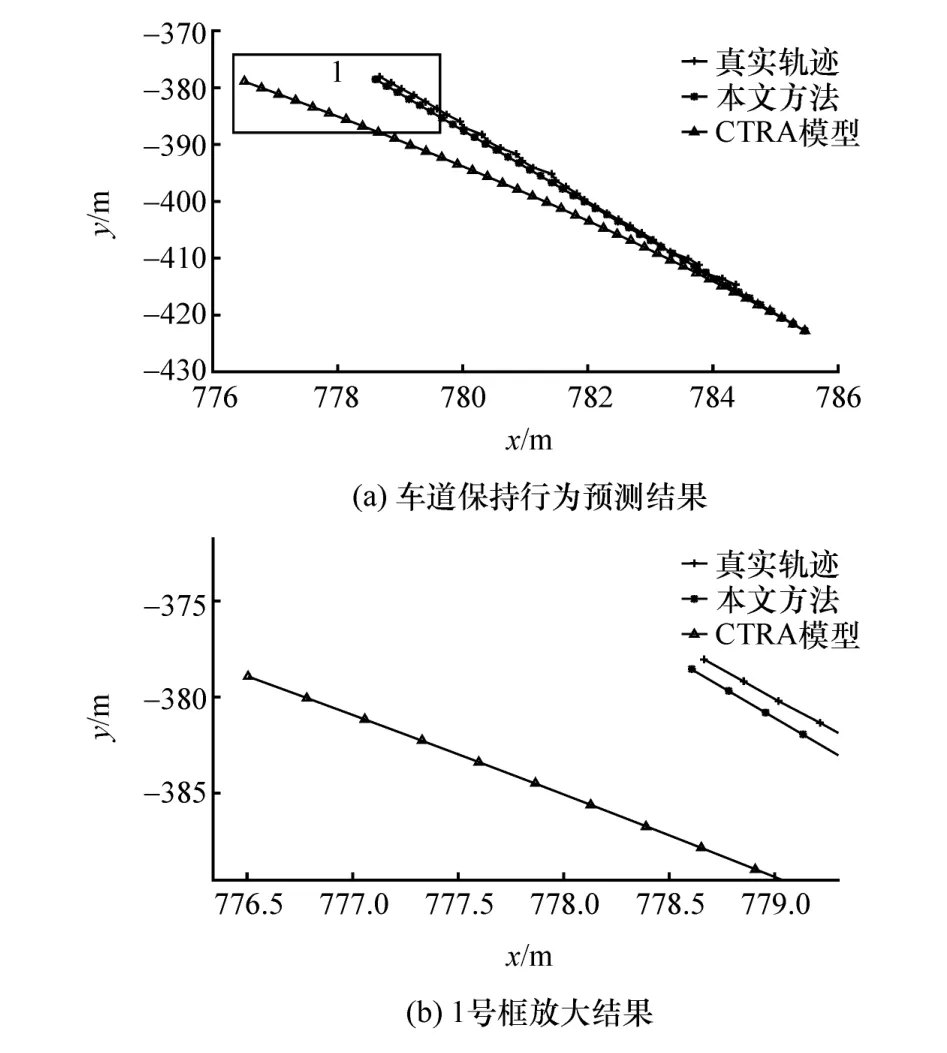
图4 车道保持行为轨迹预测结果对比

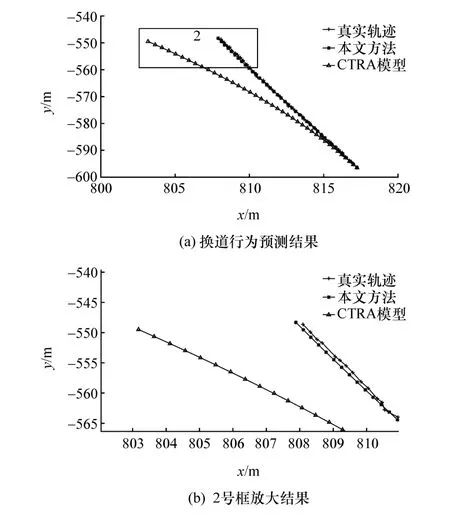
图5 换道行为轨迹预测结果对比

表3 车道保持行为轨迹预测误差

图6 转弯行为轨迹预测结果对比

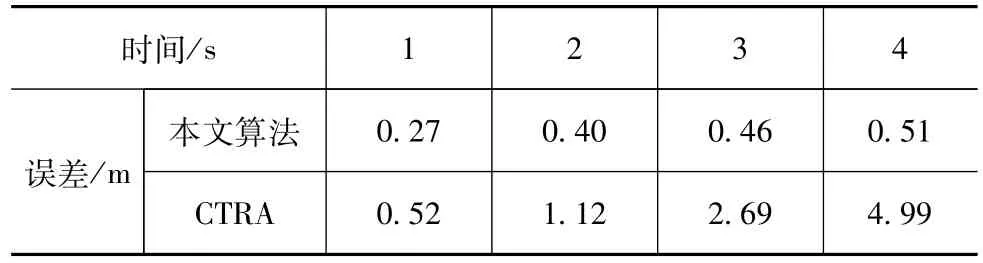
表4 换道行为轨迹预测误差

表5 转弯行为轨迹预测误差

由表3～表5可知，本文算法所得结果与车辆真实轨迹误差较小，预测的准确性较好，且预测轨迹合理。

图7为单个障碍物连续200帧两种轨迹预测方法的耗时。可以看出，虽然CTRA模型耗时相对较低，但本文方法计算时间也不高，平均耗时仅为0.103 ms，验证了本文方法的实时性。

5 结论

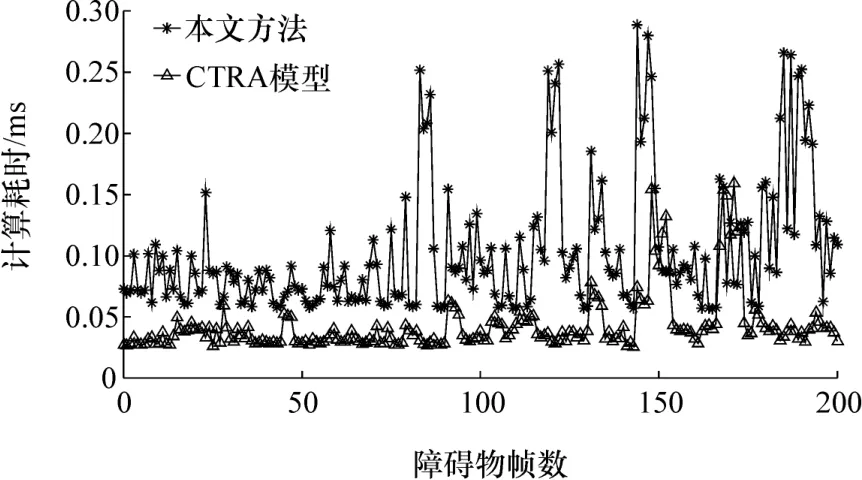
图7 两种方法计算时间对比

提出了一种车辆轨迹预测的方法。该方法首先接收感知得到的障碍物信息，结合高精度地图提供的车道线信息，识别车辆行为，然后建立s-l坐标系，并结合行为识别结果，沿车道横向与车道纵向建立两个多项式方程，分别预测车辆的横向和纵向的运动；再以车道线曲率为约束条件，筛选出一条最优的预测轨迹。最后通过城市环境下的实车实验验证了本文算法的有效性、准确性和实时性，实验结果表明本文所提方法能够较为准确地预测运动车辆未来4 s内的轨迹，预测轨迹合理，处理过程平均耗时仅为0.103 ms。

本研究目前适用于结构化道路环境下运动车辆的轨迹预测，同时认为车辆遵守交通规则且只做匀速或匀变速运动，下一步将着重解决环境车辆做变速运动时的轨迹预测问题。