分段光滑碰撞振动系统吸引域结构变化机理研究

张 惠， 丁旺才， 李险峰

(1. 兰州交通大学 机电工程学院，兰州 730070；2. 兰州交通大学 数理学院，兰州 730070)

含间隙和预紧弹簧的碰撞振动系统在齿轮齿条间隙调整机构[1]、含作动器的隔振系统[2-3]及超磁致伸缩激振器[4]等机械系统中广泛存在，通过螺栓调节弹簧压缩量来调节预紧力大小，预紧弹簧的存在使系统的非光滑程度增加，系统流形的光滑度为2[5]。碰撞振动系统的全局分析主要是为了获得系统的渐近或稳态响应。对于相空间中存在多个吸引子的情况，如果随机选择初始条件，除非知道各个吸引子的吸引域，否则一般情况下不能确切的了解其渐近响应。此外，在碰振系统中即使当参数发生微小的变化，也可能会导致相空间结构的巨大的变化，比如吸引集的突然出现或消失或者稳定性发生改变，所以需要理解哪些参数及如何导致这些拓扑结构的变换或者分岔的产生。全局分析在科学和工程领域，如研究转子轴承、齿轮等机械系统、随机系统全局分析和分岔、气动弹性系统周期的、混沌的颤振的运动、控制系统的鲁棒性等方面具有重要应用[6-8]。

对于全局分析的理论解析方法方面，比较著名的是Melnikov方法[9-10]。此外Parker等[11]叙述了吸引域的概念并呈现了一些动力系统中吸引域、轨道边界即分界线的例子，并提出了计算和绘制吸引域边界的方法。Komuro等[12]从同宿、异宿及周期轨道等方面深入分析了双涡卷电路的全局两参数分岔结构。Jiang[13]研究了转子系统这一含接触的分段光滑动力系统的全局响应特性。Zhang等[14]推导了一类碰撞振动拟哈密顿系统的全局次谐Melnikov函数。

由于非线性系统的类型多、求解难度大，目前没有统一的解析求解方法，所以数值方法一直是非线性动力系统全局分析的可靠选择和研究重点。由于逐点数值直接积分法需要花费很长的时间才能得到系统中存在的吸引子及其吸引域，这常使人们无法忍受，所以Hsu[15-19]提出更高效的胞映射法。Hong等[20-22]等借助于广义胞映射图论方法发现了嵌入在分形吸引域边界内的混沌鞍，混沌鞍碰撞混沌吸引子导致混沌吸引子完全突然消失，产生混沌的边界激变。冯进钤等[23]基于图胞映射理论，提出了一种擦边流形的数值逼近方法，研究了典型Duffing碰撞振动系统中擦边诱导激变的全局动力学。Grebogi等[24-26]研究了吸引域边界的质变，即吸引域边界性质的改变。Nusse等[27]将吸引域的边界点按各自的特点分成了四类，并提出了域拥有域胞及域胞产生和摧毁的充要条件。洪灵等[28]证明Wada域边界上的混沌鞍导致局部鞍结分岔具有全局不确定性结局。张永祥[29]对典型混杂系统吸引域及边界的理论描述、流形分析及吸引域算法进行了研究。韩清振等[30]应用分岔图研究了相对转动系统随平方非线性刚度系数及激励角频率变化的全局动力学行为。Hu[31]用平均法研究了含预紧的对称弹性装置的主共振和稳定性，解析得到了稳定和不稳定参数区域。乐源等[32]研究了一类三自由度碰撞振动系统的激变和阵发性。Gritli等[33]认为两足机器人通过斜坡时的两足混沌运动的产生和消除是通过边界激变方式而产生的。赵建学等[34]采用不同控制方法使系统迁移至目标轨道，实现系统吸引子迁移控制。

本文针对机械系统中常见的含间隙和预紧弹簧分段光滑碰撞振动系统，建立了其动力学模型，分别在不同截面上建立了系统的Poincaré映射；研究了随关键参数—激振频率ω变化时系统中共存的各个分支及其发生分岔的过程，利用Lyapunov维数分析了系统的稳定性；分析系统共存分支出现及泯灭的原因；利用Poincaré胞映射法在不同Poincaré截面上研究系统共存吸引子及其吸引域；分析由不同类型的鞍结分支引起吸引域结构发生质变的机理。通过研究系统的吸引子共存及其吸引域结构变化以期为系统的结构优化及控制提供理论支持。

1 系统描述及其运动方程

1.1 力学模型

建立含间隙及预紧弹簧的分段光滑碰撞振动系统模型，如图1所示。左边是激振器中质量为M的力输出杆，其由刚度为K1的线性弹簧和阻尼系数为R1的线性阻尼器连接于支承， 并受到简谐激励Fmcos(ΩT+τ)的作用(Fm为简谐激励力幅值，ω为简谐激励力频率，τ为初始相位)。右边是一个带有预压缩弹簧K2和阻尼系数为R2的平面(无质量)，用来缓冲碰撞。取物块静平衡位置为坐标原点，弹簧K2被预压缩来缓冲振动，设弹簧K2的预压缩量为D。

图1 模型图Fig.1 Model diagram

当X<Δ时，这是一个简单的谐波振子，方程为

(1)

当X>Δ时， 物快与右边预紧弹簧发生接触，因为在接触表面没有质量，方程为

(2)

取无量纲量

则系统的无量纲运动微分方程为

(3)

1.2 方程的解

物块与墙面发生接触阶段(即x≥δ时)，由初始条件

(4)

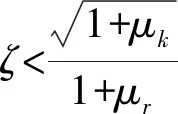
(5)

(6)

其中，

η=ζ(1+μr),

b2=(y0+ηa2+A2ωsinτ0-B2ωcosτ0)/ωd2。

Risk assessment of mountain torrent disaster in small watershed of east Yunnan province SU Wen-hao GAN Shu CHEN Ming-yi(28)

物块与预紧弹簧没有发生接触阶段，由初始条件

(7)

当ζ<1时，式(3)的通解为

(8)

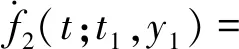
(9)

其中，

2 系统共存吸引子及其吸引域

2.1 系统共存吸引子产生及湮灭分析

图2 随ω变化时系统中共存的各个吸引子Fig.2 Theco-existing attractors in the system as changes with ω

随着激励频率ω的递增，系统稳定的q=2/2周期运动经周期倍化分岔序列，通过PD1，PD2(Periodic Doubling)等分岔点后进入q=4/4,q=8/8、混沌等运动状态，在ω7=2.493 5附近系统经边界激变BC(Boundary Crises)，从混沌运动中退化出稳定的q=2/3周期运动。从图2(b)可以了解到当系统处于混沌运动状态时Lyapunov维数为分数形式。我们再随励频率ω的递减来分析系统中共存的另一分支—A2的运动转迁过程。随着ω的减小，q=2/3周期运动在ω3=2.475附近经历“擦边”分岔GB1(Grazing Bifurcation)，从q=2/3周期运动转迁为q=7/9周期运动，碰撞数in和周期数en如图2(c)和图2(d)所示。随着ω的进一步减小，q=7/9运动经由周期倍化分岔进入q=14/18运动状态。在ω1=2.463附近，q=14/18运动经历第二次“擦边”分岔GB2，擦边后系统共存吸引子也随即消失，只保留稳定的q=2/2周期运动。

2.2 系统共存吸引子吸引域演变规律分析

图3 ω1=2.463，q=2/2和q=14/18吸引子共存Fig.3 ω1=2.463, q=2/2 and q=14/18 attractors coexist

图4 ω2=2.473 6，q=2/2和q=7/9吸引子共存Fig.4 ω2=2.473 6, q=2/2 and q=7/9 attractors coexist

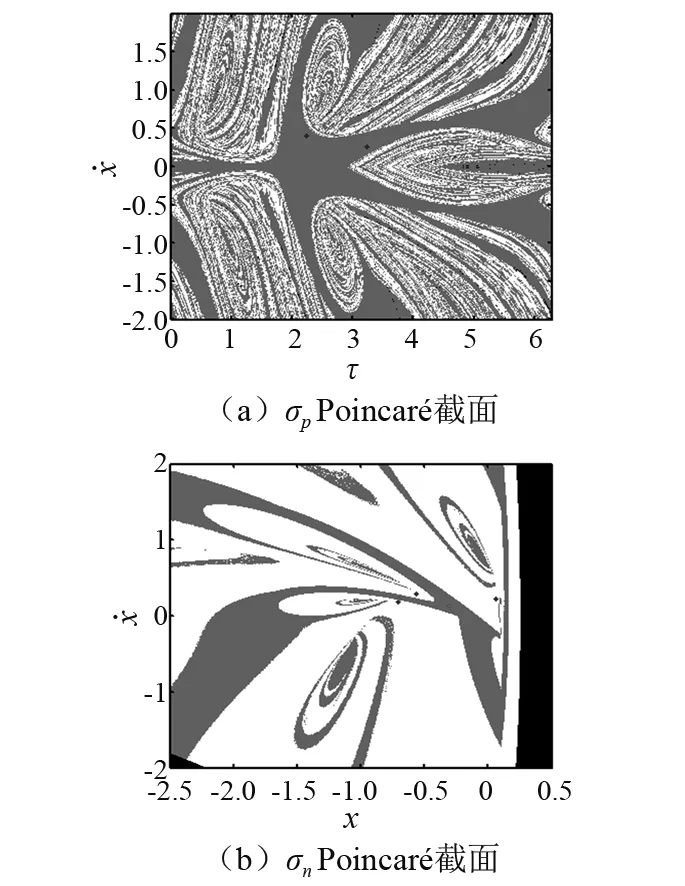
图5 ω3=2.475，q=2/2和q=2/3吸引子共存Fig.5 ω3=2.475, q=2/2 and q=2/3 attractors coexist

图6 ω5=2.48, q=4/4和q=2/3吸引子共存Fig.6 ω5=2.48, q=4/4 and q=2/3 attractors coexist

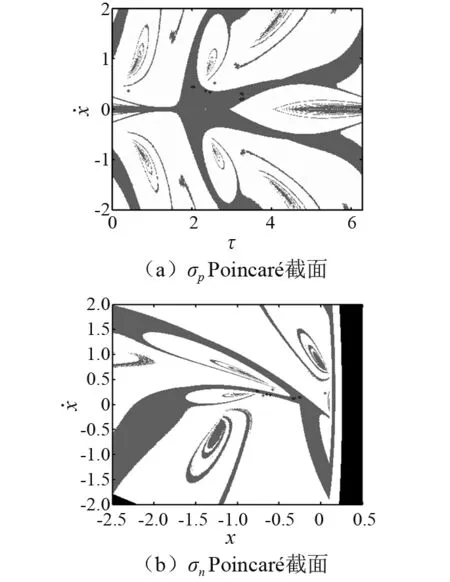
图7 ω6=2.486，q=8/8和q=2/3吸引子共存Fig.7 ω6=2.486, q=8/8 and q=2/3 attractors coexist

图8 ω7=2.493 5，混沌吸引子和q=2/3吸引子共存Fig.8 ω7=2.493 5, chaos and q=2/3 attractors coexist

3 非光滑系统吸引域结构变化机理研究

3.1 由“擦边”运动诱导出现的平常型鞍点分支

从图3～图8中可以了解到：A1分支(即主分支)虽然经历了倍周期分岔，但在倍化分岔序列参数范围内，各个吸引子的吸引域在σp和σnPoincaré截面上均没有发生太大的变化。但是随着ω的减小，从图5(a)～图8(a)可以观察到，在ω∈[2.475,2.48]之间的某个临界参数值处，A2分支中的q=2/3周期运动的吸引域边界在σpPoincaré截面上发生了分形，发生了光滑—分形质变。利用二分法逼近临界质变点，得到临界质变发生在ω=2.475 52附近。分析得到：A2分支的吸引域之所以发生了结构质变，是因为此时系统的状态空间中出现了一个由擦边运动所诱导的鞍结分岔所形成的新分支—A3分支，如图10所示。其起始于q=5/6周期运动，分为5片，每一片随着ω的减小均通过周期倍化分岔很快的进入混沌，所以A3分支只存在于ω∈[2.475 15,2.475 5]这样很小的一段参数范围内。在σp和σnPoincaré截面上的吸引子和吸引域如图9(a)和图9(b)所示。这一分支的出现使q=2/3周期运动的吸引域在这一邻域既发生了边界质变，即吸引域从光滑变为了分形结构，也发生了内部激变，即n(n=2,3,…)片混沌吸引子与其吸引域边界发生相切，这两种类型的全局分岔。q=5/6周期运动在σpPoincaré截面上的五个周期点坐标如表1中SN1各值所示。各个周期点处系统Jacobian的特征值如表2所示，其中Si(i=1,3,4,5)的特征值0<ρ1<1<ρ2，其为平常型鞍点[35]。A3分支的出现使系统在ω=2.475 52时状态空间中存在三个不同的吸引子，即q=2/3,q=4/4和q=5/6。同时因为吸引域的分形结构，使一些吸引子可能不在它们自己的吸引域内，这个特性是不同于光滑系统的吸引域属性。所以ω=2.475 52时由于鞍结分岔导致了系统吸引域结构的变化。随后，随着ω的减小A3分支经历周期倍化分岔进入混沌，在ω=2.475 14时系统运动轨道与碰撞边界相切，发生擦边分叉，A3分支消失。

图9 ω=2.475 52,q=2/3,q=4/4,q=5/6吸引子共存Fig.9 ω=2.475 52,q=2/3,q=4/4 and q=5/6 attractors coexist

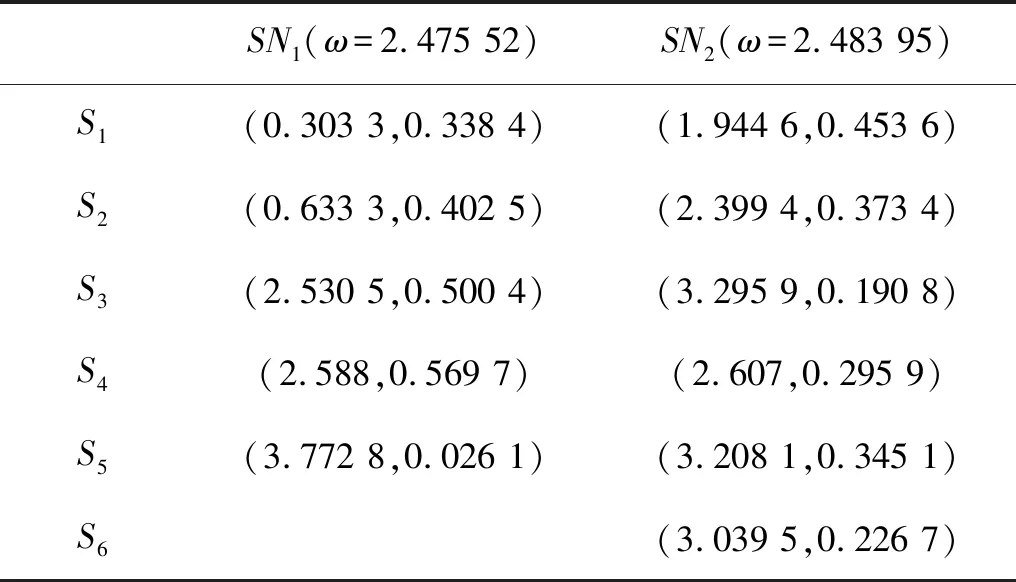
SN1(ω=2.475 52)SN2(ω=2.483 95)S1(0.303 3,0.338 4)(1.944 6,0.453 6)S2(0.633 3,0.402 5)(2.399 4,0.373 4)S3(2.530 5,0.500 4)(3.295 9,0.190 8)S4(2.588,0.569 7)(2.607,0.295 9)S5(3.772 8,0.026 1)(3.208 1,0.345 1)S6(3.039 5,0.226 7)

表2 SN1各点处Jacobian矩阵特征值

图10 随参数ω变化时系统共存的吸引子Fig.10 The coexists attractors in the system as the parameter ω changes

3.2 由周期倍化分岔诱导出现的翻转型鞍点分支

通过进一步研究还发现：在ω=2.483 95时，系统状态空间中又出现了一个新的分支—A4分支。A4分支的出现是由于系统中的周期倍化分岔所诱导的鞍结分岔所形成，随着ω的增加，其起始于q=6/6周期运动。在σpPoincaré截面上的六个周期点坐标如表1中SN2各值所示。各个周期点处系统Jacobian的特征值如表3所示，其中Si(i=1,2)的特征值ρ1<-1<ρ2<0，其为翻转型鞍点。A4分支的出现也使A1分支的吸引域经历了光滑—分形质变。当ω=2.483 95时，在σp和σnPoincaré截面上的吸引子和吸引域如图11(a)和图11(b)所示。其后随着ω的增加，A4分支经历周期倍化分岔进入混沌，在ω=2.484 68时混沌吸引子与其吸引域边界发生内部边界碰撞，造成A4分支的消失。

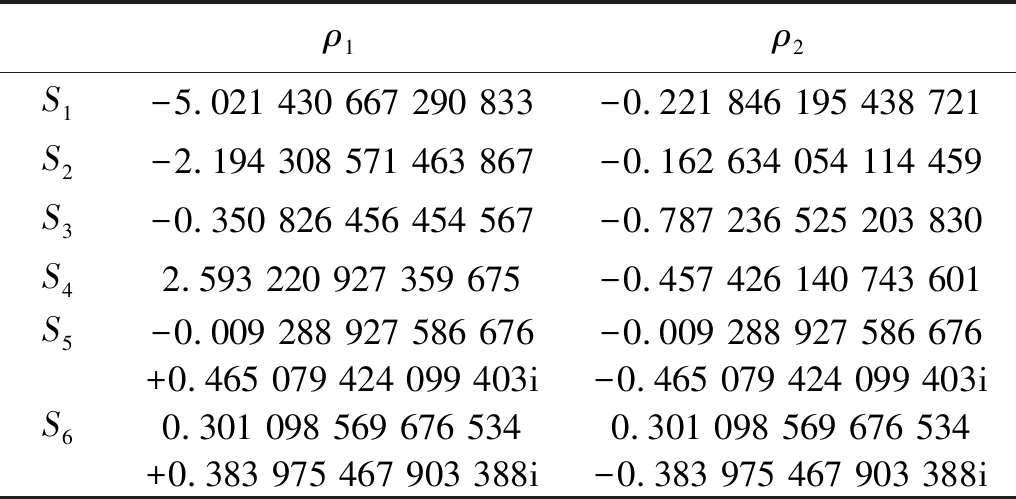
表3 SN2各点处Jacobian矩阵特征值

图11 ω=2.483 95,q=2/2,q=4/4,q=6/6吸引子共存Fig.11 ω=2.483 95,q=2/2,q=4/4 and q=6/6 attractors coexist

而且当随着系统其他主要分岔参数变化时(比如间隙δ)，引起系统共存吸引子的产生及泯灭的原因是相同的，引起系统吸引子吸引域发生质变的机理也是相同的，此处不再赘述，所以上述关于吸引域质变机理的研究具有普适性。

4 结 论

本文建立了一类单自由度含间隙和预紧弹簧的分段光滑碰撞振动系统模型，建立了系统的Poincaré映射；研究了系统随关键分岔参数ω变化时系统吸引子共存情况，利用Lyapunov维数分析了系统的稳定性。通过不同平面上的的Poincaré映射，来研究系统的碰撞和周期运动；利用改进的胞映射法，研究了系统中共存吸引子的吸引域。研究了由内部边界碰撞和非光滑相切引起的混沌吸引子的产生和摧毁过程，重点分析了吸引域结构变化情况。得出如下结论：

(1) 非光滑系统中吸引子可由两种情况所诱导产生——擦边分岔二是周期倍化分岔所诱导。

(2) 非光滑系统中吸引子的消失是由两种情况所形成：一是系统运动轨道与碰撞面相切，即由外部边界碰撞所引起的擦边分岔所形成；二是由于由周期倍化分支所形成的混沌吸引子与其吸引域边界碰撞即发生内部边界激变所形成。

(3) 非光滑系统中吸引域发生光滑—分形质变是由于系统由擦边分岔所诱导出现的平常型鞍点，及由周期倍化分岔所诱导的翻转型鞍点的稳定与不稳定流形发生横截相交，从而造成吸引域分形结构的出现。