一种海洋MEMS电导率传感器结构优化设计*

李志伟,李红志,贾文娟,李醒飞*

(1.天津大学精密测试技术及仪器国家重点实验室,天津 300027;2.国家海洋技术中心,天津 300112)

电导率传感器是用来测量海洋电导率参数的重要仪器,四电极式电导率传感器[1-2]本身体积较小且多为开放式结构,易于清洗和防止海水中微生物附着。此外,此类传感器在测量时还具有低流体阻力[3],低热量,低功耗等优点。伴随着对于海洋观测需求的提升,MEMS技术开始逐渐应用到海洋观测仪器领域[4]。基于该项技术的传感器体积大大减小,能够测量小空间范围海水的电导率,降低了海洋观测仪器的生产制造成本,为电导率传感器在海洋中的大规模布放和应用提供了基础。

目前,国外主要有美国伊利诺伊大学的Dongming He[5]等人加工出了电极宽度低至0.1 mm的条形MEMS四电极电导率传感器。丹麦科技大学的Hyldgard等人[6-7]基于硅材料的MEMS技术开发了一种安装于鱼体内的条形MEMS四电极电导率传感器,具有较高灵敏度和快速响应的特性。南佛罗里达大学的Heather等人[8-11]研究出基于MEMS技术并使用了液晶聚合物(LCP)材料制作的环形MEMS四电极电导率传感器。印度的Jijesh J J[12]等人开发出一套CTD测量系统并在其中使用了条形MEMS四电极电导率传感器。国内主要有浙江大学张高燕等人[13]采用等离子磁控溅射设备研制了MEMS分离式环形四电极结构。河海大学刘海韵等人[14-15]和广州中科院先进技术研究所陈秋兰[16-17]等人则分别发表了关于MEMS四电极电导率传感器的加工工艺与结构设计的相关专利。

由于电场分布范围更小,MEMS四电极电导率传感器的环形结构较条形更优[18],具有良好的应用前景。其中文献[9]中环形结构传感器电导率测量准确度为±1.47%,文献[10]中相同结构的传感器灵敏度最高为1.2 cm-1。本文从传感器基本结构与测量原理出发,采用电场基本理论分析影响传感器测量准确度和灵敏度的因素,进而通过优化结构设计来提高传感器整体性能。

1 环形四电极电导率传感器测量原理

海水电导率范围通常在5 mS/cm～70 mS/cm,使用式(1)来计算:

σ=KI/V

(1)

式中:σ为被测海水电导率,K为电导率传感器的电导池常数,I为激励电流,V为两测量电极间的电压值。文献[9-10]环型四电极电导池结构如图1所示,在厚为1 mm的10 mm×10 mm玻璃基底上一个圆形平面电极和三个环形平面电极组成且同心等距排列,电极厚度约为几百纳米。由中心向外分别为第一电极和第二、三、四电极,第一电极半径为2 mm,第二,三,四电极宽度为0.25 mm,间距为0.75 mm。第一电极和第四电极称为激励电极(电流电极),第二电极和第三电极称为测量电极(电压电极)。

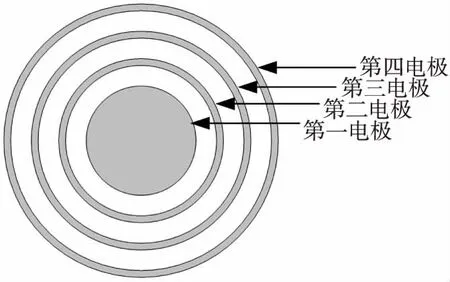
图1 优化前环形四电极电导池结构

当电导池浸泡在海水溶液时,通过对第一电极和第四电极通入一定频率范围的交流电流信号,在电极间会产生一个稳定的电场,电势由第一电极到第四电极递减,测量两个测量电极间的电势差,然后根据电流值计算出电导率值。如果第二电极和第三电极能分别更靠近于第一电极和第四电极,即加大第二电极和第三电极之间的间距,则会在两个测量电极之间得到比原有更高的电势差,获取的海水阻值和阻值变化范围就越大,所测海水电导率的偏差就会越小,灵敏度越高。在整体电导池尺寸确定的情况下,这同时取决于其他两个电极的尺寸大小。同时处于最高电势处第一电极的极化效应[19]的影响也不能忽略,需要具体进行分析。

2 电导池电场分析与结构优化设计

(2)

式中S为电流流经电极的面积矢量,由于J为矢量,所以在切向和法向上分别可以进行分解,如图2所示。电流流经电极和海水,电导率分别为σ2和σ1,根据电流密度的边界条件有an·(J1-J2)=0,J1和J2分别为海水一侧和电极一侧的电流密度矢量。

图2 在海水和电极分界面的电流密度分量

根据电流密度在两种介质上法向分量上连续,可知电流密度在海水与电极上的法向分量满足:

Jn1=Jn2

(3)

且电流密度J和电场强度E有如下关系:

J=σE

(4)

由于电场的切向分量在分界面上是连续的,所以有:

Et1=Et2

(5)

由式(4)-(5)得出海水和电极电流密度的切向分量满足:

(6)

即海水和电极分界面上电流密度的切向分量之比等于电导率之比,进而由式(3)和(6)有:

(7)

由于σ2≫σ1,由式(7)可知θ1是一个非常小的角,则易知海水中电流密度的切向分量很小可以忽略不计,所以海水电流密度值可以看作是其法向分量的值。由式(3)和(4)得:

En2σ2=En1σ1

(8)

在电极与海水的分界面处的电荷密度ρs可以由下式算出:

ρs=Dn1-Dn2

(9)

式中Dn1和Dn2分别是海水和电极中法向电通量密度。且电极和海水在边界处满足本构方程:

D=εE=ε0εrE

(10)

式中:ε为介质的电介质常数,εr为介质的相对电介质常数,ε0=8.85×10-12/(F/m)为真空电容率。将电荷密度转化为与电流密度的关系,由式(4)和式(8)～式(10)得:

(11)

由于电导池电场由电荷产生电场分量的矢量叠加,分析较为复杂,且由于趋肤效应的存在,电极表面上的电荷主要分布在电极边缘处的薄圆环区域内,如图3。不难得知电极表面电荷产生电场由电极表面向外递减,并中轴线处电场范围达到最远。所以可直接分析在中轴线上与第一电极表面距离为z的某点P的电场强度。

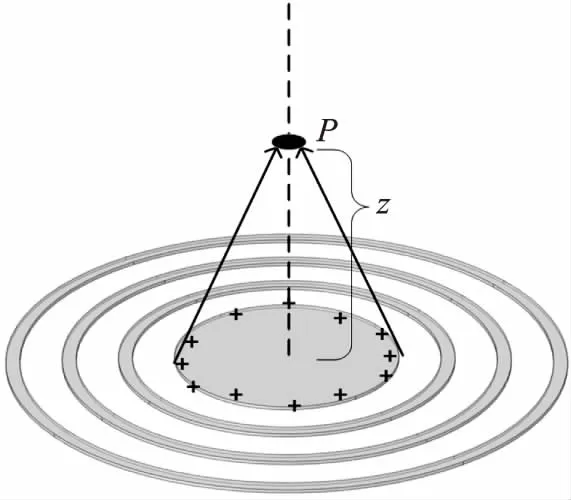
图3 电极在P点产生的电场示意图

第一电极在中轴线P点的电场强度可用下列公式计算:

(12)

a为电荷在第一电极边缘处薄圆环的内径,b为电荷在第一电极聚集区域薄圆环的外径,有a≈b。在z不变的情况下,第一电极半径越大,则在P点处的电场强度越小,相应电导池电场在海水分布范围就越小。将式(11)代入到式(12)中得到式(13):

(13)

图4 半径为0.5 mm,1.0 mm,1.5 mm,2.0 mm的第一电极边界到电导池边界的距离

以第一电极半径为变量,将P点电场强度和第一电极边界到电导池边界的边界距离进行绘制,如图5。

图5 P点电场强度和第一电极到电导池边界距离随第一电极半径变化图

由图5可以看出随着第一电极半径的变大,P点电场强度Ep和d都在减小,我们希望Ep尽可能小,d尽可能大。由图得出在第一电极半径为1 mm时,d与Ep的差值最大,即为该电极的最佳尺寸。为了保证两个测量电极间的间距尽量大且合理,将两个测量电极宽度设置为中心电极的1/4,第四电极在第一电极半径的1/2,所以分别取两个测量电极的宽度为0.25 mm,第四电极宽度取0.5 mm,电极厚度为100 nm。优化后的尺寸结构图如图6所示。

图6 优化后的尺寸结构图

3 电导池仿真

3.1 电导池电场和电势仿真

仿真中尺寸和材料参数见表1。

表1 优化后电极,基底以及海水的几何尺寸参数

根据参数设置得到电导池的模型如图7所示。

图7 电导池在海水半球中的模型

对电导池模型的2个激励电极施加101Hz～1010Hz范围内的交流激励频率,分别在海水电导率为5 mS/cm,10 mS/cm,20 mS/cm,30 mS/cm,40 mS/cm,50 mS/cm,60 mS/cm,70 mS/cm得到P点的电场强度Ep如图8所示。

图8中电导率在5 mS/cm～70 mS/cm时,同一电导率下,频率在10 Hz～1 000 kHz范围内对应的P点电场强度不发生变化即电导池电场不变,进而由前面分析得电极间电势不变。选取频率=10 kHz,电导率=40 mS/cm时对应的电导池电势分布和以电导池为中心的电势曲线如图9所示。

图8 P点电场强度随频率和电导率变化示意图

图9 频率=10 kHz,电导率=40 mS/cm时电导池电势分布和曲线图

由图9可知电导池电势由中心向外扩散,并均匀分布且由中心向外经过两个测量电极的电势差较大,保证了后面能够测得较高的海水阻值并提高电导率测量的准确度。

3.2 电导池电路与测量结果

电导池在实际测量中会发生复杂的化学反应,除了前面提到的极化效应,主要还有电容效应[21],以及由此产生的双层电容Cdl(与电极表面积有关),双层电容主要由电极材料和电解质溶液的离子浓度决定,可以由下式算出:

Cdl=cdlA

(14)

式中:cdl代表单位面积双层电容,在40 μF/cm2[22]左右,A为测量电极的表面积。根据计算分别得到第一,二,三,四电极的双层电容Cdl1=1319.16 nF,Cdl2=864.16 nF,Cdl3=2 593.48 nF,Cdl4=5 970.4 nF。另外还有导线产生的寄生电容Cp(一般在100 pF左右)的阻抗和电极在海水中与其他物质发生化学反应产生的法拉第电阻Re[23](一般为50 kΩ),由于电导池为环形对称结构,取其中一侧的等效测量电路如图10所示。

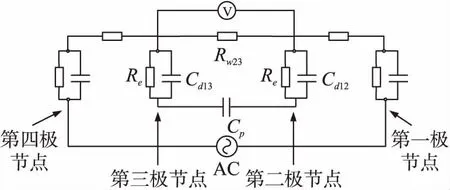
图10 电导池等效测量电路

RW23为第二电极和第三电极之间测得的海水电阻。实际中所测量的海水阻抗值Z为:

(15)

式中:α为双层电容的理想系数约等于1,ω为激励信号角频率且有ω=2πf。在激励频率范围为10 Hz～1 000 kHz对模型施加交流激励信号,在海水电导率分别为5 mS/cm,10 mS/cm,20 mS/cm,30 mS/cm,40 mS/cm,50 mS/cm,60 mS/cm,70 mS/cm时得出优化前后电导池结构测量电极间的海水阻抗与频率的对应关系,如图11所示。

图11 优化前后结构海水测量阻抗值-频率图

由图11可以看出,随着频率变大,各海水电导率曲线对应阻值开始变小然后分别进入一段平衡后又开始下降。这是因为低电导率海水阻值高,所以低电导率的海水曲线比高电导率的海水先进入平衡。高电导率海水阻值低,所以高电导率海水曲线比较低电导率的海水延后下降。各曲线同时平衡时对应的频率范围为最终测量时的激励频率范围即10 kHz～100 kHz,如图中方框所示。方框左侧在10 Hz～10 kHz范围内,由式(15)知,频率较小时,水体阻抗值Z主要由双层电容Cdl2,Cdl3和等效海水水体电阻RW23共同决定,随着激励频率变大,Cdl2和Cdl3的容抗值迅速减小导致阻抗值Z快速减小。频率在100 kHz以上方框右侧时,高频使得交流电流几乎只通过Cp,所以Z值主要由Cp容抗值决定。当频率在10 kHz～100 kHz的范围内,电容Cdl2,Cdl3,Cp的容抗值远小于海水阻值RW23,阻抗值Z基本不随频率发生变化即为所测海水阻值RW23。这一频率和电导率范围内,优化前的结构对应的海水测量阻值变化为50.79 Ω～710.60 Ω之间,优化后的结构对应的水体阻值变化为222.96 Ω～3121.09 Ω之间,水体阻值以及变化范围的大小会影响海水电导率测量准确度的高低,水体阻值及其变化范围越大,则电导率测量的准确度越高,优化后的结构相比优化前的结构对应相同电导率测量的水体阻值提高4.39倍,同时对应水体阻值测量范围也提高4.39倍。

4 优化前后传感器灵敏度与准确度分析

本文中此类型传感器灵敏度主要由电导池常数K表示,K值越大则表示传感器的灵敏度越高,相同电导率变化能够引起测量阻值变化较大。通常K都是通过式(16)得出:

(16)

L为两测量电极之间的距离,S为两测量电极的正对面积。但是由于本文中所分析的电导池结构为环形结构,属于异型电导池结构,所以需要使用模型进行计算。即在图11中激励频率为10 kHz和100 kHz时,8个电导率点对应水体阻值和海水电导率σ1的乘积即得出电导池常数K:

K=RW23·σ1

(17)

计算所得传感器优化前后导池常数见表2和表3。

表2 优化前电导池常数计算表

表3 优化后电导池常数计算表

由表2和表3对比后可知,优化前后的结构在10 kHz～100 kHz之间各电导率点对应的电导池常数分别基本稳定在3.6 cm-1和15.6 cm-1,传感器结构优化后比优化前灵敏度大约提高了4.3倍。

针对两种结构,同时在10 kHz和100 kHz之间分别取20 kHz,40 kHz,60 kHz,80 kHz四个频率点对应的水体阻抗值和各自电导池常数代入到式(17),反算出结构优化前后在这几个频率点对应的电导率值与前面设定的8个电导率值的偏差,如表4和表5。

由表4和表5不难看出,优化后的结构普遍比优化前的结构电导率测量偏差提升了一个数量级,即优化前电导率测量偏差基本在0.1数量级,而优化后电导率测量偏差基本在0.01数量级,优化后的结构测量偏差减小显著。然后用优化前后各自偏差与电导率真实值相比来表示准确度,进一步将优化前后传感器结构仿真的准确度与灵敏度与相关文献同类结构进行对比,如表6。

由表6可知,优化前结构的仿真结果的准确度和灵敏度分别与文献[9-10]指标接近,仿真结果可靠,且优化后的结构在准确度和灵敏度都有不同程度的提升,表现出较好的性能。

表4 结构优化前四个频率点电导率偏差

表5 结构优化后四个频率点电导率偏差

表6 准确度与灵敏度对比

5 结论

本文针对一种MEMS四电极电导率传感器结构进行了分析,利用电场基本理论分析优化了传感器结构,使用COMSOL对优化前后传感器结构的进行仿真验证。最后得到在海水电导率范围为5 mS/cm～70 mS/cm,激励频率范围为10 Hz～100 kHz时,优化后结构比优化前阻值测量范围扩大4.39倍,优化后的结构准确度提高至±1.18%,灵敏度提高至15.6 cm-1,表现出更好的传感器测量性能。