基于蚁群算法的超声波水体悬移质浓度测量研究*

张述仁,徐 雅,谢代梁,徐志鹏,刘铁军,王月兵

(中国计量大学,浙江省流量计量技术研究重点实验室,杭州 310018)

水体悬移质含量测量在水利、海洋、生态系统等领域占据着重要的位置,悬移质的分布、扩散、沉降等影响着港口、航道和生态环境,因此,水体悬移质浓度和粒径等参数的测量对水利建设、环境保护和水土流失等具有重大意义[1-2]。

超声波测量法因其具有声波穿透性强、探测频带宽、对被测流体无影响且易实现在线检测等特点[3-4]近年来在水体悬移质含量测量研究方面获得了广泛关注[5-6]。研究表明,在超声衰减法测量悬移质参数的反问题求解中,反演算法至关重要,目前应用较多的反演算法主要有Twomey算法、Chahine算法[7]、BFGS(Broyden-Fletcher-Goldfarb-Shanno)、DFP(Davidon-Fletcher-Powell)、遗传算法(Genetic Algorithm)[8]等,不同情况下,上述算法有自己的优势和局限性,如BFGS和DFP算法属于局部最优算法,求解时容易陷入局部最优而偏离真值,遗传算法具有全局收敛性,但搜索收敛时间较长,不满足实时测量需求。

蚁群算法ACA(Ant Colony Algorithm)是由意大利学者Dorigo M等提出的一种群体智能仿生算法,因其鲁棒性强、有自组织性、并行分布式计算、易于与其他方法相结合等特点[9],在网络路由[10]、函数优化[11]、路径分配[12]、智能导航[13]以及超声波检测[14]等很多领域中各类优化问题上得到了广泛应用,并取得了显著的应用成果。本文结合超声衰减实验研究了蚁群算法在超声衰减法测量水体悬移质浓度中的应用,着重针对蚁群算法中的关键参数—蚂蚁总数、蚂蚁最大移动次数、信息素挥发系数和转移概率进行了优化研究。

1 超声衰减法测量原理

1.1 超声衰减

超声波在悬移质溶液中传播时根据悬移质颗粒的大小、浓度等的不同会产生不同角度的反射和折射,宏观上体现为经过介质的超声波的能量的衰减[15]。在大多数测量情况中,引起衰减的主要损失机制包括吸收、散射、粘性耗散和热耗散。衰减系数是超声衰减法中主要的测量参数,总衰减系数理论上可表示为各种声衰减系数的叠加总和。

超声波在悬移质溶液中经过多次反射,在接收换能器端会形成多次回波,衰减损失逐渐变大表现为电压幅值逐级递减。超声衰减理论过程如图1所示。

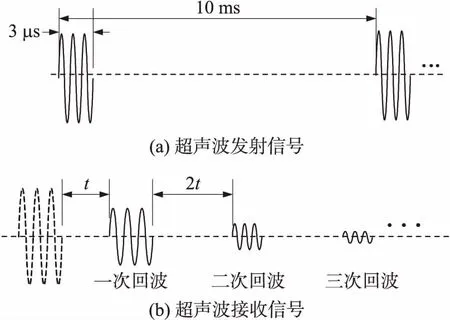
图1 超声波衰减理论过程

实际的声衰减系数α受到温度、悬移质对超声波的吸收性质、悬移质浓度、粒径、质量以及形状等诸多方面的影响,在实验过程中,通过接收探头接收到的电信号幅值与超声波传播的距离来简便计算衰减系数,计算公式[15]如式(1)所示:

(1)

式中:αw为超声波在水中的衰减系数;A0为加入悬移质后形成悬浊液所测的电压幅值;A1为未加入悬移质时清水中所测的电压幅值;L为声距。

1.2 测量模型

ECAH(Epstein Carhart Allegra Hawley)模型是Epstein等学者从微体积元的质量、动量和能量守恒定律出发,建立的能精确描述球形颗粒两相离散系中声波动行为的模型[16-17],也是超声波在两相流中传播的经典模型,在该模型条件下可得到悬移质颗粒两相流复波数方程[6]如式(2)所示:

(2)

式中:kc为连续介质中的波数;κ为悬浊液中的复波数;φ为悬移质溶液体积浓度;R为悬移质颗粒半径;An为n阶压缩波散射系数。

式中:复波数κ由式(3)给出;

(3)

式中:ω为角频率,s-1;cs为超声波在液固混合物中的传播声速,m/s;αs为超声波在悬移质溶液中所对应的衰减系数;

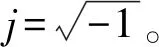
由式(2)、式(3)可推导得到衰减系数的计算表达式[18]如式(4)所示;

(4)

1.3 测量系统

超声水体悬移质实验系统如图2所示,由超声换能器发射端将电能转化为声能,超声波在悬浊液中传播时发生衰减,超声换能器接收端将接收到的衰减超声信号转换为电信号,再利用数据采集装置将接收到的电信号进行采集,经过滤波去噪和频谱分析,最终计算获得实验超声衰减系数,装置实物及主要参数如图3、表1所示。

对水体悬移质颗粒两相流的浓度测量,传统人工采样分析的烘干法是精度较高的一种测量方法,因此将实验后的悬移质水样采用烘干法进行分离析出,经过高低温实验箱烘干冷却,再由精密天平称重,并由此计算出悬移质溶液体积浓度,以此作为本次实验结果参考值。

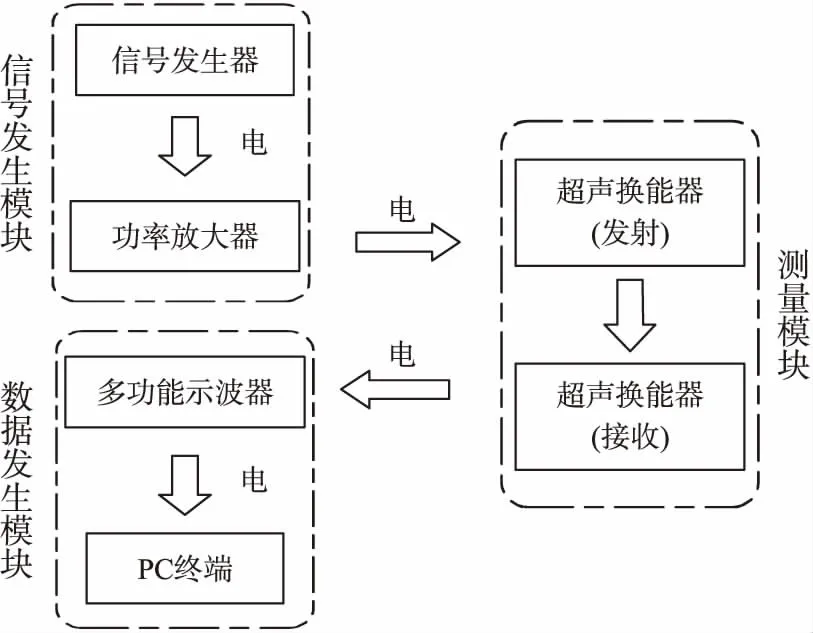
图2 实验系统流程示意图

图3 实验装置实物图

表1 测量系统组成仪器主要参数

2 蚁群算法应用

2.1 目标函数设定

蚁群算法是一种实用性很广的优化算法,把超声衰减法测量中涉及的反演问题看作是优化问题,在优化算法中通过构造目标函数,将悬移质溶液中固相浓度作为寻优量进行寻优,进而得到浓度最优值。应用最小二乘法构造目标(误差)函数[6]如式(5)所示:

(5)

式中:αmeas为实际实验测量中得到的超声衰减谱,由式(1)计算得出。αsim为理论超声衰减谱[6]由式(4)推导得出,可表示为式(6);

αsim=α(f,φ,R,P)

(6)

式中:f,φ,R分别是声频率,悬移质溶液体积浓度和固相颗粒半径,P为包含了各种参数的矢量。

将悬移质浓度作为蚁群寻优目标,结合ECAH模型和浓度、粒径、频率等变量计算理论声衰减谱,根据所得理论衰减系数和实验衰减系数计算出目标函数值。在蚁群算法运行过程中寻找目标函数ERME的最小值,此时蚁群的寻优目标达到最优值,即悬移质溶液浓度φ。

2.2 蚁群算法步骤

蚁群算法程序流程如图4所示,开始程序随机初始化模型参数蚂蚁总数m、蚂蚁最大移动次数times、信息素挥发系数ρ和转移概率p并获得每只蚂蚁的初始位置。然后算法通过不断迭代直到蚂蚁移动次数达到最大值时,输出最优目标函数值和最优解[19]。

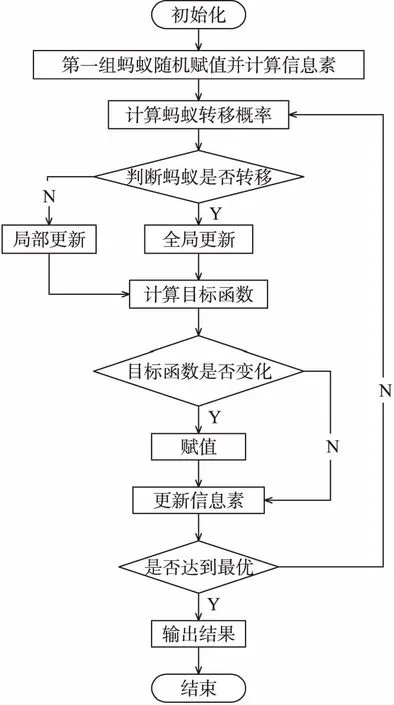
图4 蚁群算法程序图

2.3 蚁群算法最佳参数的确定

蚁群算法中相关参数的设定对算法的性能有很大的影响,针对本次实验,为了使算法的性能达到最佳,对影响算法性能的主要参数(蚂蚁总数、蚂蚁最大移动次数、信息素挥发系数和转移概率)进行了优化计算,采用MATLAB2014编程并通过控制变量法对以上参数进行仿真研究,得到了蚁群算法性能与各参数之间的关系。

图5给出了蚂蚁数量对算法性能的影响。由图可得,蚁群算法中蚂蚁数量m值较小时,算法稳定性和全局搜索能力弱,m值过大时,算法的收敛速度会降低。当蚂蚁数量为20时,目标函数值达到最小且趋于平稳,此时得到全局最优解。

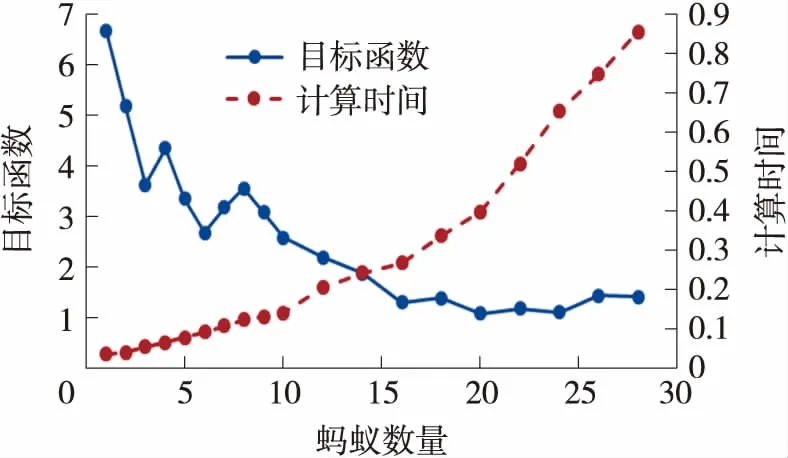
图5 蚂蚁数量与算法性能关系

设置蚂蚁数量为20,通过数值仿真得到蚂蚁移动次数对算法性能的影响如图6所示。由图可得,蚂蚁最大移动次数times取值较大,全局搜索能力强,但收敛速度低,times取值较小,算法稳定性变差。当蚂蚁最大移动次数为140、90时,目标函数值较小,但times=90时目标函数值较小且趋于平稳,此时算法稳定性较好,且收敛时间较短,故times=90为最优选择。

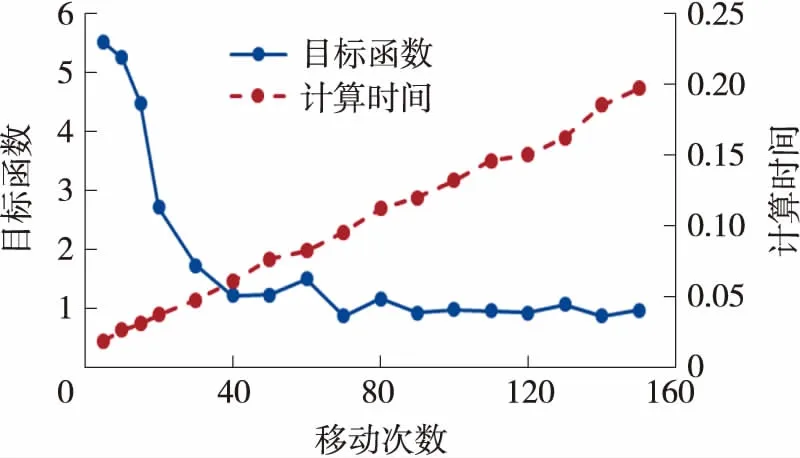
图6 蚂蚁移动次数与算法性能关系

设置蚂蚁数量为20,蚂蚁转移次数为90,为防止信息素无限积累,规定ρ取值范围为[0,1],数值仿真得到信息素挥发系数对算法性能的影响如图7所示。由图可得,信息素挥发系数ρ取值较大时算法收敛性变好,但全局搜索能力变弱,ρ取值较小时收敛性变低。当信息挥发系数为0.2、0.3和0.4时,目标函数值相对较小,全局搜索能力强,信息素挥发系数在0.35～0.70范围内计算时间相对较少,算法收敛速度快,故ρ=0.4为最优选择。

设置蚂蚁数量为20,蚂蚁转移次数为90,信息素挥发系数为0.4,p取值范围为[0,1],数值仿真得到转移概率对算法性能的影响如图8所示。由图可得,转移概率p取值较大时算法收敛性低,全局搜索能力弱,p取值较小时算法全局搜索能力强,收敛性较好。当p=0.6时,目标函数值达到最小,计算时间最短,此时算法全局搜索能力强,收敛性好,且较为稳定,故p=0.6为最优选择。

图7 挥发系数与算法性能关系

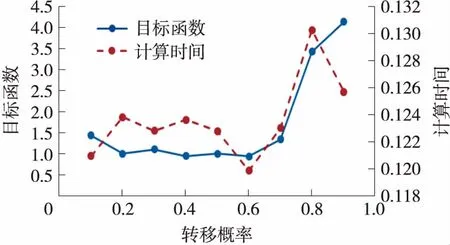
图8 转移概率与算法性能关系

通过图5～图8分析相关参数对算法性能的影响,得到本实验中蚁群算法的主要参数最佳设置如表2所示。

表2 蚁群算法参数组合最佳设置

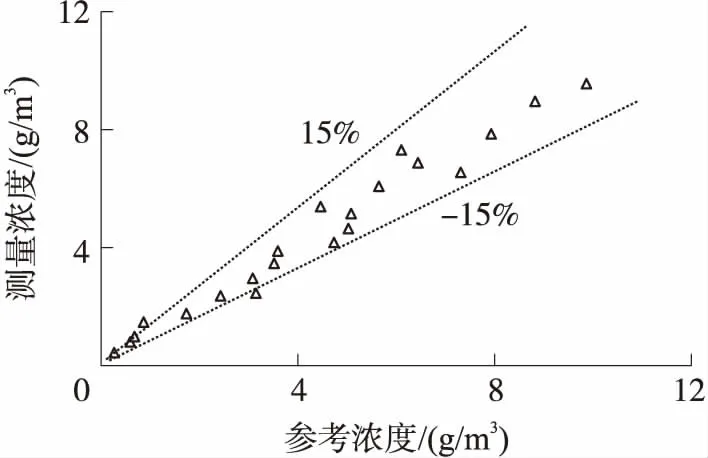
图9 R=0.107 mm测量值与参考值比较图

3 结果分析

对于进行超声衰减实验的三组粒径分别为0.107 mm、0.085 mm、0.062 mm的不同浓度的悬移质水样,由蚁群算法所得的测量浓度值和由烘干法所得参考浓度值如表3所示,图9～图11分别给出了测量浓度值和参考浓度值的对比情况。

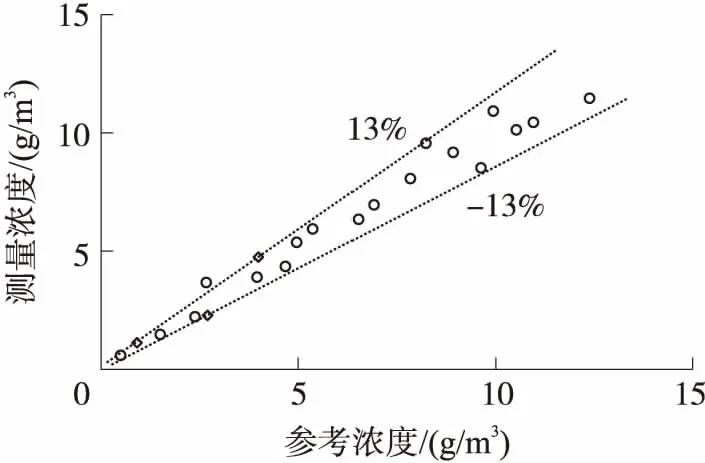
图10 R=0.085 mm测量值与参考值比较图

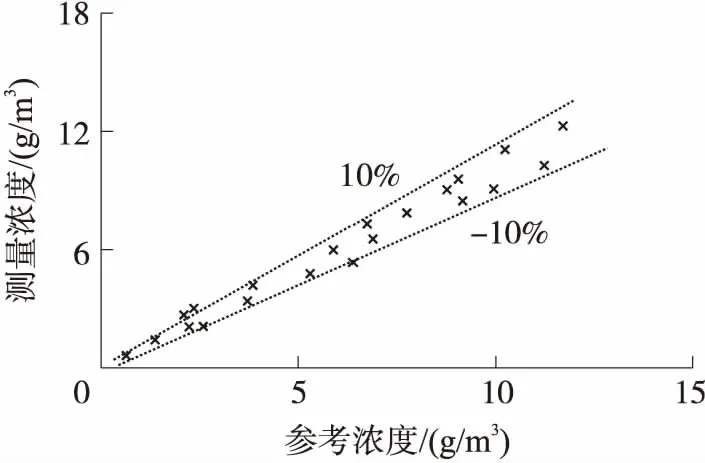
图11 R=0.062 mm测量值与参考值比较图

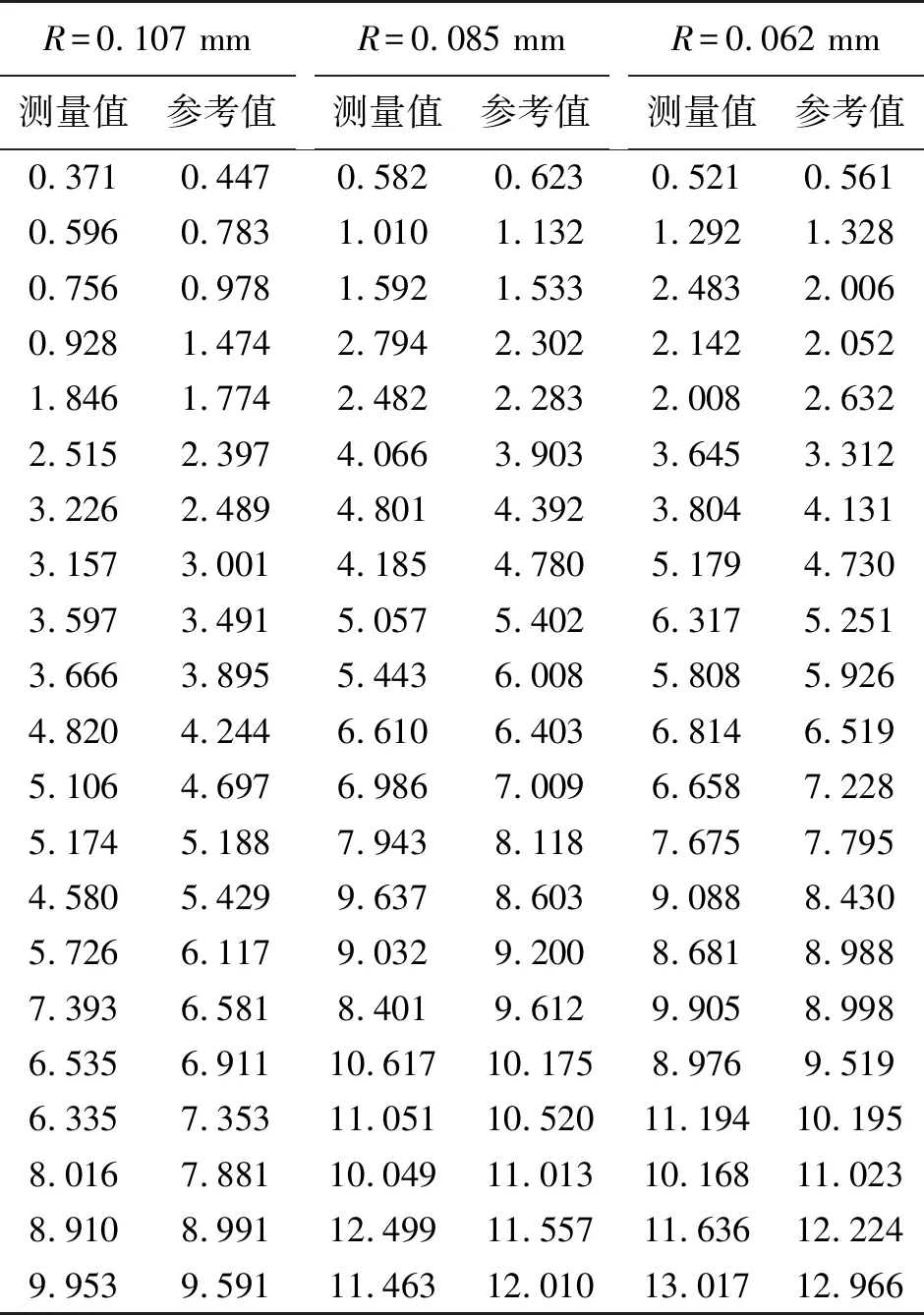
表3 不同粒径下浓度测量值和参考值 单位:g/m3

由图9～图11可得,忽略粗大误差的情况下,在实验范围内,由蚁群算法所得特定粒径分别为0.062 mm、0.085 mm、0.107 mm时,悬移质溶液的浓度测量相对误差范围分别为±10%、±13%、±15%,相比于经验模型法所得浓度测量结果[15]精度有所提高,可见实验浓度测得值与参考值的一致性较好。

4 结论

通过蚁群算法对基于ECAH模型和实验获得的超声衰减系数进行了悬移质溶液浓度参数的反演优化。通过对蚁群算法参数的优化确定了最优参数值分别为:蚂蚁总数为20,蚂蚁最大移动次数为90,信息素挥发系数为0.4,转移概率为0.6,研究表明蚁群算法能够在较短时间内实现全局寻优。将由超声衰减法所得浓度测量结果与烘干法所得的浓度结果进行对比发现,在特定粒径下测量结果的相对误差均在±15%以内,而且随着悬移质粒径的减小测量精度显著提升。实验结果表明文中方案切实可行,运用参数优化的蚁群算法后提高了悬移质浓度的测量精度及测量时效。