Ca0.5Ba0.5MnO3多铁性的第一性原理

金 山, 靳锡联, 焦 正, 孟 醒,

(1. 吉林大学物理学院新型电池物理与技术教育部重点实验室, 长春130012;2. 吉林大学物理学院超硬材料国家重点实验室, 长春130012;3. 上海大学环境与化学工程学院, 上海200444)

ABO3型钙钛矿及固溶结构铁电(ferroelectric, FE)材料因其富含多种独特的物理性质而受到广泛关注. 在各种电子器件向小型化和多功能化发展的过程中, ABO3型钙钛矿材料还因其独特的铁电、铁磁(ferromagnetic, FM)等性质以及各种铁性间可能的耦合协同作用, 成为未来信息存储与探测技术领域的候选材料之一. ABO3型钙钛矿材料的铁电性多来源于阳离子相对对称中心的偏离, 而铁磁性多来源于过渡金属阳离子的d 壳层电子[1-2]. 在已有研究中, 铁电性与铁磁性的耦合虽然在一些材料中有所表现(例如BiFeO3[3]), 但都相对较弱, 不能在磁电调控中实现规模化的商业应用. 因此, 寻求单相中具有强磁电耦合效应的多铁材料已成为多铁领域最重要的研究方向之一.

已知CaMnO3体材料的铁电模声子频率在不同磁构型下变化很大[4], 其八面体的晶体场将Mn 离子的5 个d 轨道劈裂为三重简并的t2g轨道和二重简并的eg轨道. 根据铁电的d0规则, t2g轨道上所占据的3 个电子会增加Mn 离子和氧原子之间的库仑相互作用, 从而抑制电极化的产生[5]. 事实上, G 型反铁磁(antiferromagnetic, AFM)构型下CaMnO3也并没有发生自发极化. Bhattacharjee 等[4]对CaMnO3的研究发现, CaMnO3材料的反铁畸变(antiferrodistortive, AFD)模会抑制铁电模的产生. 所幸的是, AFD 模的频率随着晶格常数的拉伸变化很小, 而铁电模的频率却随着拉伸显著增加. 因此, 在施加较大拉伸应变的情况下,CaMnO3可以出现一定的电极化强度. 同时, 如果将AFD 模对应的扭曲冻结, CaMnO3的铁电性还可以得到显著增加[4]. 结合这个原理, Wu 等[6]利用CaTiO3/BaTiO3超晶格有效地抑制了AFD 模, 并在CaTiO3中实现了较大的铁电性. 在这个研究中, Ba 原子相对较大的原子半径起到了关键的作用.

根据这个思路, 针对CaMnO3体材料, 考虑如果用半径较大的Ba 原子替代Ca, 能否在CaxBa1-xMnO3合金中实现对AFD 模的抑制, 进而增强铁电性？在这种材料中, 铁电性的来源是Mn 离子相对中心位置的偏移, 而Mn 本身是一种典型的磁性材料, 当铁电性实现的时候,如果系统中同时具备较好的铁磁性质, 那么铁电性与铁磁性是否可以实现较好的耦合？

基于这个考虑, 本工作利用第一性原理电子结构计算方法, 通过对CaMnO3, BaMnO3的软声子模式分析, 构造出一种Ca0.5Ba0.5MnO3(CBMO)合金结构(2×2×2 超晶胞, Ca 和Ba 在A 位上以fcc 型进行排布为例, 见图1). 研究发现, 此合金可同时具有基于Mn 原子的铁电性与铁磁性(G 型反铁磁构型下的电极化强度为6.70 µC/cm2, 铁磁构型下的电极化强度为23.214 µC/cm2). 这些性质产生的主要机制是半径较大的Ba 原子使晶格发生应变, 从而产生有效负压, 减弱了CaMnO3的AFD 模对铁电模的抑制, 进而诱导铁电极化. 这些结果意味着当此材料在磁场作用下由G 型反铁磁构型转变为铁磁构型时, 其电极化强度可以发生显著变化. 因此, 它是一个潜在的具有较好磁电耦合性质的材料. 基于第一性原理电子结构计算给出的不同磁结构总能, 本工作还进一步拟合出海森堡模型[7]的参数, 并针对其哈密顿量展开了有限温度下的Monte-Carlo 模拟[8], 模拟出的奈尔温度为70 K, 铁磁相居里温度为61 K. 这些结果从理论层面给出了一种新型的、源于相同原子的, 并可能提供有效铁电耦合的多铁材料. 针对其电子结构进行分析, 也可为今后类似系统的相关实验提供必要的理论参考.

图1 CBMO 结构示意图Fig.1 Schematic diagram of the type of CBMO

1 理论计算方法

本工作基于密度泛函理论, 运用了Vienna Ab Initio Simulation Package (VASP)[9-10]软件包进行计算. 在密度泛函理论的电子交换关联描述中, 本工作采用了PBEsol(the Perdew-Burke-Ernzerh of functional revised for solids)广义梯度近似[11-12]. PBEsol 泛函是对PBE 的进一步修正, 在处理固体材料结构时, 可以得到很接近实验的晶格常数, 从而尽可能地保证结构和电极化强度计算的准确性. 为了更好地处理Mn 的3d 壳层电子, 本工作进一步使用了GGA+U 方法[13], 用到的库仑相互作用项U = 4.0 eV、交换相互作用项J = 1.0 eV. 选择这个两个参数是为了保证晶格常数、带隙和原子磁矩都能很好的匹配实验. 在对CBMO 晶体的计算中, 各原子的价电子组态分别为Ba 5s25p66s2, O 2p6, Mn 2p63d54s2, Ca 4s2. 计算中运用了平面波基矢和投影缀加平面波赝势, 电子迟豫精度为10-7eV, 所有原子坐标和晶格常数都进行自由优化, 截断能和布里渊区采样点数分别为500 eV 和4×4×4.

在电子自发极化强度的计算方面, 本工作使用了Berry-Phase 方法[14-16]. 上述所有计算都是在确保CBMO 的G 型反铁磁和铁磁构型均为具有带隙的绝缘体的情况下进行的, 带隙分别为0.72 eV(G-AFM)和0.003 1 eV(FM). 在合金结构的产生过程中, 本工作运用2×2×2(40 个原子)超晶胞, 结合弛豫软声子的方法计算晶格不稳定性, 优化结构[17-18]. 所有基态性质(如磁构型、电极化强度、电荷密度等)都是通过第一性原理得到.

计算系统的奈尔温度和居里温度时, 本工作基于附加周期性边界条件的12×12×12 的立方格子来进行Monte-Carlo 方法[18]模拟海森堡模型, 模拟温度范围是30～150 K. 运用Metropolis 抽样方法[19]抽样, 累计1 000 000 步.

2 计算结果与讨论

在CBMO 形成合金时, 其结构对称性必然降低, 结构将变得更加复杂无序, 计算复杂且耗时较长. 即使在此基础上求得力常数, 也会产生很大的误差. 本工作首先找出立方结构的CaMnO3, BaMnO3中所有布里渊区中心的铁电模和布里渊区边界的反铁电模的自由度, 并将二者的自由度直接加成, 得到CBMO 合金中所有可以发生的相变自由度. 然后放开所有不稳定的振动模的限制, 对所有原子位置和晶格常数进行自由优化, 从而得到优化好的最终结构.最后, 将此结构做声子谱计算, 以确定其合理性和稳定性.

CBMO 基态磁结构的驰豫基于4 种假设的磁构型进行, 分别为G 型、A 型、C 型反铁磁构型以及铁磁构型. 4 种磁构型的晶格常数、空间群及能量如表1 所示. 结果表明, 在4 种磁构型中, G 型反铁磁构型的能量最低, 是基态自旋构型.

表1 4 种磁构型的晶格常数、空间群及能量Table 1 Lattice constants, space groups and energies of the 4 magnetic ordering types

之后, 本工作利用Berry-Phase 方法计算了fcc 构型的CBMO 超晶格4 种磁构型的电极化强度[14-16], 计算结果如表2 所示, 其中最为关键的是, CBMO 超晶格的不同磁构型都表现出了自发的铁电极化, 极化方向平行于[110]晶向. 从表2 中还可以看出, CBMO 晶体从G 型反铁磁构型到铁磁构型转化的过程中, 电极化强度变化非常大. 这是由CBMO 中很大的自旋声子耦合效应所导致的. 当自旋构型由反铁磁变成铁磁时, 它的铁电模声子会变得更软.

由于Ba2+具有比Ca2+更大的离子半径, 当CaMnO3和BaMnO3结合形成合金时, 合金相当于负静水压下在CaMnO3晶体[4], 而更小的短程斥力和更大的晶格常数则更有利于抑制合金晶体中的AFD 模, 从而减轻AFD 模对铁电模的抑制[4]. 更有趣的是, 这两种复杂过渡金属氧化物的结合, 既可以看成是在CaMnO3的A 位掺入Ba, 成功抑制了CaMnO3反铁电模的冻结, 诱导出现铁电极化, 又可以看成是在BaMnO3的A 位掺入Ca, 有效抑制了BaMnO3室温下没有电极化现象的六角相的产生[1].

表2 4 种磁构型的电极化强度Table 2 Electric polarization of the 4 magnetic ordering types

在比对优化后的G 型反铁磁和铁磁构型的过程中, Mn 离子都偏离中心位置向[111]方向移动, 但是层间Mn 原子在[001]构型方向上的位移相互抵消, Mn 的整体位移为[110]方向. 正是由于Mn 原子偏离中心的行为, 使得CBMO 诱导铁电畸变. Mn 在铁磁构型中的净位移大于其在G 型反铁磁构型中的, 而这与之前关于电极化强度的计算结果一致, 即铁磁构型中的电极化强度(23.214 µC/cm2)大于G 型反铁磁构型中的电极化强度(6.70 µC/cm2).

众所周知, ABO3化合物中O 的2p 轨道和B 位原子的d 轨道之间强烈的杂化现象, 会让两个相邻乃至次近邻的B 位原子之间的的d 壳层电子产生很大的跃迁积分. 根据Anderson-Goodenough-Kanamori 定则[20-22], 这样的现象会大大增加B 位原子间的磁相互作用常数, 从而产生很高的磁有序温度. 本工作希望在CBMO 晶体中也出现较大的反铁磁耦合, 因此利用海森堡模型拟合了它的磁交换常数, 如图2 所示, 其中J1, J2代表平面内、平面间的最近邻磁交换作用, J3, J4表示平面内、平面间的次近邻磁交换作用.

图2 CBMO 锰氧八面体中Mn 原子之间的磁交换作用Fig.2 Magnetic exchange effect between Mn atoms in CBMO oxygen octahedra

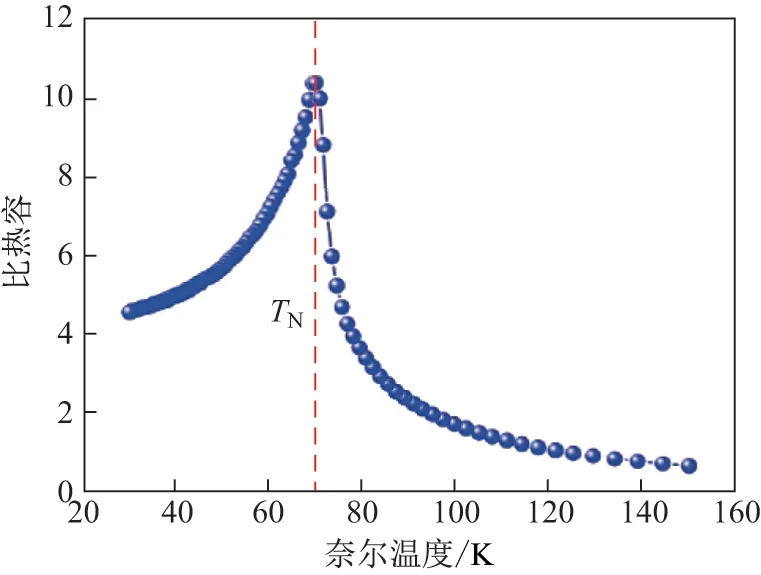
图3 Monte-Carlo 模拟的相变温度Fig.3 Phase change temperature resulted from Monte-Carlo simulation

3 结束语

本工作利用第一性原理电子结构计算方法, 通过对CaMnO3, BaMnO3的软声子模式分析, 构造出一种CBMO 合金结构. 结果发现，此合金可同时具有源于Mn 原子的铁电性与铁磁性. 它在基态G 型反铁磁构型下的电极化强度为6.70 µC/cm2, 亚稳态铁磁构型下的电极化强度为23.214 µC/cm2. 这些铁电性的产生是因为半径较大的Ba 原子可导致晶格发生应变,产生有效负压, 减弱CaMnO3的AFD 模对铁电模的抑制, 进而诱导铁电极化. 这些结果意味着, 这种材料在磁场的作用下由G 型反铁磁构型转变为铁磁构型时, 电极化强度可发生显著变化. 针对磁性性质, 本工作还进一步利用海森堡模型展开了有限温度下的Monte-Carlo 模拟,模拟出的奈尔温度为70 K, 铁磁相居里温度为61 K. 这些结果从理论层面提出了一种新型的、源于相同原子的, 并可能提供有效磁电耦合的多铁材料. 与此同时, 关于铁电性产生机制的分析还意味着可以通过在A 位掺杂较大半径金属的方法, 在类似材料中达到增强合金材料磁电耦合效应的目的.

致谢感谢吉林大学高性能计算中心提供的计算平台!