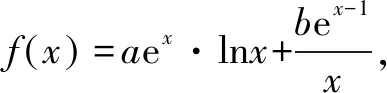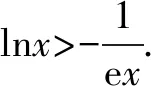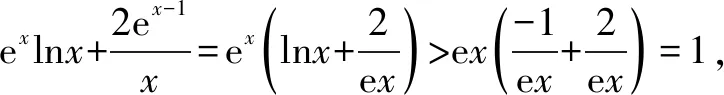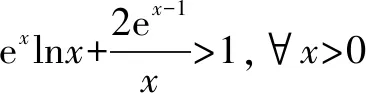高等数学视野下的高中数学
——议泰勒公式在高考中的应用
2019-09-19孙博
孙 博
(浙江省永康市第一中学 321300)
一、引言
1.泰勒公式
在初等函数中,多项式是最简单的函数.因为多项式函数的运算只有加、减、乘三种运算.如果能将有理分式函数,特别是无理函数和初等超越函数用多项式函数近似代替,而误差又能满足要求,显然,这对函数性态的研究和函数值的近似计算都有重要意义.
若任意一个函数f(x)(不一定是多项式函数),只要函数f(x)在a存在n阶导数,总能形式地写出一个相应的n次多项式

定理1(泰勒定理)若函数f(x)在a存在n阶导数,则∀x∈U(a),有
f(x)=Tn(x)+ο[(x-a)n],(1)
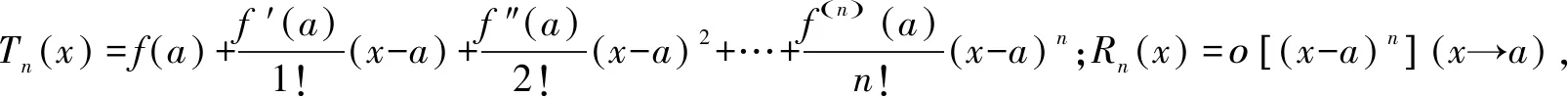
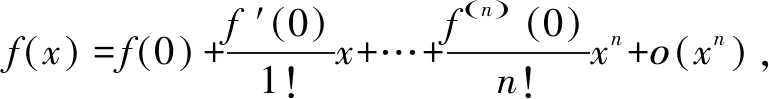
2.泰勒公式常用的几个展开式
二、高考中的泰勒公式
例1 (2015年福建高考数学第20题)已知函数f(x)=ln(1+x),g(x)=kx(k∈R),
(1)证明:当x>0时,f(x) (2)证明:当k<1时,存在x0>0,使得对任意x∈(0,x0),恒有f(x)>g(x); (3)确定k的所有可能取值,使得存在t>0,对任意的x∈(0,t)恒有|f(x)-g(x)| 分析与解答在(1)问中,高考的标准答案是构造函数,利用导数求函数的单调性,求出函数上界,进而证明出不等式的成立,证明如下: 令F(x)=f(x)-x=ln(1+x)-x,x∈(0,+),则有 当x∈(0,+)时,F′(x)<0,所以F(x)在(0,+)上单调递减,故当x>0时, F(x) ex>1+x,当x>0时,不等式两端同时取以e为底的对数并化简得x>ln(1+x),得证.这就是含有高等数学知识中泰勒公式身影的一道高考题目,了解题目的起源,会更加透彻的看清题目的内涵,其余各问迎刃而解. (1)求a,b; (2)证明:f(x)>1. 分析与解答在(2)中,要证明不等式的成立,参考答案给出了构造函数求导证明的思想方法,这道题目有泰勒公式的背景,可以利用泰勒公式得出的不等式来进一步转化与证明,如下: 因为由泰勒公式得ex>1+x,x>0, ① 以泰勒公式为背景的不等式经过转化与变形,便可以在相应题目中得以“秒杀”,很大程度上简化解题步骤. 总之,从以上具体的高考真题实例的探究与发现中,在高等数学视野下,利用泰勒公式来解决高考函数中的有关不等式问题主要是实现将超越不等式转化为代数式不等式,既简化了运算过程,又为高考中的函数不等式问题的解法注入了新的活力并充分展现了泰勒公式无尽的魅力,对数学核心素养的落实起到重要作用.