追本溯源 教学相长——2019浙江数学高考第21题

胡孟君

(浙江省绍兴市越州中学 312000)

2019年是浙江省高考改革数学文理合卷考试的第三年，试卷严格遵循《2019年浙江省普通高考考试说明》和《浙江省普通高中学科教学指导意见》的要求，全面覆盖高中数学基础知识，突出主干知识，重视知识的内在联系，秉承了“简约而不简单”的风格.试题面向全体考生，为不同基础、不同能力水平的的考生都提供了适当相应的思考空间，体现了较好的区分度.本文以2019年浙江高考第21题为例，从试题背景、结构分析、试题解法等多方位进行研读，希望对平时的教学有所启示.

一、试题呈现

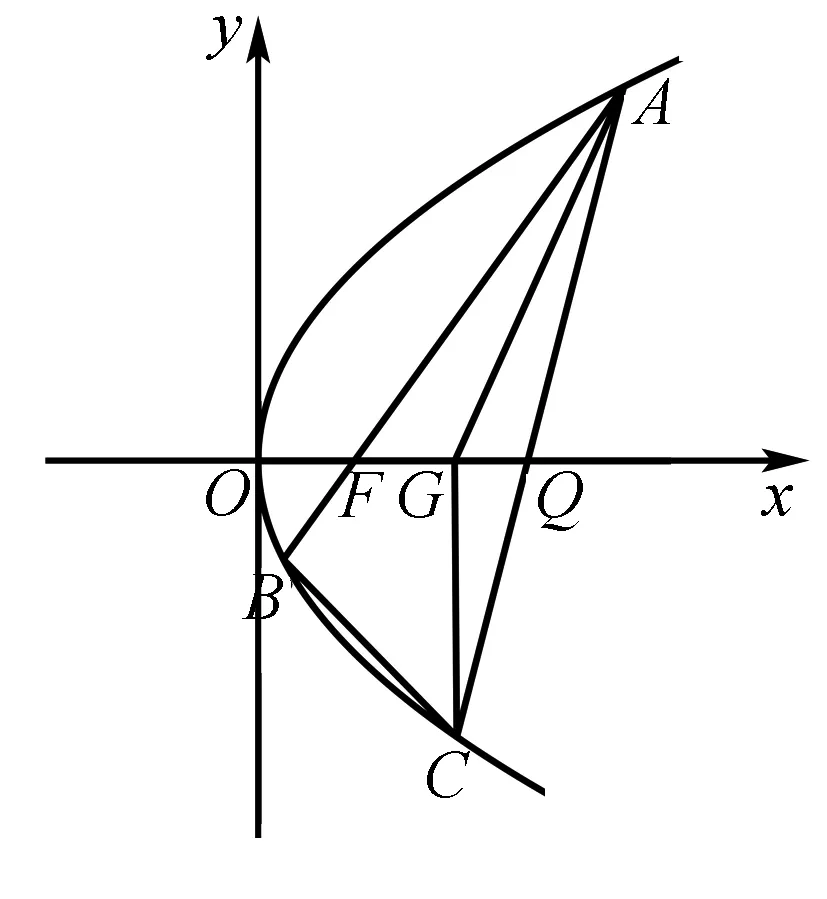
(本题满分15分)如图，已知点F(1, 0)为抛物线y2=2px(p>0)的焦点．过点F的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧．记△AFG，△CQG的面积分别为S1,S2．

(1)求p的值及抛物线的准线方程；

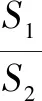
二、试题背景

这是一道圆锥曲线的综合题，本题以抛物线为载体，常见的问题为基础，常用的方法为手段来设计问题，引入新的几何背景和设问方式，叙述简洁清楚，很好地呈现了浙江省试题命题“简约而不简单”的风格.

第一问易得p=2，抛物线的准线方程x=-1.所以，后面的篇幅我们将围绕第二问进行.

三、结构分析

条件：

1.抛物线的方程y2=4x.

2.AB为过焦点的弦，C为抛物线上的点，Q为AC与x轴的交点.

3.△ABC的重心G在x轴上.

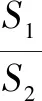
数据分析完成第一小题完成韦达定理得到面积比的函数182200732009200

学生思维的难点

上表是选取本校数学成绩较好的200位同学作的一项调查.通过调查发现，学生思维的难点主要表现在以下几个方面：

1.△ABC的重心G的转化.

3.运算能力.高考对圆锥曲线的考查主要体现在两个方面：

①转化能力；

②运算能力.

在解决圆锥曲线的综合题时，能探索出解题思路，已经跨出了一大步，但是离最终的胜利却仍然面临一个巨大的挑战——计算问题.所以寻求简捷合理的有效途径，优化计算过程，显得尤为重要.

四、试题解法

1.代数法——设点

代数法的特点是，直译题意，顺势而下.方法如下：

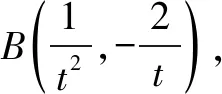
令m=t2-2，则m>0，

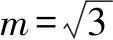
点评这是考试院给出的答案.这种解法很好地体现了浙江高考对解析几何大题的定位：考查学生用坐标法解决几何问题的能力和学生的运算能力，同时降低了计算的难度.

2.代数法——设直线

根据对称性，下设y1>0，

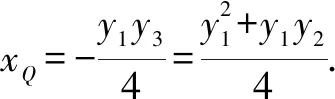
设AB直线方程：x=my+1(m≠0，若m=0则y3=0不符合题意)，

点评解析几何常见的方法是设点设线，很多同学总是举棋不定，实际上这两种方法是相通的，重要的是理清变量之间的关系，当然还要有过硬的运算功底.

3.几何法

由重心的性质，可知S△ABG=S△ACG

设A(x1,y1),B(x2,y2),C(x3,y3)(y1>0>y2)，

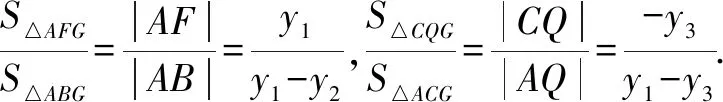
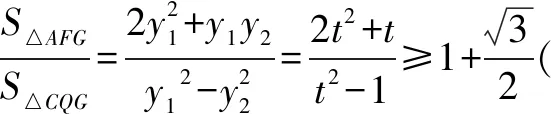
点评这种解法利用平面几何的性质，将两个三角形的面积比转化为线段长度之比，然后将其转化为纵坐标之间的关系，很大程度上简化了前面代数法中所带来的繁杂的计算，提高了解题效率.

4.向量法

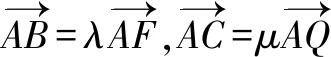
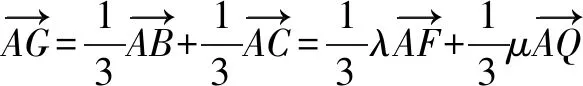
由F,G,Q三点共线，得λ+μ=3(1<λ,μ<2).

因为G为△ABC的重心,所以S△ABG=S△ACG.

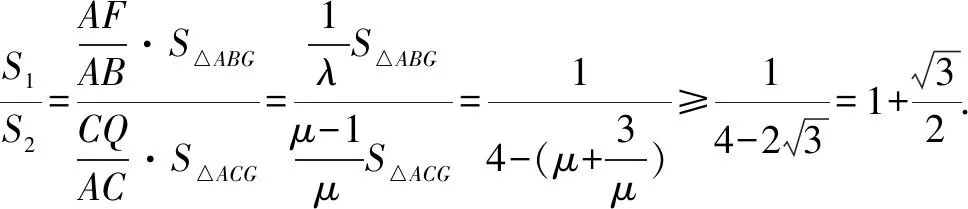
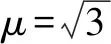
点评这种解法很好地利用向量是代数和几何的综合体的特性，把几何与代数完美地融合在一起.

纵观本题的四种解法，前两种解法是解析几何中的通法，是解决直线与圆锥曲线位置关系的常用方法，将两个三角形的面积的比值表示成某一个参数的解析式，进而转化为求函数的最值问题.解法三、四通过数形结合，大大简化了计算，这也要求我们教师在教学过程中要重视问题的几何表征和代数特征，以及两者之间的转化.

五、总结与思考

从上述的四种解法中，我们深切地感受到，“想得少一点，做的多一点，想得多一点，做的少一点”，这是近几年浙江高考命题的一个理念.正确计算是解决解析几何问题的基本功，数形结合是转化几何问题的出发点.若想在现今的高考中所向披靡，两者缺一不可，我们给出以下建议：

1.对于学生

(1)重视运算能力

运算能力包括基本的计算与算法的选择两个维度.例如本题中已知直线过某个定点与抛物线相交，两个交点坐标之间的关系，这是基本的计算，必须熟练掌握.另外，在进行复杂的运算之前，要有算法选择意识，想清楚计算的过程，选择尽量优化的算法和顺序再动手.

(2)强化数形结合思想

解析几何的本质是用代数的方法解决几何问题，但并不排斥对图形结构的分析，若能运用好数形结合思想，先从图形上将问题转化，再计算则会简单很多.

(3)选定一个方向，做下去

解析几何计算的繁杂是常态！与其“望而却步”，不如“埋头实算”，你要坚信，只要方向正确，题目一定是可以解决的，不要轻易地半途而废.和任何事情一样，数学解题也是一个充满喜怒哀乐的过程，惟有坚持，才能品尝到成功的喜悦！

2.对于教师

(1)变式教学，提升学生素养.对高考题进行拓展性研究，触及数学的本质，通过改变题目条件、把平面几何性质迁移至圆锥曲线中等方式编制适合学生练习的新题，提高学生分析、解决问题的能力，提升数学核心素养.

(2)解法探析，智慧碰撞.教学中既要注重通法教学又要学会跳出模块限制(例如本题圆锥曲线)，站在其他知识(平面向量，三角函数，不等式等)的视角审视问题，或许会有一番别开生面的场景.