错中悟道——一道不等式例题的教学感悟

江中伟

(广东省梅州市虎山中学 514299)

一、问题提出

这是笔者近期高一随堂听课时一位年轻教师所采用的一道例题. 学生思考片刻后，教师让学生A在黑板上书写他的解答过程.

解答过程如下：

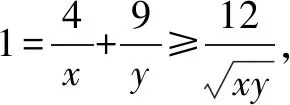
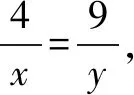
最后教师强调：若多次利用基本不等式求最值时，必须保证每一次取得等号的条件要一致，否则就会出错.

教师点到为止， 然后进行第二题的讲评.笔者认为教师应该趁热打铁，引导学生进行一题多解和多题一解的探究，培养学生的数学核心素养.

二、解法探究

为方便表述把刚才上面的正解记为解法1. 教师可以引导学生观察题设中的x和y的关系，y可以看作是x的函数，从而得到解法2.

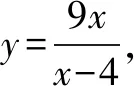
教师引导学生联想初中学过的因式分解公式ab+a+b+1=(a+1)(b+1)，从而得到解法3.

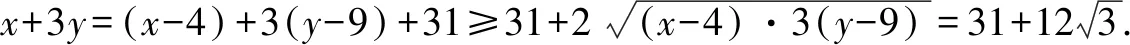
教师再引导学生从“1”出发联想到三角公式：sin2α+cos2α=1，则可以得到解法4.

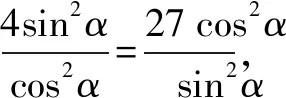
教师继续引导学生：能否引进一个参数t，消去变量x，代入题设条件中得到一个含有参数t关于变量y的一元二次方程，从而得到解法5.

由已知得xy-9x-4y=0，令x+3y=t，得x=t-3y，代入上式得到方程：

3y2-(t+23)y+9t=0有实根.

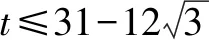
这样，教师引导学生从不同角度、多种方法解答问题，既帮助学生巩固了以前学过的知识和方法，又提高了学生的解题能力和培养了学生的数学核心素养. 另外为了方便学生掌握这些解题方法，教师可以给方法1命名为“1”的妙用，方法2命名为“函数法”， 方法3命名为“整体处理法”，方法4命名为“三角代换法”, 方法5命名为“判别式法”. 如模型：设实数x,y满足方程ax2+bxy+cy2+dx+ey+f=0，求mx+ny的最值(其中a,c∈R+，b,d,e,f,m,n∈R). 此类题型的通法是：可令mx+ny=k，与方程ax2+bxy+cy2+dx+ey+f=0联立， 消去变量y(或x)后，得到关于变量x(或y)的一元二次方程，利用一元二次方程有实根的必要条件(判别式大于或等于零). 这样， 对于具体的问题学生就能快速合理地选用恰当的方法.

三、触类旁通

教师还可以趁热打铁出示下列几组练习题，以检验学生学习的效果.

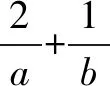
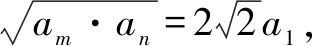
7.(2010年高考重庆卷理科第7题)已知x>0，y>0，且x+2y+2xy=8，则x+2y的最小值为(B).

四、教学感悟

美国著名数学教育家波利亚说“一个专心的认真备课的教师能够拿出一个有意义的但又不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.”因此，在平时的教学中，挑选恰当的题目进行一题多解、多题一解，能够充分调动学生的学习兴趣，激发学生的思维灵感，促使学生在原有的基础上进行再认知，深化理解知识间的联系，从而达到复习知识，优化结构，探究方法，提升能力的目的；另一方面也可以使学生在系统的高度上来审视问题，理顺思维方向，优化解题思路. 无疑，这对于学生数学核心素养的培养和提升有着十分积极的作用.

核心素养是高中教育教学的灵魂，尤其是高中数学学科更是学生核心素养的重要阵地. 因此在高中数学课堂教学中应充分体现学生的主体参与过程，不能是教师的一言堂. 因为“告诉我，我会忘记；分析给我，我可能记住；如果让我参与，我会真正理解.” 通过一题多解和多题一解训练，激发了学生的探究兴趣和参与意识，使得学生有了创新的冲动，化被动为主动参与、积极探究.

因此我们教师在日常的教学中，应引导学生多方面、多角度思考，引导学生经历用不同方法解决数学问题以及用相同方法解决同类数学问题(即一题多解和多题一解)，才能有利于学生开拓数学视野 ，为学生的终生发展、持续发展、多元发展奠定良好的基础.