利用递推关系求解数列通项公式的解题策略
2019-09-19许万成
许万成
(江苏省建湖县第二中学 224700)
数列问题一直是高考的热点,也是难点.很多学生对数列都存在畏惧心理.其根本原因是他们对于数列的通项公式不够了解,如果能够把数列的通项公式求出来,那么很多问题都可以解决了.但是数列的通项公式如何求解呢?尤其是已经知道数列的项之间的递推关系,如何快速准确地求出数列的通项公式又成为解决问题的关键.本文笔者根据自己平时的教学,将一些常见的题型利用例题的形式呈现给读者.
一、形如an+1=pan+q型
例1已知数列{an}满足a1=1,an+1=3an+1,求数列{an}的通项公式.
解因为an+1=3an+1,



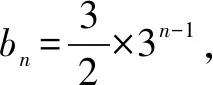
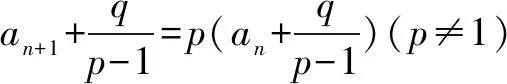
二、形如an+1=pan+qn型
例2已知数列{an}满足a1=1,an=3n+2an-1(n≥2),求an.
解因为a1=1,an=3n+2an-1(n≥2),
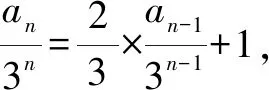
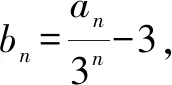
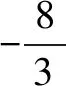


三、形如an+1=pan+an2+bn+c(p≠1,0;a,b,c为常数)型
例3已知数列{an}满足a1=1,an+1=3an+2n-1,求an.
解因为a1=1,an+1=3an+2n-1,
所以an+1+(n+1)=3(an+n).

所以数列{bn}是以2为首项,3为公比的等比数列.
即bn=2×3n-1,故an=2×3n-1-n.
例4已知数列{an}满足a1=1,an=3an-1+2n2-1(n≥2),求an.
解因为an=3an-1+2n2-1(n≥2),
设an+xn2+yn+z=3(an-1+x(n-1)2+y(n-1)+z),整理得an=3an-1+2xn2+(-6x+2y)n+(3x-3y+2z).



评注这种类型一般利用待定系数法构造等比数列,即设an+1+x(n+1)2+y(n+1)+z=p[an+xn2+yn+z]与已知递推式比较,解出x,y,z,从而转化为公比为p的等比数列{an+xn2+yn+z}.
四、形如an+2=pan+1+qan(其中p,q均为常数)型
例5已知数列{an}满足an+2=5an+1-6an,a1=-1,a2=2,求数列{an}的通项公式
解设an+2+λan+1=(5+λ)(an+1+λan),比较系数可解得λ=-3或λ=-2.
不妨取λ=-2(取-3,结果形式可能不同,但是本质相同),则有an+2-2an+1=3(an+1-2an),则{an+1-2an}是以4为首项,3为公比的等比数列.
所以an+1-2an=4×3n-1.
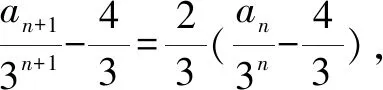
评注对于an+2=pan+1+qan(其中p,q均为常数)可以将递推公式转换成an+2+λan+1=(p+λ)(an+1+λan)形式,比较系数可求得λ,然后设bn=an+1+λan,可以发现数列{bn}为等比数列,求出数列{bn}的通项公式,接着利用例2的方法求解数列{an}的通项公式.
五、形如为常数)型
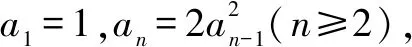

所以log2an=1+2log2an-1,
即log2an+1=2(log2an-1+1).
设bn=log2an+1,则数列{bn}是以1为首项,2为公比的等比数列.
bn=2n-1,故an=2(2n-1-1).

