用金刚石磨头数控加工轴对称非球面光学玻璃透镜
2019-09-19陈宏堃沈剑云
曾 凯, 陈宏堃,沈剑云, 吴 贤, 鲁 浪
(华侨大学 机电及自动化学院, 福建 厦门 361021)
在光学系统中应用非球面元件,可以增加光学设计自由度,修正像差,改善系统成像质量,极大减小光学系统的外形尺寸和质量[1]。基于此,非球面光学元件在中小型民用光学产品上应用越来越普及,如各种日用高品质照相机、刻录机光头、光学显微镜以及显示投影仪等设备中都可见非球面镜的身影[2-3]。
近年来,非球面光学元件的加工技术有了显著的发展,其加工方法主要有:数控研磨抛光技术、单点金刚石车削技术、离子束加工、模压成型等,不同的加工方法都有各自的优缺点[4-5]。使用数控研磨抛光技术加工非球面镜时,通常会先加工出非球面光学元件最接近球面的一面,然后再按照该面磨削出球面,最后通过研磨和抛光加工出符合要求的非球面;但这种方法耗时太长,生产效率较低[6]。单点金刚石车削技术主要用于有色金属材料如硬铝、黄铜、无氧铜等的典型零件的切削,在切削过程中易发生刀具偏置,往往需要配上在线检测设备才能获得理想的非球面精度[7]。离子束加工虽然可以获得精度较好的非球面,但加工设备和成本较高,且加工设备不具有通用性,因而限制了它的推广使用[8-9]。模压技术主要用来批量制备微小型的非球面透镜,但该技术对金属模具的精度要求很高[10-11]。因此,日用中小型非球面镜的高效、低成本加工技术仍然在不断的探索和研究之中。
目前,为了缩短非球面透镜的加工周期,人们开始采用直接磨削的方法,即在磨削阶段直接加工出符合非球面方程的非球面透镜,该方法因加工效率高、经济性好已经逐渐被广泛使用[12]。为此,以K9光学玻璃为研究对象,结合工程实践对K9高次轴对称非球面进行快速磨削加工,探究不同加工路径对非球面磨削加工的影响;检测不同路径下的K9非球面法向轮廓度误差;根据法向轮廓度误差相关规律,提出一种改变最大有效切削半径的补偿方法,以获得更高精度的非球面表面轮廓。
1 轴对称非球面理论描述
光学系统中,球面透镜聚焦时存在球面像差,使光线无法聚焦于一点而影响成像。而非球面透镜的面型由一系列函数控制,球面各点的曲率不同,因此可以修正球面像差,将光线聚集于一点。在光学系统中,通常用多个球面透镜组合以消除球面像差,但使用非球面透镜则可以替代多个球面透镜,减少透镜数量,简化系统结构,而达到同样的成像效果。
轴对称非球面最常见的是以二次方程或高次方程曲线为母线,绕自身的对称轴旋转形成的回转表面。轴对称非球面方程的描述形式有多种,国际上通用的轴对称非球面母线函数方程[13]为:
(1)
式中:z(x)表示入射光线在非球面上与顶点之间的高度;x表示对应的入射光线在非球面上与旋转对称轴Z的距离;c为非球面曲线顶点曲率;k为非球面曲线二次项系数(k=-e2,e表示离心率);Ai为曲线高次项系数,xi表示曲线高次项,n为最高次项指数。简单来说,e2<0时,非球面的面型是以短轴为对称轴的椭圆球面;e2=1时,非球面为抛物面;e2=0时,非球面则为球面;当0
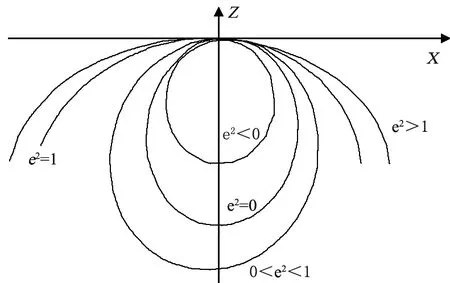
图1 常见二次曲面类型
2 非球面加工实验条件与方案
2.1 实验条件
轴对称非球面铣磨加工在三轴数控加工中心上进行,该机床加工精度可达1 μm,铣磨加工条件如表1所示。其加工原理是以铣磨头代替铣刀,利用磨头上的微细金刚石磨粒进行磨削加工,实验用铣磨磨头为市售电镀金刚石磨头。
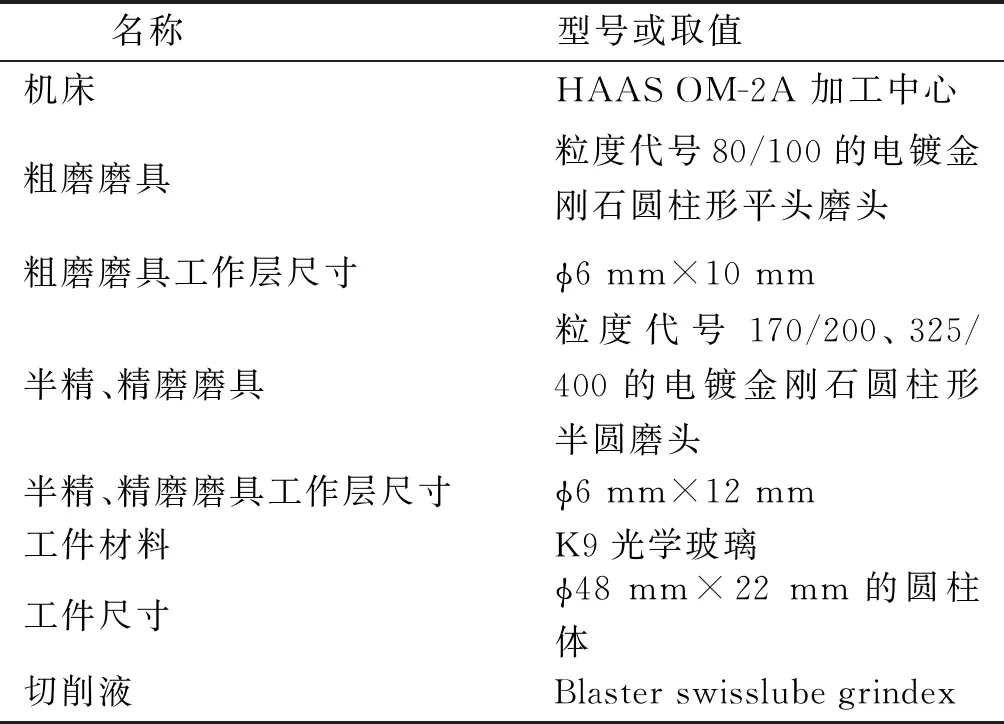
表1 轴对称非球面铣磨加工条件Tab. 1 Conditions of axisymmetric aspheric grinding
2.2 工件铣磨参数设定
在进行非球面快速成型铣磨时,应根据不同工序选择不同的加工参数。一般地,加工工序不同磨头选用的磨料粒度也不同,而加工工序又可分为粗磨和精磨2个阶段。为使非球面达到更高精度,本实验拟将铣磨工艺流程分为粗磨、半精磨、精磨3个阶段。非球面粗磨是为了快速去除工件材料的加工余量,提高后续加工的效率,因而使用粒度代号80/100的平头电镀金刚石磨头;半精磨和精磨则是依次修整粗磨后的非球面面型精度,分别使用粒度代号为170/200和325/400的半圆头电镀金刚石磨头(表1所示)。非球面铣磨参数如表2所示。
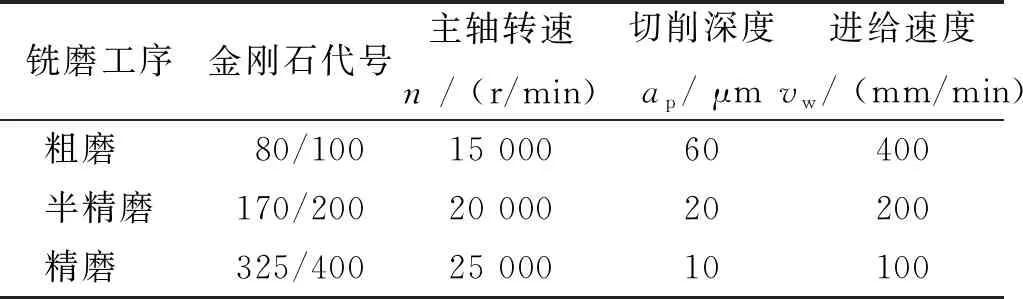
表2 非球面铣磨工艺参数Tab. 2 Aspheric milling process parameters
2.3 工件加工轨迹确定
在本实验实例中,所加工的非球面为φ48 mm的高次轴对称非球面,其非球面曲线方程由工厂设计,具体参数为:c=0.048 30,k=-1,四次项系数A4=-1.361×10-6,六次项系数A6=-5.082×10-9,其余系数均为0。三轴数控铣床加工该非球面时,由于数控程序复杂,因此直接使用PowerMill软件自动生成所需加工程序。建立好如图2所示的非球面模型后,需要给表2的加工工艺参数设置刀具轨迹。其中,粗加工刀具路径选择为模型区域清除;半精加工刀具路径选择为平行精加工;同时为了更好地分析统计误差,方便后续的补偿实验加工,综合考虑之后,在精加工时选用平行精加工和等高精加工2种不同的精加工轨迹进行对比实验,其生成的相应加工轨迹如图3所示。

图2 非球面模型
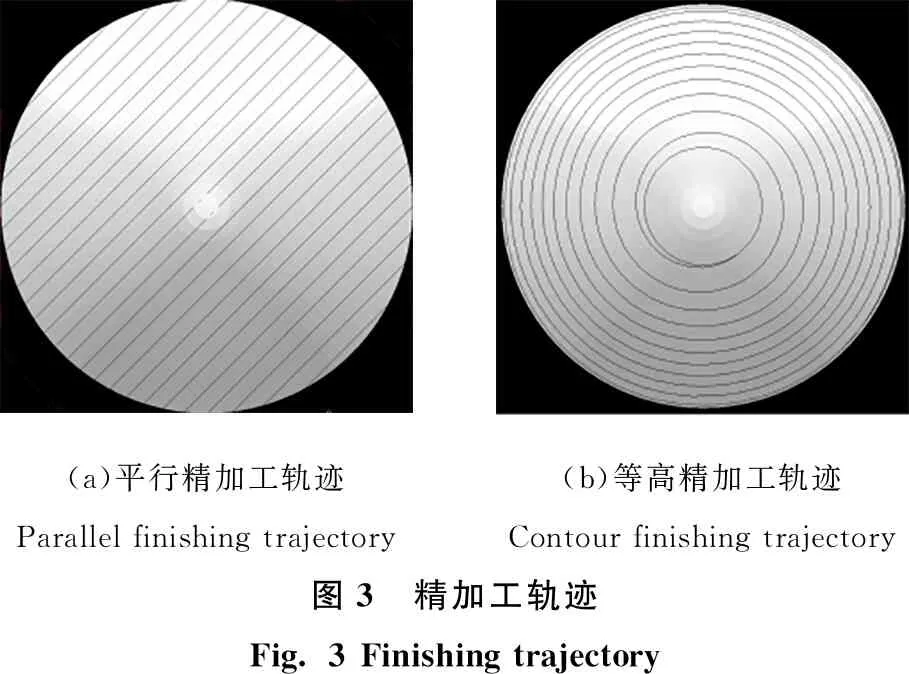
(a)平行精加工轨迹(b)等高精加工轨迹Parallel finishing trajectoryContour finishing trajectory图3 精加工轨迹Fig. 3 Finishing trajectory
加工程序和轨迹确定后进行实际加工,铣磨加工实验平台如图4所示。其中,测力仪的用途是辅助定心,并提高对刀精度。

图4 轴对称K9非球面铣磨工作图
3 实验结果及讨论
3.1 非球面铣磨的法向轮廓度误差
依照表2的工艺参数,在三轴数控加工中心上对K9光学玻璃进行非球面铣磨加工。在完成K9玻璃的粗磨和半精磨后,精磨选取图3所示的2种不同方式。精加工完成后,2种精加工的非球面实物如图5所示。

图5 加工的非球面实物
精加工后的非球面需要进行面型精度检测,其检测方法分在线检测和离线检测2种,且两者都是通过误差补偿来达到减小误差的目的。由于非球面在线检测成本较高,难度较大,因此采用型号为ridge-Global-Status-7.7的三坐标测量机(最大误差2 μm)、按照ISO10360-2标准进行检测。由于三坐标测量结果是非球面的理论坐标值和实际坐标值,以及与之对应的沿X、Y、Z方向的误差,并不能反映非球面的真实法向轮廓度误差,所以需要通过计算来获取非球面不同接触点的法向轮廓度误差。
非球面三维示意图及二维误差放大图如图6所示。要计算非球面不同接触点的法向轮廓度误差,就是要计算图6b中的T值(即图6b中AC线段的长度)。
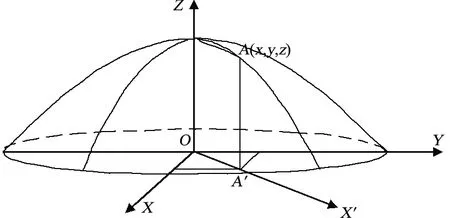
(a)非球面三维示意图
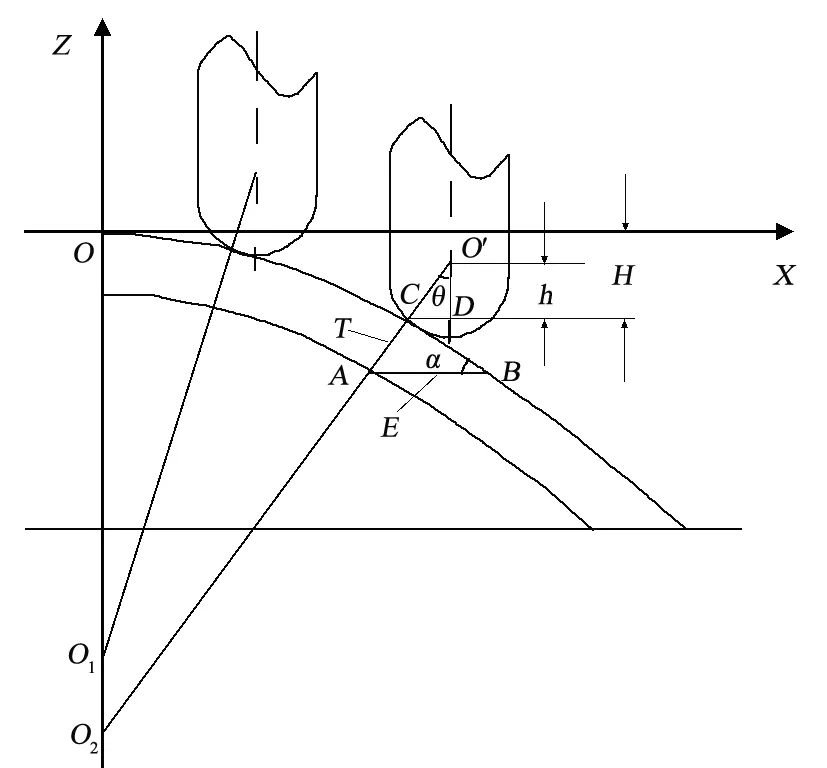
(b)非球面二维误差放大示意图
以图6a的测量点A为例来分析非球面的法向轮廓度误差。假设测量点的坐标为A(x,y,z),则同一高度下相应的理论坐标值为B(x1,y1,z1),将A点坐标投影到XOY平面,则相应的A′O的实际和理论长度分别为:
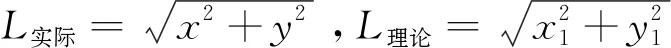
(2)
图6a中正视平面OA′A所在的坐标系为X′OZ,则在非球面坐标系中A点的横坐标为图6a中A′O的长度L,而图6b中的A点和B点分别为三坐标测量的实际点和理论点,其相应的非球面半径偏差为:
E=L实际-L理论
(3)
对非球面函数方程(1)进行一次求导,可以计算出非球面任意点处的切线斜率:
(4)
由于非球面的法向轮廓度误差T的长度是微米级别的,因而可将图6b的弧线BC近似看作直线,即是非球面理论曲线在C点的切线段,而AC为非球面实测曲线在C点的法线段,且AC⊥BC,则由三角形几何关系可得:
(5)
于是有:
(6)
在本次实验中,二次项系数k= -1,代入式(6),进一步化简可得:
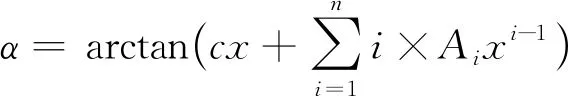
(7)
而图6b中,非球面各点的法向轮廓度误差T有:
T=E×sinα
(8)
因此,通过三坐标测量机可以测量非球面任意点的坐标值,进而通过式(3)得到任意点的E值,再通过式(7)计算出任意点的α值,最后由式(8)计算出任意点的法向轮廓度误差T。
图6b中的高度H为非球面任意点在Z轴方向上与顶点的距离。在计算出精加工后非球面的法向轮廓度误差后,整理数据可得不同高度H下对应的非球面法向轮廓度误差,如图7所示。
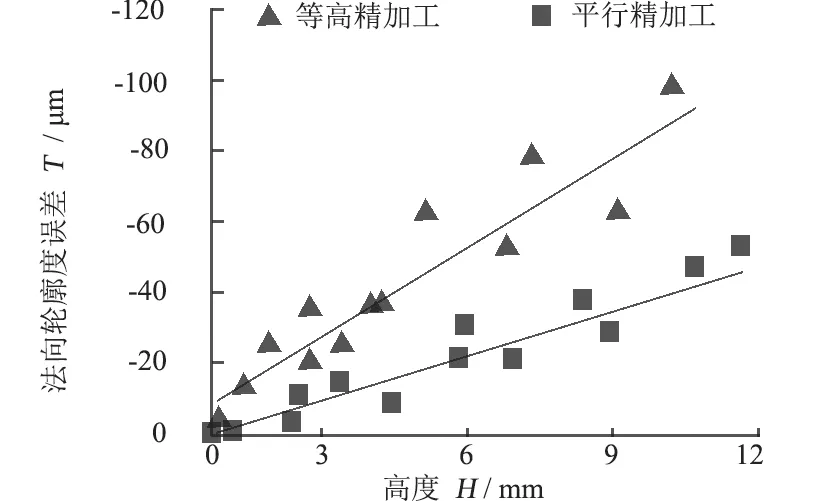
图7 不同高度下的非球面轮廓度误差
通过图7数据发现:2种精加工方式下,高度H增加,非球面的法向轮廓度误差T都会逐渐增加;相较于平行精加工,等高精加工条件下的上升趋势更明显,即平行精加工条件下加工的非球面法向轮廓度误差比等高精加工条件下的要低。在检测中,评定非球面面型精度的参数有2个:一是最大轮廓度偏差PV,定义为法向轮廓度误差T最大值和最小值的差值;二是误差平均值RMS,定义为轮廓度误差T的平均值。将数据进一步整理,可得平行精加工条件下的非球面最大轮廓度偏差PV为54.48 μm,误差平均值RMS为22.88 μm;等高精加工条件下的PV为98.46 μm,RMS为28.88 μm。这一结果与图7的结论相符,即平行精加工条件下的非球面面型精度要比等高精加工条件下的非球面面型精度更高。
3.2 非球面加工中不同接触点的切削线速度
如前所述,选取的精加工路径不同,都会出现轮廓度偏差T随高度H增大而增大的规律。这是由于用表2的参数铣磨加工非球面,虽然每次刀具的下切深度ap、主轴转速n及进给速度vw均保持恒定,但加工过程中工件的不同接触点的有效切削半径不同,其对应的线速度不同造成的。已有的研究表明[11]:在微切削加工非球面光学玻璃中,随着砂轮相对线速度的增大,非球面切削的表面质量降低,且在相对线速度增大的位置,产生大量的脆性崩碎。因此,由于加工中不同接触点的切削线速度不同,有效切削半径不同,可能使三轴数控加工的自由曲面产生误差。
如图6b所示:当刀具加工至刀触点C时,此时的刀位点为O′,两点的连线与刀具主轴轴线的夹角为θ,CD与刀具主轴轴线垂直于点D,O′D的长度等于刀触点C与刀位点O′的轴向距离,将其定义为刀位。若球磨头的半径O′C=r,有效切削半径CD=r1,刀位O′D=h,接触点C的有效切削线速度为vc,则加工过程中任意接触点的刀具有效切削半径r1、刀位h、线速度vc与夹角θ的函数关系如下:
r1=r×sinθ
(9)
h=r1×cotθ
(10)
vc=2πr1n=2πrn×sinθ
(11)
由于图6b中AB与CD平行,所以ΔABC与ΔCO′D相似,α与θ值相等。因此,由式(7)和(11)得到不同接触点的线速度为:
(12)
由式(12)明显看出:在球磨头半径r一定的情况下,加工过程中接触点的有效切削线速度随接触点有效切削半径增大而增大,且随x的增大而增大。
根据非球面母线函数方程(1)和式(12),可以求得距离非球面顶点高度H的原始接触点的有效切削线速度vc,结果如表3所示。表3表明:有效切削线速度随高度H的增大而逐渐增大;且加工非球面工件底部(H=12.0 μm)时的线速度比加工非球面顶端(H=0.3 μm)时的增大约3.76 m/s。
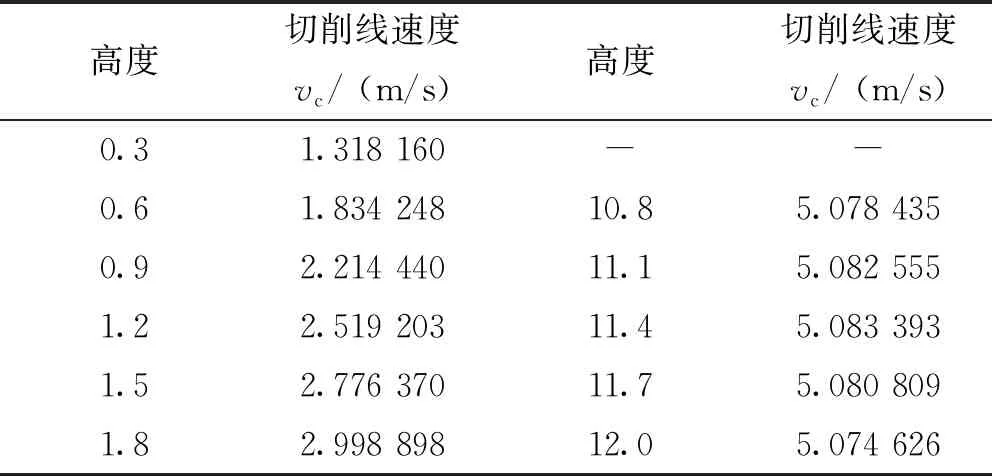
表3 原始接触点的线速度Tab. 3 Linear velocity of original contact point
3.3 非球面加工中磨头的轮廓优化
如前所述,磨头的有效切削半径改变可以对非球面轮廓度误差产生影响。因此,通过优化磨头轮廓,对磨头接触点的有效切削半径进行补偿,可以改变非球面的轮廓度误差。优化磨头轮廓的步骤如下:首先确定标准磨头的有效切削半径r1与非球面轮廓度误差T的函数关系,再将该结果应用于磨头轮廓的优化补偿。
图8为非球面轮廓度误差与有效切削半径之间的关系。如图8所示,从三坐标测量得到的非球面数据提取标准磨头有效切削半径r1与非球面轮廓度误差T数据,离散处理后的线性拟合曲线为:
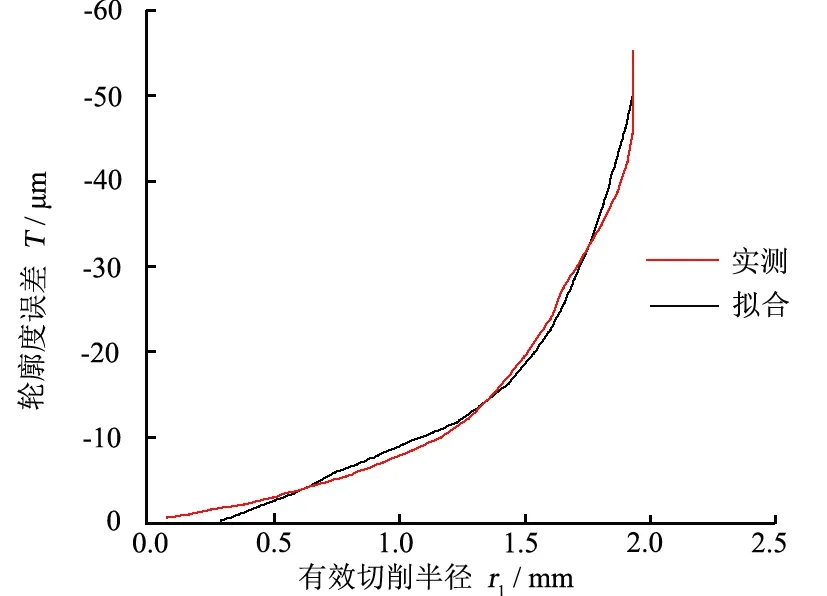
图8 非球面轮廓度误差与有效切削半径之间的关系 Fig. 8 Relation of profile error of aspheric surface varied with effective cutting radii
(13)
拟合曲线(13)的相关系数R2=0.9828,表明该曲线拟合良好。对式(13)求导,得到:
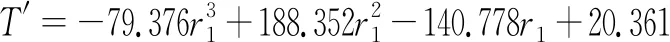
(14)
式(14)中的导数反映了非球面轮廓度误差随铣磨刀具有效切削半径变化的变化率大小,即曲线变化幅度的大小。
在补偿磨头有效切削半径之前,首先应确立一个合适的最大切削半径。如图8所示:曲线从有效切削半径1.2~1.5 mm处开始快速上升,说明其非球面轮廓度误差随有效切削半径变化的幅度逐渐增大。对非球面三坐标测量数据进行整理,可以得到刀具的有效切削半径为1.2、1.3、1.4、1.5和1.6 mm条件下的非球面轮廓度误差,如图9所示。
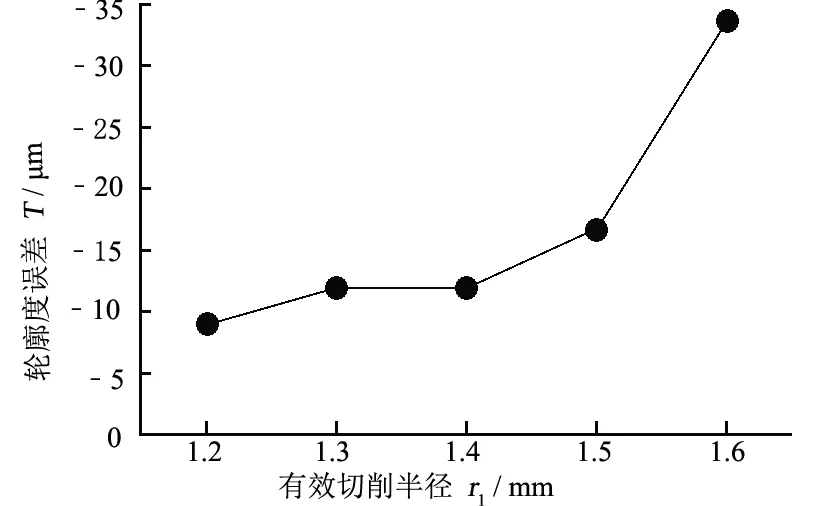
图9 不同有效切削半径下的非球面轮廓度误差
由图8和图9可以看出:当有效切削半径大于1.6 mm时,非球面轮廓度误差明显大幅度上升,同时非球面轮廓度误差随有效切削半径变化的幅度快速增大。因此,为减小非球面的轮廓度误差,磨头的最大有效切削半径宜控制在1.6 mm以下。
根据非球面轮廓度误差随铣磨刀具有效切削半径变化率的大小,相应确定铣磨刀具不同位置所对应的有效切削半径,建立以刀位点为原点,有效切削半径r1为横坐标,刀位h为纵坐标的坐标系,通过拟合得到优化设计的球磨头轮廓图10。图10给出了最大有效切削半径分别为1.2、1.3、1.4和1.5 mm时的球型磨头以及半径为3.0 mm的标准球型磨头轮廓曲线。
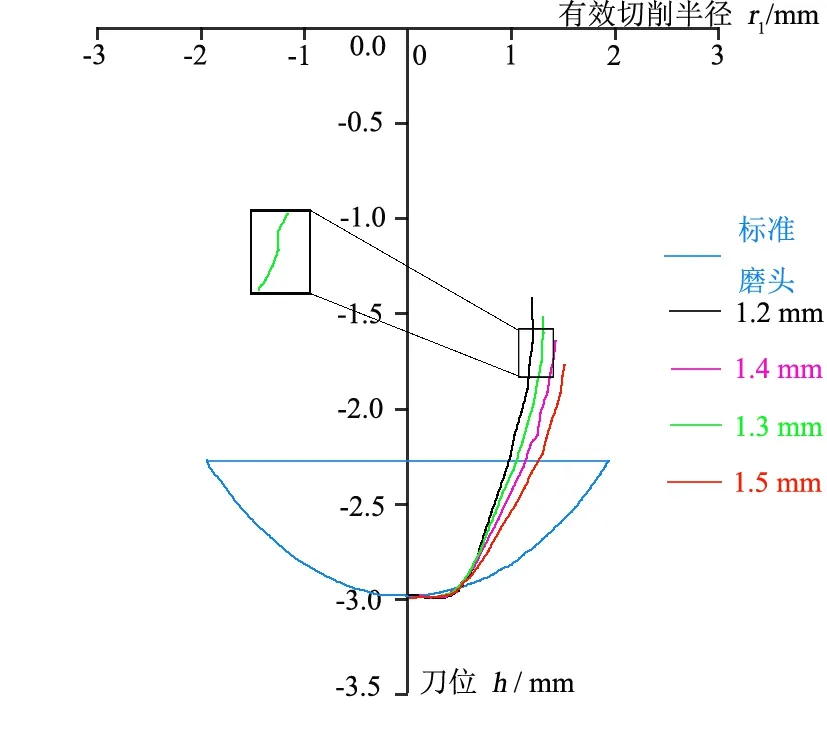
图10 不同有效切削半径的球磨头轮廓曲线
由图10可以看出:当最大有效切削半径小于1.5 mm时,刀具轮廓出现了向内凹陷的褶皱现象,如图10中的放大部分显示了最大有效切削半径1.3 mm时的球型磨头轮廓曲线褶皱部分,当刀触点在褶皱的凹陷处时,刀具对工件的切削由外切转变为内切,在加工时会出现过切现象。因此,磨头实际的最大有效切削半径最终考虑选择为1.5 mm,拟合的磨头轮廓曲线方程为:
(15)
3.4 非球面加工中磨头有效切削半径补偿实验
对铣磨刀具进行相应的有效半径补偿优化,制备最大有效切削半径为1.5 mm的金刚石磨头;使用优化的磨头、按表2的精磨工艺参数对半精磨加工后的非球面工件用平行精加工路径进行精加工,使用三坐标测量非球面的坐标点,并计算出非球面的轮廓度误差。
将实验测量数据整理可得:选用优化后最大切削半径为1.5 mm的金刚石磨头对K9光学玻璃进行非球面精加工,刀具路径选用平行精加工,用三坐标测量并计算得出玻璃加工后的最大轮廓度误差PV为44.52 μm,均方根RMS值为7.37 μm;而用半径3.0 mm的标准圆头金刚石磨头平行精加工K9光学玻璃非球面,其最大轮廓度偏差PV值为54 .48 μm,均方根RMS值为22.88 μm。因此,前者加工后的非球面面形精度较后者加工的精度显著改善,证明磨头有效半径补偿优化可以有效提高其加工面型精度。
4 结论
研究了轴对称非球面K9光学玻璃的铣磨补偿加工,用PowerMill软件控制三轴数控铣床,分别选用平行精加工和等高精加工2种刀具路径完成非球面的精加工,通过三坐标检测值计算求得非球面的法向轮廓度误差,得出如下结论:
(1)平行精加工路径和等高精加工路径的非球面最大轮廓度偏差PV分别为54.48 μm和98.46 μm,误差平均值RMS分别为22.88 μm和28.88 μm,即平行精加工条件下加工的非球面面型精度比等高精加工条件下加工的高;且随着加工过程中金刚石磨头与工件的接触点变化,非球面的轮廓度误差随非球面的高度呈现规律性的变化。
(2)对磨头轮廓度误差变化规律提出一种优化其有效切削半径的误差补偿方式。用优化后最大切削半径1.5 mm的磨头平行精加工K9光学玻璃非球面,其最大轮廓度误差PV为44.52 μm、均方根RMS值为7.37 μm,较切削半径3.0 mm的标准圆头磨头的平行精加工PV值54.48 μm下降了18.28%,RMS值22.88 μm下降了67.79%。因此,在三轴数控铣磨加工非球面过程中,选用有效切削半径补偿优化的磨头进行平行精加工轴对称非球面,可以有效减小其误差并提高其面型精度。
