非球面检测中最佳入射球面波和最佳参考球面波的确定
2012-10-30莫卫东贾晋超张海防冯明德杨百遇李均盛
莫卫东 ,范 琦,贾晋超,张海防,冯明德,杨百遇,李均盛
(空军工程大学 理学院,陕西 西安710051)
1 引 言
光学干涉及全息计算法是非球面光学元件面型检测的重要技术手段[1-6]。对非球面进行干涉检测时,需解决好两个关键问题: 其一,采用怎样的入射光波,使之与被测非球面反射后形成的波面函数更简单或更接近于被测非球面的面型函数;其二,采用怎样的参考光波,使之与被测非球面反射波干涉后形成的干涉条纹密度适中,以便准确记录干涉条纹。
非球面检测入射光波有两种,一种是平行光波,另一种是点光源形成的球面光波。由于采用平行光波入射时,该光波被非球面反射后不可能是球面波或接近于被测非球面的面型函数的反射波,因此,在非球面干涉检测系统中通常采用由点光源形成的球面波作为入射光波。特别是当点光源位于非球面的焦点时,反射波将可能是球面波或平面波。该反射球面波或平面波干涉与参考球面波或平面波干涉都可用于非球面面型的检测。但由于非球面的焦点位置通常不在检测光路的范围之内,使得非球面的检测变得比较困难。由于入射该球面波的点光源不能位于被测非球面的某个焦点上,根据其对称性,非球面检测入射球面波点光源的最佳位置只能位于非球面对称轴线上。若该点光源在某个位置上,能使被待测非球面反射后的反射波波面函数更接近于被测非球面面型函数,可把由该点光源发出的球面波称为非球面干涉检测的“最佳入射球面波”。
对于现代数字化干涉技术,CCD 是否能准确地记录干涉图像是实现非球面面型高精度检测的技术核心。为此,在非球面的干涉检测中,多选用球面波作为干涉参考光波来减小干涉条纹密度,并使之与被测非球面的反射波干涉条纹密度最小。这里把该参考球面波称为“最佳参考球面波”或“最佳干涉参考球面”。最佳参考球面波取决于发出该球面波的点光源相对于记录干涉条纹CCD 平面的位置,且满足与被测非球面反射波干涉的条纹密度最小的条件。只有确定了最佳参考球面波,方可明确CCD 的选型、光学器件与光路参数的选择以及深化干涉图的分析计算和对非球面检测系统的精度评价等。
为实现对非球面光学元件面型的高精度干涉检测,本文提出了新的确定最佳入射球面波波源和最佳参考球面波波源的方法。采用提出的研究理论和计算方法可全面分析任意非球面与考球面波干涉后的条纹密度分布以及非球面干涉检测调试中涉及的一些问题。
2 最佳入射球面波波源位置的确定
非球面干涉检测的入射球面波应位于被测非球面的中心轴线上,如图1 所示,其位于轴线上的位置,取决于从该位置发出的球面波经被测非球面反射后的波面函数是否最接近于被测非球面的面型函数。本研究的核心是如何判断点光源的某个位置是否满足上述条件,为此采用了不同以往的方法来确定“最佳入射球面波”,并获得了满足最佳入射球面波条件的被测非球面反射波最接近于被测非球面的面型函数。
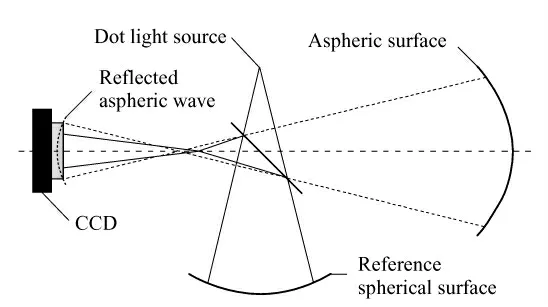
图1 数字全息检测非球面原理图Fig.1 Principle diagram of inspecting aspheric surface in digital holography
通过分析在被测非球面中心对称轴线上不同位置的点光源发出的球面波与最接近非球面面型函数的反射波( 分析计算时直接采用被测非球面的面型函数作为该反射波波面函数) 产生干涉的条纹密度,便可获得满足最佳入射球面波条件的点光源的位置。该干涉条纹的密度取决于球面波与被测非球面反射波之间的夹角,相当于文献[7]所提出的斜率非球面度。由于是球面波与非球面波的干涉,所以干涉条纹的密度是不均匀的。因此,不同位置的点光源发出的球面波与非球面反射波干涉的最大干涉条纹密度也不一样。当两者形成的干涉条纹的最大密度最小时,表明该球面波最接近于被测非球面反射波,该球面波的法线与该非球面反射波法线的最大夹角最小,该球面波就是被测非球面反射波的最接近比较球面。由于所取的非球面反射波为被测非球面的面型函数,因此,该位置点光源发出的球面波便是非球面干涉检测的最佳入射球面波。
确定最佳入射球面波波源位置rbest( 在对称轴上距被测非球面顶点的距离) 的具体计算方法,参照下面的“最佳参考球面波”的确定方法,其思路与算法完全相同。
3 最佳参考球面波波源位置的确定
3.1 在CCD 上记录干涉波的特点分析
如图2 所示,检测时需要记录的干涉图并不在非球面上,而是记录在某个平面M( CCD) 上。显然,在记录平面M 上所记录的干涉图并不是在非球面附近某个参考球面波与非球面产生的干涉,而是不同半径的参考球面波与被测非球面的反射波的干涉。在M( CCD) 上,被测非球面反射波与参考球面波的夹角随着参考球面波半径的改变,在非球面上的夹角也在不断改变。即非球面上某点的斜率非球面度在干涉图的记录平面M( CCD) 上并不相同,也就是说,在记录平面M( CCD) 上所记录的干涉条纹密度实际上不同于定义在某个参考球面波上的斜率非球面度估算的干涉条纹的密度。

图2 在M( CCD) 上的非球面和球面参考波Fig.2 Aspheric wave and reference spherical wave in M( CCD)
对于平面干涉仪来说,干涉图像记录平面M( CCD) 的位置不会影响干涉条纹的分布,而对于采用参考球面波的非球面干涉检测系统,干涉图记录平面M( CCD) 的位置直接影响着参考球面波与被测非球面反射波的夹角─干涉条纹的密度。可见,用于非球面检测目的的任何最接近比较球面,将不仅与非球面的面型函数以及口径大小等参数有关,还与干涉图的记录平面位置直接相关。因此,采用斜率非球面度确定最佳参考球面波以及用斜率非球面度评价非球面检测的难度可能有一定的局限性与偏差。
本研究试图通过直接计算干涉图记录平面CCD 上的参考球面波与被测非球面反射波的干涉条纹密度来确定非球面检测的最佳参考球面波。
3.2 干涉条纹密度计算的理论分析
如上所述,非球面反射波与非球面面型并非存在确定的数学变换关系。不同的入射波经非球面反射后的反射波会有很大的差异,有的反射波可能与面型具有相同或近似的描述函数,只是边界条件或某个常量不同; 而有的反射波可能与非球面面型函数差别很大,即二者是完全不同的两类函数。但对于非球面反射波波面与被测非球面面型,依据光路设计总能找到二者的对应关系,从而能够通过非球面的反射波反推得到被测非球面的面型信息。本研究选择的入射波为上述的最佳入射球面波,因此,在被测非球面表面的反射波最接近其面型函数。该反射波传播到CCD 时,可近似地按照CCD 的大小与被测非球面口径的比例“缩小”。以被测非球面的面型为二次旋转对称曲面为例,其反射波函数同样也为二次曲面:
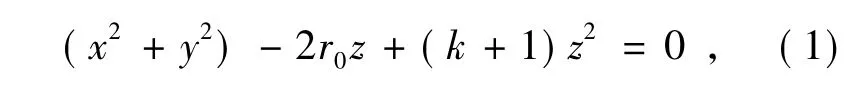
式中:z为旋转对称轴,曲面的顶点位于坐标原点O处;k为二次曲面系数,与被测非球面面型函数一致;r0为被测非球面反射波波面( 二次曲面)顶点的曲率半径,但r0并不是被测非球面面型函数顶点的曲率半径R0,通常r0需要事先根据检测光路结构参数以及被测非球面面型函数与反射波波面函数的关系计算得到。按照图1 的非球面检测方案,反射波顶点的曲率半径r0近似地按照反射波的口径φ( CCD 的尺寸) 与被测非球面的口径Φ 的比例缩小为:从式( 1) 中解出z:

取不同的k值代表不同的二次非球面。偏离二次曲面的非球面称为高次非球面,通常表示为:
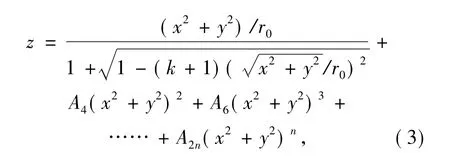
式中,A4,A6,……,A2n为高次非球面多项式系数。
考虑到非球面旋转对称性,以下非球面用x=0平面与非球面的交线─二次曲线或高次非圆曲线表示。式(3) 为:

记录干涉图的平面M( CCD) 可位于非球面反射波顶点前后任意位置,具体位置由两个因素决定:一是干涉图记录平面的有效面积( 如CCD的尺寸) ; 二是非球面光学镜片的有效口径。如图3 所示,假设记录干涉图平面M( CCD) 位于被测非球面反射波顶点的右侧,距原点的距离为b;S为参考球面波的波源位置,距原点的距离为a。
从S发出的球面波在记录平面M( CCD) 上各点的球面波半径并不相同。也就是说,在M( CCD) 上与非球面反射波干涉的球面波并不是相同的球面波波阵面,相对于半径为a的波面具有一定的位相差。可见,在CCD 上记录的是不同的参考球面波与非球面反射波的干涉结果,M( CCD) 上某点干涉波的强弱取决于非球面反射波与参考球面波在此点的相位差。

图3 非球面反射波与参考球面波的光程差Fig.3 Optical path difference between reflected aspheric wave and reference spherical wave
3.3 干涉条纹密度的计算方法
严格来说,非球面反射波与参考球面波在CCD 上的相位差等于二者从分束开始之后的光程差,由于二者行进的光路不同,精确计算难度很大。为此,采取了回避计算非球面反射波与参考球面波初相位差的策略,以非球面反射波顶点到达CCD 开始计时,同时到达的参考球面波Rc0也由此开始计时,相当于参考球面波与非球面反射波由此开始分束。这样,非球面反射波其他各点到达CCD 的Ci(yci,b) 处落后的光程为:

同时到达CCD 上Ci(yci,b) 点的参考球面波与开始计时的参考球面波面Rc0的光程差为δ2i:
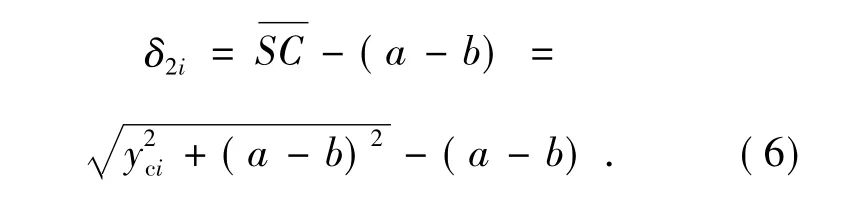
取CCD 短边的万分之一作为yci的取值间隔,约为CCD 信源尺寸的1/5。也就是说,数值计算可分辨的条纹宽度为CCD 信源的1/5。δ1i与δ2i之差便是所要求的非球面反射波与球面参考波在CCD 上的光程差δi=δ1i-δ2i。
但是,上述方法所计算的实际相位差缺少了二者之间的初相位差以及实际的光程差。对于非球面反射波与参考球面波干涉条纹来说,最大的误差也就是一个条纹位置,并不影响对干涉条纹密度的分析,可以看成是一次合理的近似。最终的计算分析结果证明了上述假设与近似的合理性。
当δi= ±jλ(j=1,2,3…) 时,非球面反射波与参考球面波干涉加强为亮条纹。按照一定的精度要求,检验每一个δi是否是波长的整数倍。那些是波长整数倍的点就是所求的干涉条纹的亮纹中心,相邻两亮纹中心的距离便是条纹宽度,由此可得到干涉图的最大条纹密度及其位置。
连续改变参考球面波波源的位置S(a,0) ,使a从0.5r0变化到1.5r0,变化步长取r0/100。计算每一个位置的参考球面波与被测非球面反射波在CCD 上干涉的最大条纹密度,由此得到不同参考球面波波源位置a与最大条纹密度的关系曲线( 见图4) 。在图4 曲线中,最大条纹密度的最小极值点所对应的参考球面波波源的位置a便是该非球面干涉检测最佳参考球面波波源的位置abest,即对非球面面型进行干涉检测时,使得最大条纹密度最小( 干涉条纹最疏) 的参考球面波波源的位置。由该点发出的球面波就是所要求的最佳参考球面波。
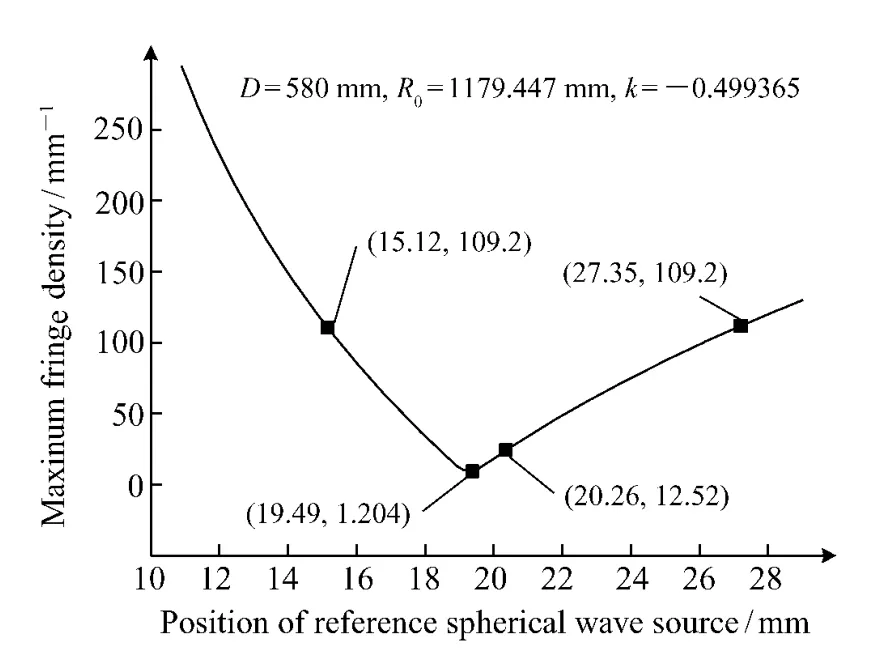
图4 最大条纹密度与参考球面波源位置的关系Fig.4 Relation between maximum fringe density and position of reference spherical wave source
3.4 计算结果及位置预判
表1 为按照上述理论分析和计算方法,针对图1所示的数字全息检测系统,对文献[7-10]中选用的二次非球面进行检测时所要求的最佳参考球面波波源位置以及最佳入射球面波位置的预判结果。

表1 不同非球面检测时的最佳入射球面波和最佳参考球面波的波源位置Tab.1 The best positions of incident spherical wave source and reference spherical wave source at testing of different aspheric surfaces
根据上述理论及方法可做进一步的应用研究。首先,当对某个非球面检测时,根据图4 参考球面波波源位置a与最大条纹密度的关系曲线,可知不同参考球面波在CCD 上与被测非球面反射波干涉条纹的最大密度,该干涉条纹最大密度便是选择CCD 分辨率的临界条件。即数字化干涉检测系统对非球面进行面型检测时,其CCD 的分辨率必须大于相应参考球面波与被测非球面反射波干涉的最大干涉条纹密度,否则,将不能满足干涉条纹采样精度要求。进而,根据所选择的CCD 最大尺寸,可确定检测光路中参考球面镜的参数等。
另外,从图4 曲线可发现,当参考球面波源的位置偏离abest约5%,干涉条纹密度将急剧增加10 倍,这足以说明在非球面检测前确定参考球面波波源位置的重要性。不过,进一步的分析发现,在目前所采用的CCD 分辨率条件下,参考球面波波源的位置冗余较大。以本研究所采用的CCD为例,其分辨率约为109 pixel/mm,根据图4 曲线可知,只要参考球面波源的位置不小于abest的20%(4 mm) 或大于abest的40%( 7.5 mm) ,均可做到非欠采样记录全息图。由图4 还可看到,当参考球面波源的位置a<abest时,条纹密度变化梯度相对于a>abest时要大。也就是说,调试时,从a<abest端开始调试更有利于找到最佳参考球面波波源的位置。
此外,本文还进一步做了一些与非球面干涉检测调试相关的分析研究。如: 在被测非球面口径一定的情况下,连续改变二次曲面系数k,分别预判了大、中、小口径的非球面的最佳球面参考波的位置与二次曲面系数k的关系以及与非球面反射波顶点曲率半径的关系等。研究发现: 当二次曲面系数的绝对值很小(<2) 的情况下,无论口径大小如何,最佳球面参考波的位置都与非球面反射波顶点曲率中心很接近,相差均不到1%,可以近似等于非球面反射波顶点曲率半径,即abest≈r0。而当二次曲面系数k不断增大时,最佳球面参考波的位置将远离非球面反射波顶点曲率中心(a>r0或a<r0) ,且最大条纹密度也将不断变大。同样,在二次曲面系数k很小的情况下,最佳入射球面波波源的位置将位于被测非球面面型函数顶点曲率中心R0附近。
4 结 论
本文从非球面干涉检测出发,提出了一种新的确定最佳入射球面波波源和最佳参考球面波波源位置的思路及方法。该方案采用直接计算干涉条纹密度的方法,分析球面波与非球面之间的相互关系,确定非球面检测时入射球面波波源的最佳位置和参考球面波波源的最佳位置。采用本研究提出的理论和计算方法,不需要任何解析计算便可全面分析任意非球面( 包括高次非球面) 与参考球面波干涉后的条纹密度分布,并可用于分析非球面干涉检测调试中可能遇到的诸多问题,为非球面的检测调试过程提供理论指导。因此,本研究对于实现非球面的数字化高精度快速检测具有重要的应用价值。
[1] 潘君骅.光学非球面的设计、加工与检验[M].苏州:苏州大学出版社,2004.PAN J H.The Design,Manufacture and Test of the Aspherical Optical Surfaces[M]. Suzhou: Suzhou University Press,2004.( in Chinese)
[2] 朱勇建,潘卫清.非球面面形测量技术[J].激光与光电子学进展,2010,47(1) :11202.ZHU Y J,PAN W Q. Measurement of aspheric surface[J].Laser Optoelectronics Progress,2010,47(1) :11202.( in Chinese)
[3] 席庆奎,朱日宏,陈磊,等.计算全息用于非球面检测的方法[J].激光杂志,2004,25(6) :67-69.XI Q K,ZHU R R,CHEN L,et al.. Methods on testing an aspheric with a computer generated hologram[J].Laser J.,2004,25(6) :67-69.( in Chinese)
[4] TAKAHASHI T,KONNO K,KAWAI M,et al.. Computer generated holograms for testing aspheric lenses[J].Appl.Opt.,1976,15(2) :546-549.
[5] 谢意,陈强,伍凡,等.用双计算全息图检测凹非球面[J].光学学报,2008,28(7) :1313-1317.XIE Y,CHEN Q,WU F,et al.. Concave aspherical surface testing with twin computer generated holograms[J].Acta Opt.Sinica,2008,28(7) :1313-1317.( in Chinese)
[6] 王虹,钱晓凡,庞永杰,等.一种离轴计算全息图在凹非球面检测中的应用[J].光学与光电技术,2011,9(1) :60-63.WANG H,QIAN X F,PANG Y J,et al.. Application of off-axis CGH to aspheric surface test[J].Optics&Optoelectronic Technology,2011,9(1) :60-63.( in Chinese)
[7] 谢枫,郝群,朱秋东.基于斜率非球面度的非球面最接近比较球面定义[J].光学学报,2010,30(11) :3197-3202.XIE F,HAO Q,ZHU Q D. Best-fit spheric surface definition based on slope asphericity for aspheric surface[J].Acta Opt. Sinica,2010,30(11) :3197-3202.( in Chinese)
[] 陆永贵,杨建东 光学非球面度的探讨[]长春理工大学学报, ,() :LU Y G,YANG J D. Discussing on the definition of optical asphericity[J].J. Changchun University Sci. Technol.,2005,28(4) :16-18.( in Chinese)
[9] 刘惠兰,沙定国,郝群,等.一种高次光学非球面度的计算方法[J].光电工程,2004,31(6) :44-47.LIU H L,SHA D G,HAO Q,et al.. A method for calculating asphericity of high order optical aspheric surface[J].Opto-Electronic Eng.,2004,31(6) :44-47.( in Chinese)
[10] 杜玉军,任海霞,刘中本.光学非球面元件非球面度计算方法[J].应用光学,2002,23(5) :42-45.DU Y J,REN H X,LIU ZH B. The method of calculation to asphericity of optical aspheric surface component[J].J. Appl. Opt.,2002,23(5) :42-45.( in Chinese)
