基于Simulink仿真的凸轮轴高速磨削稳定性判定*

罗德龙， 邓朝晖， 刘 涛， 佘帅龙， 罗程耀， 彭克立

(1. 湖南科技大学， 难加工材料高效精密加工湖南省重点实验室， 湖南 湘潭 411201) (2. 湖南科技大学 智能制造研究院， 湖南 湘潭 411201) (3. 湖大海捷(湖南)工程技术研究有限公司， 长沙 410012)

凸轮轴作为配气机构的关键零部件，其加工质量、精度等直接影响相关产品的使用性能和能耗标准[1]。近年来，高速磨削技术在凸轮轴加工中得到广泛应用[2]。作为典型的非圆轮廓零件，凸轮轴在高速磨削过程中的磨削力、磨削接触刚度等动力学参数均呈现出与普通外圆磨削和平面磨削不同的变化规律，给机床的动态性能带来极大挑战。

为提高凸轮轴磨削加工质量与精度，国内外学者在磨削颤振和工艺系统稳定性方面进行了诸多理论和实验研究，颤振分析理论体系已基本建立[3-8]。HAHN[4]首先提出再生型颤振的概念，认为加工表面的波纹再生是引起工艺系统振动的主要原因。ALTINTAS等[5]对纵磨再生颤振动力学模型进行了建模分析及表面波纹度研究。ZHANG等[6]通过切除材料的几何特征，建立了动态磨削力模型并分析了其与稳定性的关系。XU等[7]建立了外圆切入磨削非线性动力学模型。王龙山等[8]探讨了影响工件颤振频率的因素——工件接触刚度和砂轮的非线性刚度，通过实验和理论分析认为增大磨削力可以非线性提高其接触刚度；而且，增大磨削力还可以使工件系统的颤振频率提高。蒋永翔等[9]建立了外圆切入磨工件、砂轮再生颤振动力学模型及稳定性判定条件，并验证了该模型及稳定性理论的正确性。迟玉伦等[10]对外圆切入磨材料去除率模型的时间常数进行研究，提出了磨削接触刚度的有效测量方法，并建立其与系统固有频率的关系。

上述研究都停留在理论层面，离实际工程应用相距甚远，且多集中在平面或外圆磨削上[2]，而针对凸轮轴类非圆轮廓零件的磨削稳定性研究还不够深入，缺乏精准的动力学参数获取方法。因此，有必要针对凸轮轴高速磨削工艺系统稳定性问题开展研究，建立相应的磨削动力学模型，分析其稳定磨削区域，并基于Matlab/Simulink搭建磨削过程颤振仿真模型，选取适当的磨削工艺参数进行数值仿真分析与验证，以达到避免颤振、提高加工质量和效率的目的。

1 凸轮轴高速磨削系统动力学模型建立

1.1 磨削系统简化

一般认为磨床在切线方向(Y向)的整机动刚度足够大，引起动态切削厚度b(t)变化的主要原因是磨削力径向分力的波动。因此，磨削系统可以简化为如图1所示的单自由度系统。

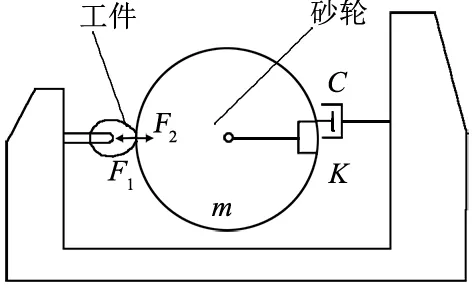
图1 凸轮轴高速磨削系统动力学模型 Fig. 1 Dynamic model of camshaft high speed grinding system

该磨削系统动力学模型的运动微分方程可表示为：

(1)

其中：Fn(t)为磨削过程法向动态磨削力，m为系统的等效质量，K为系统的等效刚度，C为系统的等效阻尼，并设X(t)为砂轮架系统的瞬时振动位移。

1.2 磨削过程参数求解

根据熊超等[11]建立的凸轮非圆轮廓法向磨削力Fn数学模型：

(2)

其中：k是与工件材料有关的磨削力系数；μ表示砂轮宽度或者被加工工件宽度；γ为砂轮磨粒的圆锥半顶角，一般取γ=60°；d0为平均磨粒间隔；ε为影响系数，且ε=0.2～0.5；ap为砂轮磨削深度；vw、vs分别表示磨削点线速度和砂轮线速度；ds为砂轮直径，dρ为凸轮上瞬时磨削点的曲率直径。

由式(2)可以看出：影响磨削过程中法向动态磨削力变化的主要因素有瞬时磨削深度ap、凸轮磨削点的线速度vw和磨削点曲率半径dρ等。由于本文凸轮轴磨削采用恒线速磨削加工方式，故动态磨削力的影响因素主要考虑瞬时磨削深度ap和当量砂轮直径de，当量砂轮直径的计算公式如下：

(3)

以某型号汽车凸轮轴为例，该凸轮基圆半径15.5 mm，砂轮半径200 mm，滚子测头半径8 mm，最大升程值为凸轮转角位于98°时的5.1525 mm，且凸轮两侧带有凹面。通过Matlab编程计算，得到凸轮曲率半径dρ与转角之间的对应关系，如图2所示。

图2 凸轮曲率半径与转角之间的对应关系 Fig. 2 The corresponding relationship between the Radius

根据文献[1]，可以求得任意磨削点p处工件的角速度ω，如公式(4)所示：

(4)

同时，根据转角与时间的函数关系式(5)，将凸轮转角视为中间变量，即可得到凸轮曲率半径与时间的对应关系，图3(凸轮基圆转速为nw=90 r/min)

(5)

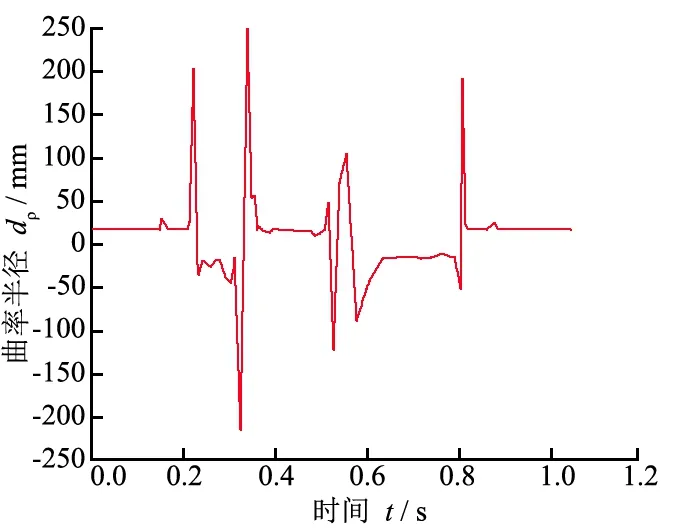
图3 曲率半径与时间的对应关系图 Fig. 3 The corresponding relationship between the radius of curvature and the time

根据文献[1]，对于任意时刻t，磨削系统的输入量为理论磨削深度；磨削系统的变量为砂轮磨损量、凸轮轴的去除量、砂轮与工件之间的接触变形以及磨床系统的结构变形(即系统振动的振幅)；磨削系统在任意时刻的理论磨削深度等于此时的砂轮磨损量和凸轮轴的去除量、砂轮与工件之间的接触变形、磨床系统的结构变形之和；磨削系统的输出量为动态磨削力。由于在凸轮轴高速磨削过程中，砂轮存在定期修整，如果忽略砂轮的磨损对动态磨削过程的影响，从而得到任意时刻t凸轮磨削的实际磨削深度(凸轮轴的去除量)计算公式：

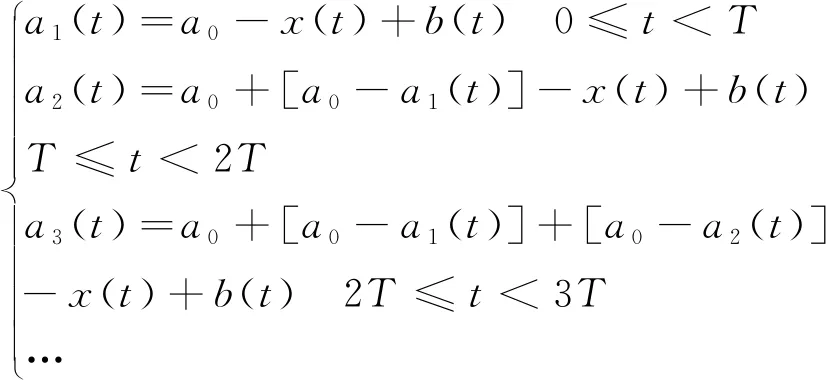
(6)

其中：a0表示凸轮磨削时单圈的理论磨削深度；ai(t)表示第i圈的实际瞬时磨削深度值；x(t)表示任意时刻t砂轮与工件之间的接触变形量；b(t)表示工件表面的动态振纹。b(t)为：

b(t)=b0-[X(t)-X(t-T)]

(7)

其中：b0表示凸轮表面的初始振纹，X(t)为工艺系统的瞬时振动位移，T为工件主轴的旋转周期。

从式(7)可以看出：凸轮轴高速磨削工艺系统是一个时滞非线振动系统。对于凸轮轴和砂轮之间的接触变形x，考虑工件经过了热处理以及局部冷激工艺，具有较高的硬度，而砂轮表面的磨粒则是结合在结合剂上的，其接触变形较凸轮的接触变形要大得多，所以在分析中可用砂轮的接触变形近似代替砂轮和工件之间的总变形。砂轮的接触变形函数表达式如下[8]：

(8)

其中：k1=2.23，e=0.706，x的单位是μm。

2 凸轮轴高速磨削过程仿真与结果分析

2.1 磨削颤振仿真模型

根据前文所建立的凸轮轴高速磨削系统动力学模型，基于Matlab/Simulink搭建磨削过程颤振仿真模型，考虑将整个仿真分为2个功能模块，一块主要是用于求解动力学模型所对应的振动微分方程，另一块则是用于求解动态磨削力的子模块。

对于微分方程求解，通常采用积分方式进行子结构建模，首先选择Continuous中的integrator模块表示微分方程的各阶积分；采用Commonly used Blocks中的Gain模块表示微分方程的各个系数；采用Math Operations中的Add运算模块将微分方程进行等式表达；采用Sinks中的Scope模块显示输出。

而对于动态磨削力的求解，由以上分析可知，主要求解瞬时磨削深度和当量砂轮直径的值。由瞬时磨削深度推导公式(6)，采用Sources中的Clock模块来表示模型仿真时间；采用Signal Routing中的Switch模块表示仿真的分支结构；采用Commonly used Blocks中的Constant输入模块表示凸轮轴磨削加工设定的理论磨削深度；采用Continuous中的Transport Delay模块表示凸轮轴磨削加工每一圈的时滞项；采用Math Operations中的Add运算模块对磨削深度值计算求解；采用User-Defined Functions中的Fcn模块表示磨削力与磨削深度之间的函数关系；同时，根据前文所述的凸轮轮廓曲率半径以及当量砂轮直径的计算方法，为了将Matlab工作区中计算得到的当量砂轮直径随时间的函数关系代入到Simulink仿真模型中，采用Sources中的From Workspace模块来读入工作区中的计算数据，并使用Math Operations中的Product模块表示动态磨削力的各个影响因素之间的乘积关系。基于Matlab/Simulink环境，搭建的磨削过程计算机仿真系统模型如图4所示。

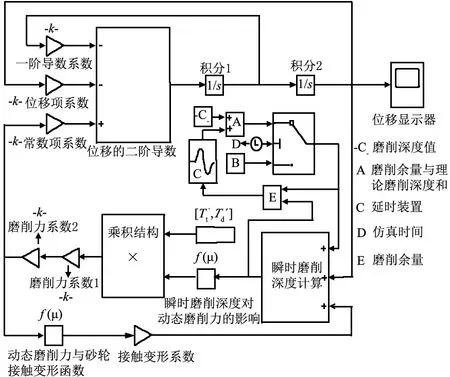
图4 凸轮轴高速磨削加工系统仿真框图 Fig. 4 Simulation diagram of camshaft high speed grinding

2.2 凸轮轴高速磨削过程仿真结果分析

根据前期对CNC8325B数控凸轮轴磨床进行的整机动刚度测试结果[12]：磨床整机X向(法向)动刚度为K=4.834×106N/m，系统的固有频率ωn=187 Hz，并由频率响应曲线用半功率法求得系统的阻尼比ξ=1.2%，由此可以求得磨削系统的等效质量、阻尼参数等。同时，磨削过程的其他仿真参数设置如下：凸轮宽度μ=25 mm，平均磨粒间隔d0=0.67 mm，影响系数ε=0.28，与工件有关的磨削力系数k=170 kg/mm，圆锥半顶角γ=60°。

仿真时，凸轮表面的初始振纹b0忽略不计，磨削过程的初始条件为X(0)=0、X′(0)=0。当砂轮线速度vs=120 m/s，工件基圆转速nw=90 r/min，理论磨削深度a0=0.02 mm时，凸轮轴高速磨削过程振动位移时域图如图5所示。

图5 凸轮轴高速磨削过程振动位移时域图 Fig. 5 The Time domain diagram of vibration displacement of camshaft high speed grinding

由图5可知：在上述磨削工艺参数下，工艺系统的颤振振幅最终趋于稳定，能够实现凸轮的稳定磨削。工件基圆转速nw=90 r/min时，通过Matlab求解得到单圈的磨削时间T=1.06 s。当凸轮从基圆上与桃尖相对的位置开始磨削前半圈，即图6所示凸轮轮廓的0°～180°范围时，在磨削开始阶段，由于磨削系统状态发生改变，产生剧烈的受迫振动，随后在系统阻尼的作用下振纹逐渐减小；而当磨削进行到凸轮升程段时，系统的振幅又有所增大，之后又继续减小，对应图5所示磨削第一圈的前半程。凸轮轮廓示意图如图6所示。

图6 凸轮轮廓

这一现象产生的原因可以从以下2个方面来分析：(1)由于凸轮升程两侧轮廓存在凹面，在磨削过程中引起动态磨削力的突变，因而振幅出现突变的现象；(2)在磨削凸轮升程段时，凸轮轮廓的曲率半径一般是先增大后减小，而由动态磨削力的计算公式(2)可知，动态磨削力与轮廓曲率半径之间存在正相关关系，因而系统的振幅也是先增大后减小。而当磨削过程从桃尖回到凸轮基圆的过程中，即图6所示的180°～360°范围内，系统的颤振振幅变化趋势与磨削凸轮前半圈时相似，都是先增大后减小，并且在回程段与基圆的连接处，由于凸轮轮廓凹面的影响，振幅同样存在突变现象，对应图5所示磨削第一圈的后半程。这与前期对凸轮轴磨削力的研究结果相一致。根据文献[13]，凸轮轴高速磨削动态磨削力的单圈采集实验结果如图7所示，其横坐标为凸轮轮廓上从0°～360°之间所布置的测点数，纵坐标为相应测点处所对应的磨削力。由图7可以看出磨削力随凸轮轮廓测点(也即转角)的关系基本上满足先增大后减小，再增大再减小的变化规律。

当凸轮磨削进行到第二圈时，由于前一圈磨削时工艺系统的振动以及砂轮的接触变形等使得磨削过程的实际磨削深度值小于理论磨削深度，从而在工件表面留下了动态振纹，根据瞬时磨削深度计算公式(6)及磨削力公式(2)可知，此时的动态磨削力发生突变，从而使得磨削系统的振幅急剧增大，对应图5中第一圈与第二圈之间交界部分系统振幅的突变现象。从图5中也能看出：其后的磨削过程系统的振幅变化趋势基本与第一圈类似，凸轮磨削各圈的振幅变化规律基本都是先增大后减小，再增大再减小。

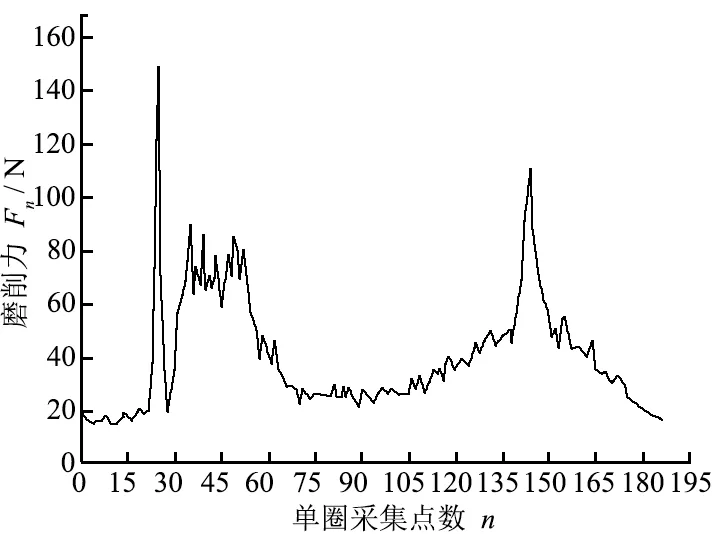
图7 法向磨削力单圈采集时域图 Fig. 7 Time domain diagram of single ring acquisition of grinding force

3 动态磨削仿真判定与叶瓣图判定

根据前期对凸轮轴高速磨削过程稳定性理论及研究结果分析[1]，得到磨削系统的稳定性叶瓣图如图8。

由图8可知：稳定性叶瓣图由一系列稳定性叶瓣构成，位于叶瓣下方的区域称为稳定磨削区，即图8中的蓝色部分；位于叶瓣上方的区域称为不稳定磨削区；而当磨削工艺参数刚好落在叶瓣线上时，此时的工艺系统处于临界稳定磨削状态，即系统本身是稳定的，但是如果给系统施加一个外部干扰，磨削系统则可能会从稳定状态过渡到磨削颤振状态。

图8 工艺系统稳定性叶瓣图 Fig. 8 The diagram of stability leaf flap of process system

在稳定性叶瓣图上选取几个比较有代表性的点，用这些点的磨削工艺参数组合对模型进行仿真验证。本研究选用的工艺参数组合如表1所示，表1中的实验号对应图8中相应点的编号，各磨削工艺参数对应的仿真结果分别如图9a～图9f所示。

由图9a、图9b可知：参数组合3、4下发生了磨削颤振，振幅值不断增大，但其振幅增长比较缓慢，对应叶瓣图中稳定磨削区与不稳定磨削区的临界区域；由图9c、图9d可知：参数组合5、6下振动逐渐趋于稳定，对应叶瓣图中的稳定磨削区域；由图9e、图9f可知：参数组合11、12下发生了磨削颤振，振动幅值不断增大，对应叶瓣图中的不稳定磨削区域。由此可知，基于动态磨削仿真的磨削稳定性判定与基于稳定性叶瓣图的磨削稳定性判定基本吻合，验证了本研究所建立的动力学模型及仿真方法的正确性。

表1 凸轮轴高速磨削仿真工艺参数表Tab. 1 The parameter table of camshaft high speed grinding simulation

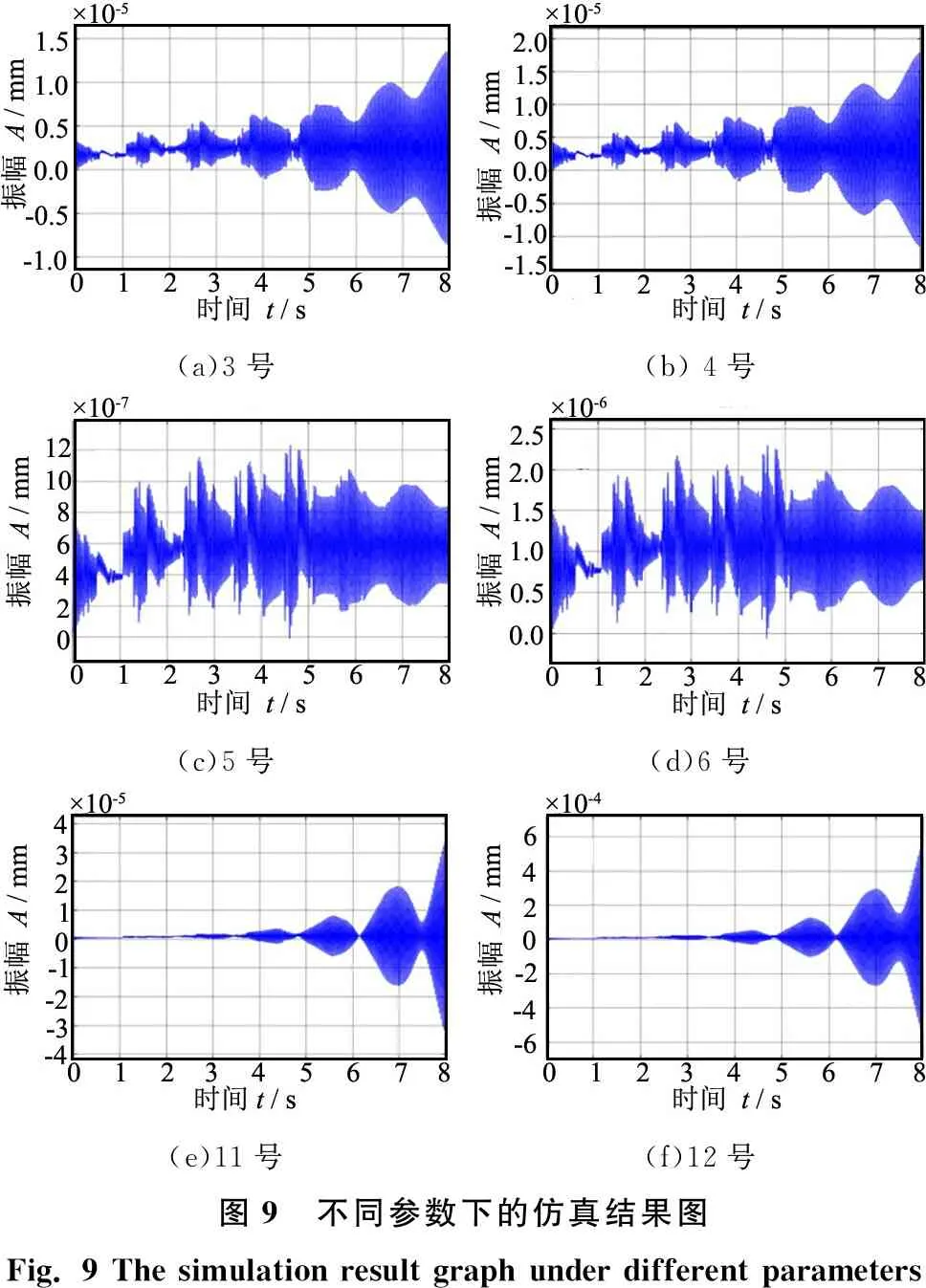
(a)3号(b) 4号(c)5号(d)6号(e)11号(f)12号图9 不同参数下的仿真结果图Fig. 9 The simulation result graph under different parameters

4 结论

以凸轮轴数控高速磨削过程为研究对象，分析磨削过程中的动态影响因素，建立磨削系统动力学模型，通过 Matlab/Simulink环境搭建了磨削过程的颤振仿真框图，基于凸轮轴高速磨削的稳定性分析结果，从稳定性叶瓣图上选取有代表性的点进行数值仿真分析，通过仿真所得振动位移时域图判定不同工艺参数组合下工艺系统的稳定性，并将仿真结果与稳定性叶瓣图所示的稳定磨削区域进行比较，验证了仿真模型的有效性，为凸轮轴的实际磨削加工工艺参数选择提供参考。