用问题激发思考，浅谈如何培养学生的问题意识

李俊

[摘  要] 数学是一门对于思考要求较高的学科，要想学好数学，学生需要经过深入而广泛的思考，要能将数学的思想方法和概念知识有机地融入自己的认知结构之中. 目前很多教师在进行数学教学时不能激发学生的思考，仅仅是将知识点呈现在学生的面前，这不符合学生的认知规律. 思考不是抽象的，它是问题导向的，教师要想能够调动起学生的思考，首先就是要培养学生的问题意识. 文章中，笔者就将分享自己对于培养学生问题意识的思考.

[关键词] 高中数学;问题意识

[?]前言

数学是一门集合了许多知识概念和思想方法的学科，要想学好数学，学生需要深入思考，以便能够将这些知识概念以及思想方法有机地构建成一种认知结构，然而，现在很多教师在展开具体的数学教学时，没有能够引导学生思考，仅仅是将这些要素呈现在了学生的面前. 显然，这样的教学方法不能满足教学要求，也不符合学生的认知规律. 如何有效地引导学生思考成为一个重要议题[1]. 纵观数学发展史我们不难发现，数学家们的思考从来不是空中楼阁，不是为了思考而进行的思考，他们的思考是问题导向的，是发现或者为了解决某一具体问题而逐渐深入和扩散的. 有一位著名科学家曾说过，发现问题也许比解决问题更加具有挑战性，也更重要，因为解决问题可能只是对现有知识的应用，而发现问题则需要人们从崭新的角度去审视原有的知识体系或者问题，需要一种思维的突破，也往往能够带来真正意义上的科学进步. 因此，引导学生思考这一目标可以转化为帮助学生养成正确的问题意识，即培养学生发现问题的能力和意识，这有利于学生的有效学习，也为学生的将来发展打下了基础.

[?]优秀的教学情境

笔者曾经前往A校听过一堂公开课，课堂的内容是推导三角函数的诱导公式，笔者认为该堂课的老师就处理得比较好，所以想在这里和各位读者分享一下当时的教学情境.

教学情境一：

教学目的：推导sinα，cosα与sin（α+2kπ），cos（α+2kπ）（k∈Z）之间的数量关系.

教学准备：教师利用多媒体展示器演示了如下动画：在平面直角坐标系中，有一个顶点在原点、始边与x轴正半轴重合的角α，现将其终边以顶点为原点作逆时针旋转.

教师设问：请同学们观察上面的动画，有没有发现哪些现象会重复出现？（为了引导学生深入思考，发现变化之中的问题，教师又提出了下面两个子问题）

子问题1：试在α的终边旋转的过程中取几个你认为比较特殊的位置，计算该处的三角函数值，试问：重复出现的现象对应的三角函数值之间有什么特殊的数量关系？如果想用数学表达式来描述，该如何书写？

子问题2：尝试结合动画，比较一下α和α+2kπ的三角函数值，能尝试解释一下这样数量关系背后的原因吗？

教学情境二：

教学目的：推导出sinα，cosα与sin（α+kπ），cos（α+kπ）（k∈Z）之间的数量关系.

教学准备：如果平面直角坐标系上还有另外一个角β，且已知将α的终边绕着原点逆时针旋转半周会与β的终边重合.

教师设问：不难发现，α和β之间存在奇妙的位置关系，那么这样的关系代表着什么呢？

子问题1：如果在该坐标系中加入一个单位圆，试问：这两个角与单位圆交点的坐标满足怎样的关系？

子问题2：结合上示图片尝试总结一下这两个角对应的三角函数值满足怎样的关系.

笔者认为，该教师在进行教学时不是简单地将知识点呈现在学生的面前，而是注意到了引导学生进行深入思考，教师将知识点包裹在一连串有层次、有梯度的问题中，让学生能够有自己逐步探索的空间，体现了对学生主体性的重视.

[?]从主观和客观两方面浅谈在数学教学过程中培养和提升学生问题意识的策略

1. 消除师生心理距离，营造良好的探讨氛围

现有的教学模式从本质上来说还是一种人际交往，教师与学生之间的关系很大程度上影响着学生的学习情况，良好和谐的师生关系能够让学生更加轻松和积极地投身于学习，疏离紧张的师生关系会在无形之中阻碍学生的发展. 同样的，对于培养学生的问题意识而言，师生关系和整体的学习氛围也发挥着不可忽视的作用，试想，如果学生不能对教师产生亲近信任的感觉，他们来找教师探讨问题，交流思考的主动性势必会下降. 教师应在平时的教学中保持平等温和的姿态，充分利用好学生天然的好奇心和探索欲，讓学生能够放开手脚，对问题进行个性化的思考. 对于学生的不同想法，教师应该保持一种包容的心态，不要急于否定，如果其中存在闪光点，教师也应该毫不吝惜地给出自己的表扬和称赞;对于学生思考中的不当之处，教师也不应该粗暴地批评，相反地，教师可以组织小组探讨活动，让学生通过合作探讨发现和解决问题. 总而言之，师生关系以及学习氛围这些看不到的主观因素会在一定程度上影响学生的积极性，教师应建设和谐的师生关系，营造开放包容的学习氛围，消除学生的心理距离，鼓励学生敢于表达新颖见解，引导学生敢提问、会提问[2].

2. 巧用多媒体技术，让学生在观察中发现问题

除了主观因素外，培养学生的问题意识还有一些客观因素需要考虑，由于数学学科本身的特性，有一部分知识对于学生来说会比较晦涩难懂，当面对较为复杂的问题时，学生往往会觉得无从下手，不知道该从何处入手分析，也就难以发现问题和提出问题了. 好在随着科学技术的发展，教师可以采用现代化的教学方法来将部分隐蔽晦涩的知识以生动的形式展现出来，这能够降低学生的接受难度，也能够让学生在更生动的演示中发现问题. 举例说明，在讲授圆锥曲线的统一定义一节时，教师就可以利用多媒体为学生们展示参数变化带来的图像类型变化，学生在学习这些知识的时候有时会遇到难以将参数和图像类型对应的问题，此时，这样的动态的展现方式就能很好地帮助学生将其对应起来，学生也会因此积极地去思考背后的原因.

3. 以错为引，引导学生在反思中提出新问题

学生在学习的过程中难免犯错，这很正常，这些错误之中也往往蕴含着学生知识体系或者理解上的缺陷之处，教师应利用好学生普遍性或具有代表性的错误，引导学生发现自己的不足，或是提出新的问题.

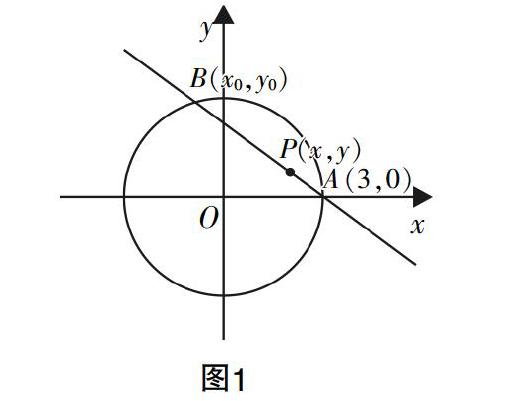
舉例说明，在复习课中笔者曾经给学生出过这么一道题：若平面直角坐标系中有一定圆M，现任取圆M上任意一定点A，过点A作圆的动弦AB，那么“该动弦中点的运动轨迹是椭圆”这一命题为真吗？绝大多数学生没有经过理论计算，仅凭自己的想象给出了肯定的答案，这暴露出学生还没有习惯用理论计算来得出答案的不良习惯. 对此，笔者没有急于否定，而是鼓励学生尝试说明理由，这个时候学生中出现了不一样的声音，有部分学生提出这个轨迹应该是圆，并表示通过圆的性质就可以证明. 笔者表示了肯定之后又抛出了一个问题：的确，动弦中点的运动轨迹是一个圆，那么是不是只有中点时这个结论才成立呢？随后，笔者让学生通过小组讨论的方式对这一问题进行了探讨，讨论结束后，笔者让学生们分享自己的想法，之后取了三等分点让学生尝试解决.

如图1所示，平面直角坐标系中有一个定圆O：x2+y2=9，取圆O与x轴正半轴的交点A（3，0），过点A作弦AB，取弦的三等分点P，试问：动点P的轨迹方程是什么？该轨迹方程表示的图形是什么？

在笔者的引导下，学生采用了向量法来解决该问题，具体的解决过程如下所示：设B（x0，y0），P（x，y），因为P是动弦的三等分点，A（3，0），所以（x0-3，y0）=3（x-3，y），所以x0-3=3（x-3），y0=3y. 又B是圆上一点，所以x+y=9，代入可知（x-2）2+y2=1，这就是P满足的轨迹方程，该轨迹方程表示的图形就是圆.

4. 类比知识，新生于旧

学生的学习是一个累积的过程，新知识与旧知识往往有着千丝万缕的关系，在教授新知识时，教师也可以带领学生回顾和对比旧知识，以此来激发学生的思考. 举例说明，学生在学习椭圆相关知识之前已经对圆较为熟悉，教师可以在教学过程中多进行对比，比如教师在讲授直线与椭圆相交弦长的相关知识时，可以先带学生回顾一下这段弦长在圆中有几个求法，学生在对比感悟的过程中往往能够产生一些新的想法.

参考文献：

[1]  张奠宙，张荫南. 新概念：用问题驱动的数学教学（续）[J]. 高等数学研究，2004（05）：10.

[2]  匡继昌. 如何理解和掌握数学概念的教学实践与研究[J]. 数学教育学报，2013（06）：74-78.