有效渗透数学文化的“数列的概念”的教学实践思考
2019-09-17李媛戴栋焱
李媛 戴栋焱

[摘 要] 站在数学文化的视角进行数学史的有效融入,结合学情进行数学教材的“二次开发”并重构教学方法,能使学生在思考与探究中经历、体验数学历史原貌并对知识形成深刻的理解以及获得数学新概念的感悟与构建.
[关键词] 数学文化;数学概念;有效;建构;数学素养
以数学学科与发展为背景、以数学课程与教学为载体所展现的文化是从物质形态角度对数学文化做出的解释. 着眼于数学知识形成过程中所蕴含的观点、信念、态度与方法所展现的文化是从意识形态角度对数学文化的理解. 学生经历、体验、感悟、欣赏数学活动的过程能够使其接受数学文化的感染与熏陶,数学课堂焕发生命活力的同时也会令学生的数学文化修养得以不断提升. 笔者就“数列的概念”这一内容对数学文化理念融入课堂做出了一定的思考.
[?]数学史激趣
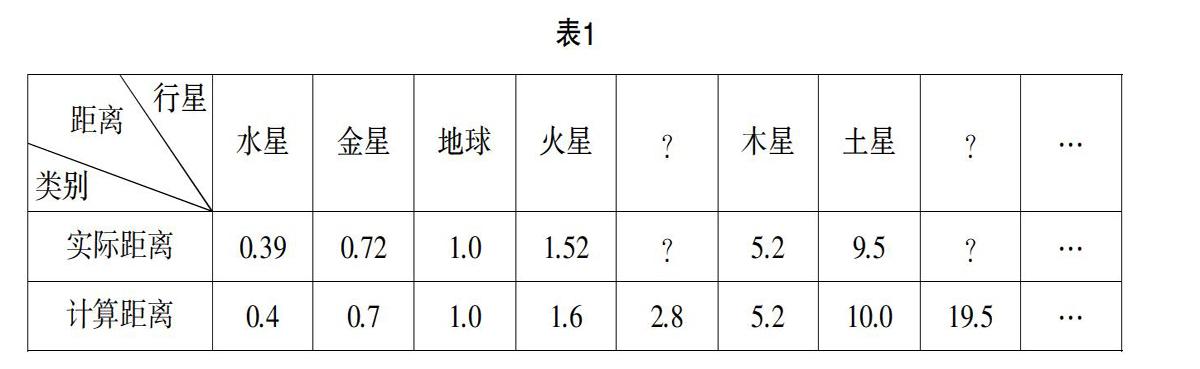
情境1:数列3,6,12,24,48,96,192, …,看起非常平常,德国天文学家提丢斯却运用这一数列进行了有趣的运算:在该组数据前加上“0”并因此得到“0,3,6,12, 24,48,96,192,…”,然后将数列中的每个数加上4并除以10,得到数列0.4,0.7,1.0, 1.6,2.8,5.2,10.0,19.6,…. 该数列中后数与前数之差组成了以下新的一列数:0.3,0.3,0.6,1.2,2.4,4.8,9.6,…,将这一列数与太阳到各行星之间的距离作比较可得表1中的结论(单位为天文单位).
提丢斯观察发现了第二组数和太阳距六大行星之间距离上的联系并预言了天王星的存在. 1781年发现的天王星也令提丢斯的猜想得到了证实,它与太阳之间19.2个天文单位的距离与19.6接近,人们也因此对提丢斯定则产生了信赖. 那么,从上表中的数据中,我们是否可以推断出在距太阳2.8个天文单位的区域内存在未可知的行星呢?天文学家们也因此在这一区域内进行了探寻. 1801年被发现的谷神星就是天文学家皮亚齐根据这一猜想而发现的. 宇宙运行的神秘面纱也因为这一神奇的一列数在世人面前得以揭开[1].
设计意图:科学史上的真实故事令学生对数列产生极大的兴趣,这是奠定学生数列学习情感基础的有效设计.
[?]数学史促思
情境2:古希腊毕达哥拉斯学派的数学家们喜欢在沙滩上进行数学研究,他们经常用小石子或画点的方法来表示数. 图1、图2就是他们研究过的三角形数(1,3,6,10,15,…)和正方形数(1,4,9, 16,25,…). 相继三角形数之和正好与正方形数相等,以此类推,可得相继正方形数之和与金字塔数相等(PPT展示数学家们的研究成果).
情境3:将“一尺之锤,日取其半,万世不竭”用数学的眼光进行解释即为:把“一尺之锤”视作1份并每天截去一半,剩下部分依次为1,,,,,,….
情境4:假如某细胞每小时分裂为2个,则该细胞每过1小时分裂的个数依次为1,2,4,8,16,….
情境5:某市2018年2月16日至20日的全天最低气温依次为1.1,-1.2,2.3,-0.4,-0.8. (单位:摄氏度)
设计意图:毕达哥拉斯学派崇尚的“万物皆数”理论以及数形结合的数学研究使学生更好地了解了数学的历史,数学知识生成的文化背景得以展露的同时,也令学生感受到了数学文化的熏陶以及数学研究的趣味性和文化性.
[?]辨析探究中建构概念
问题1:观察上述几组对象并说说它们的特点.
问题2:上述几组对象的语言描述在数的角度上来看可有共同特点?请表述.
设计意图:引导学生在观察、讨论、质疑和交流后对数列的概念进行归纳,使学生感受概念生成的自然.
问题3:1,2,4是数列吗?和数列4,2,1是同一数列吗?
问题4:之前我们学过的数学概念中,可有哪个概念和数列特别相像?它们是否一样?两者之间有区别吗?
设计意图:引导学生联想集合这已学知识并对两个概念进行辨析,使学生能够在辨析、比较中加深对数列概念的理解.
[?]类比探究中深化概念
问题5:指明数列中的项数即能确定其对应项,我们已学知识中可有与之密切相关的?
问题6:大家能用直觀方法对情境3、情境4中的数列进行表示吗?可有其他表示方法?
问题7:列表、图像、公式这三种表示法具备怎样的共同特征?涉及了哪些量?其间的关系怎样?
问题8:数列是不是函数?理由怎样?大家还记得函数有哪些要素吗?将数列{an}与函数类比,相当于函数自变量、因变量的分别什么?
设计意图:三种表示方法的共同特征是均能将项和序号之间的对应关系反映出来,数列中项的序号n和an之间的对应关系符合函数单值对应的特征,因此,数列是函数这一观点也就水到渠成了.
问题9:情境3中的数列可表示为an=
(n∈N*),即可建立关于序号n的函数. 以n为自变量的函数解析式f(n)即为数列{an}的通项公式,大家是否能够依此给出通项公式的定义呢?
设计意图:逐步揭示数列为函数这一实质并因此促进学生对数列概念本质的深层理解.
问题10:请大家观察图3所示的谢尔宾斯基三角形,观察白色小三角形的个数与数列的关系并写出一个通项公式.
问题11:若第一个等边三角形的面积是1,除去面积用白色三角形表示,那么上述4个三角形中黑色三角形的面积与周长分别是多少呢?如果面积与周长分别构成了数列{bn},{cn},大家能写出{bn},{cn}的一个通项公式吗?
问题12:观察数列{bn},{cn}的变化,并说说你有哪些结论.
设计意图:数学家谢尔宾斯基所创造的谢尔宾斯基三角形是非常美妙的数学发现,不断重复去除白色小三角形的过程能使黑色小三角的面积越发接近于零,周长则越发趋近于无穷大.
[?]反思中促进感悟和提升
1. 数学文化的融入能令学生的求知欲更加强烈
有效融入数学史料的课堂教学能令学生在数列概念的学习中充分感受到数学之美并获得启发. 提丢斯数列的引入使学生在课堂学习之初便感受到了数学的神奇,蕴含丰富数学文化元素的概念教学使课堂瞬间充满了浓厚的数学味道. 挖掘文化资源的情境设计又使学生对数列背后的文化意义建立了更好的了解并获得了数学思想、创新意识、理性精神的启发,数学思维与探究兴趣瞬间充斥着整个课堂[2].
2. 凸显数学文化的教学能更好地彰显概念本质
学生在认识数学知识时的历程实际上与数学文化的发展也有很多相似的地方,因此,数学学习的本质往往也能在数学文化的曲折发展中得以彰显. 教师应善于挖掘数学知识中的文化思想与现象并帮助学生领略其中所蕴含的数学思想、方法与观点,学生对数学概念的本质才会因此达成更好的理解与领悟.
3. 数学文化的融入能提升学生的数学素养
从侧面反映人类文化史的数学史对于人类文明史来说,也是特别重要的组成. 融入数学史料的课堂教学能更好地引导学生对数列问题进行选择、重组和加工,符合学生心理发展顺序的知识逻辑发展能使学生更好地结合已有知识展开思考与探究,如此情境的设计与学生的认知水平是吻合的. 比如,引导学生对情境2以及问题10~12的探究就是对学生数学文化的熏陶,學生接受文化洗礼的同时也能更好地感受数学的文化价值. 引导学生在数学史问题中的探究也是数学文化在课堂教学中的有效渗透与融入,学生的数学素养在教材的“二次开发”中也得到了更好的发展.
融入数学文化的课堂教学应有数学知识的传播到数学文化传播的转变,应能站在数学文化的视角进行数学史的有效融入,结合学情进行数学教材的“二次开发”并重构教学方法,能使数学知识的发生、发展过程与数学文化的有效融合. 因此,教师应善于挖掘数学知识背后的数学史料并以此为背景进行问题情境的创设,引导学生在问题链的思考与探究中经历、体验数学历史原貌并对知识形成深刻的理解,充分体会知识发生、发展与形成过程中所蕴含的思想方法并获得数学新概念的感悟与构建,令学生不断获得数学文化的熏陶并提升数学文化修养与素养.
参考文献:
[1] 王池富. 浅谈数学思维的诱导[J].数学教育学报,1995,4(1):52.
[2] 钱从新. 运用推广与引申的方法培养学生的创新能力[J]. 数学教育学报,2003,12(1):98.
