核心素养导向下统计与概率命题模式研究与解题策略研究
2019-09-10林元炳
林元炳
【关键词】 福建中考数学 数据分析 运算能力 数学阅读
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2019)22-059-02
“核心素养”是指学生应具备的适应终身发展和社会发展需要的必备品格和关键能力。数学学科核心素养是学生在接受相应学段的教育过程中,逐步形成的适应个人终身发展和社会发展需要的数学思维品质与关键能力。数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。《标准》将实验稿中的“统计观念”更名为“数据分析观念”,点明了统计的核心是数据分析。“数据分析观念”更加突出了统计与概率独特的思维方法:体会数据中蕴涵着信息;根据问题的背景选择合适的方法;通过数据分析体验随机性。
结合福建省近三年的中考数学所涉及的“概率与数据统计”问题,可以发现题目对于核心素养的考查有以下特点:
一、来源学生的生活实际,关注学生的情感体验,体现人文关怀
数学知识所具有的德育价值、心理价值和文化价值等内涵,是数学课程及其教学不可缺少的重要内容,是数学学科素养内在的必然要求。近三年的福建中考数学“统计与概率”试题都有出现贴近学生的学习生活或来源于学生熟悉的课本例题或练习题;学生通过答题,不但解决了问题而且启发了学生关心生活、关心社会、感受到统计与概率的应用价值;这类问题不但可以增强学生的答题信心,也培养了学生的统计与概率意识。
如:(2018·福建中考)第6题,投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )
A. 两枚骰子向上一面的点数之和大于1
B. 两枚骰子向上一面的点数之和等于1
C. 两枚骰子向上一面的点数之和大于12
D. 两枚骰子向上一面的点数之和等于12
本题来自课本例题,是学生非常熟悉的问题。这种类型的问题在2017年与2019年福建中考数学试卷均有出现过。试题让学生充分利用有关统计知识,来分析解决日常生活中的数学问题,培养学生的应用意识,同时又赋予试题的人文内涵。
二、利用图表提供数据,通过数据进行数学推理
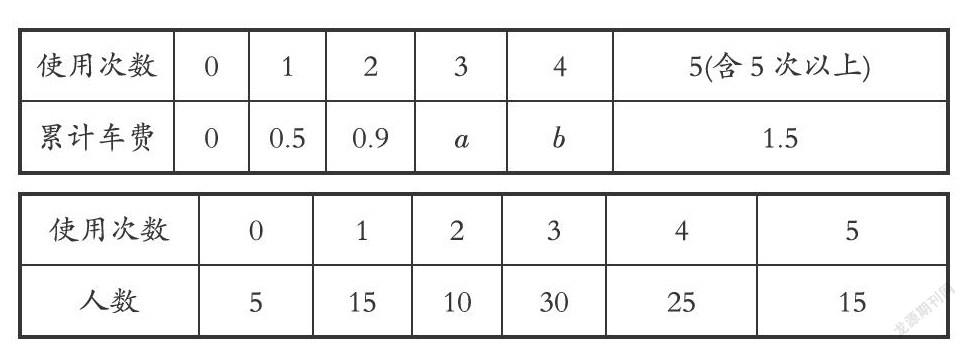
如:(2017·福建中考)第23题,自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费。具体收费标准如下:
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
(Ⅰ)写出a,b的值;[来源:Z。xx。k.Com]
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由。
史宁中教授说:“统计的核心是通过数据进行推理。”
本题通过题目中所提供共享单车的“使用次数与累计车费”以及“使用次数与人数”两个表格,要求学生从表格所提供的数据中找出“使用次数与累计车费”的线性关系,使用1次、2次……不同的次数车费的不同,再结合“一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.”这一描述;通过对表格的数据推理,让数据说话,从数据中提炼信息是这个问题的特征。学生通过问题的分析,一方面可以体会到数据整理的多样性,另一方面可以从表格中获取数据所蕴涵的信息;理清数据之间的联系,再进一步对信息进行加工处理,挖掘数据背后的信息,从而达到解决问题的目的。
三、加强了对学生数学运算能力的考查力度
数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的过程。主要包括:理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等。只有在掌握了运算方法的基础上,加强数学运算的训练和检测,才能够提高数学运算的速度和准确性;通过一定的强化检测,让学生明白算什么、怎样算、选择怎样的运算策略问题以及是否涉及分类讨论等等;使学生在练的基础上悟出运算的诀窍,达到熟能生巧的地步,从而提升运算能力,达到培养学生运算素养的目的。
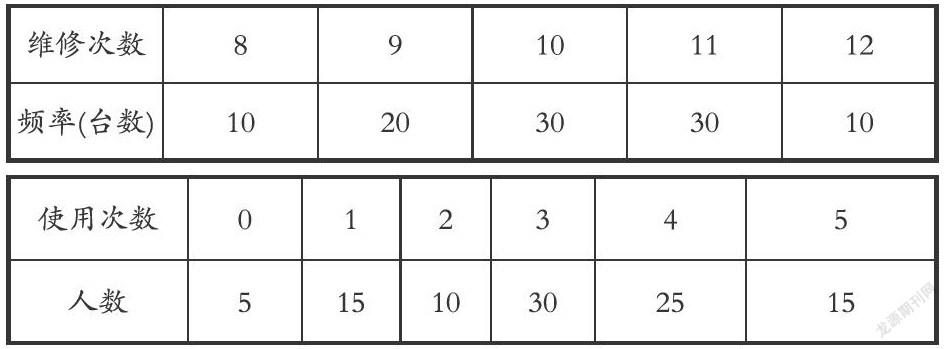
如:(2019·福建中考)第23题,某种机器使用期为三年,买方在购进机器时,可以给各台机器分别一次性额外购买若干次维修服务,每次维修服务费为2000元.每台机器在使用期间,如果维修次数未超过购机时购买的维修服务次数,每次实际维修时还需向维修人员支付工时费500元;如果维修次数超过购机时购买的维修服务次数,超出部分每次维修时需支付维修服务费5000元,但无需支付工时费某公司计划购实1台该种机器,为决策在购买机器时应同时一次性额外购买几次维修服务,搜集并整理了100台这种机器在三年使用期内的维修次数,整理得下表;
(1)以这100台机器为样本,估计“1台机器在三年使用期内维修次数不大于10”的概率;
(2)试以这100机器维修费用的平均数作为决策依据,说明购买1台该机器的同时应一次性额外购10次还是11次维修服务?
本题的解决要求学生要有扎实的运算能力,在厘清表格中维修次数与维修台数的对应关系的同时,要懂得运用加权平均数,结合分类讨论思想分别计算10次维修服务与此同时11次维修服务所需要的维修费用,以提供最优化方案决策。
同样,2017年福建中考数学第23题的“共享单车投放问题”、2018·福建中考数学第22题的“甲、乙两家快递公司揽件员日工资方案”问题均考查了对学生的“数学运算”,要求考生有良好的数学运算能力和运算水平。
四、对学生的数学阅读理解能力有较高的要求,需要精看细读,才能有效解题
数学是一门具有精确严谨思维形式的学科,其内容的展开以概念、公式、法则为基础,以严密的逻辑推理为线索,学生在进行阅读时要随着文本思维展开自己的思维,把阅读交流内容转化为自己易于接受的语言形式。数学阅读是学生个体根据已有的知识经验,通过阅读数学材料建构数学意义和方法的学习活动,是学生主动获取信息,汲取知识,发展数学思维,学习数学语言的重要途径。数学阅读是指围绕数学问题或相关材料,以数学思维为基础和纽带,用数学的方法、观念来认识、理解、吸取知识和感受数学文化的学习活动。?重视阅读理解能力培养,加强分析图表,从图表中获取正确信息的能力。
近三年的“统计与概率”试题大题字数分别为:2017年350字,2018年346字,2019年367字;所以要解决这三道题必需要有高深的阅读能力,认真阅读,理解题目中所提供的信息。运用样本估计总体思想,通过计算进行方案决策,体现了数学应用于生活的理念。
“大数据”时代,数据分析能有效地帮助我们发现规律、解决问题,所以培养学生的“统计与概率“意识显得尤为重要。要想培养统计能力,需要先有統计意识。“统计与概率”试题大题的考查方向使考生必需学会用数据说话,进而培养学生的理性精神和统计意识,也为教师们在平时的教学内容上指引方向。
全国教育科学“十三五”规划2017年度教育部重点课题《核心素养视角下的中考数学命题模式研究》(批准号DHA170351)成果。
[ 参 考 文 献 ]
[1]《义务教育数学课程标准》(2011年版).
[2]2016—2018福建中考数学试卷.
[3]《中小学数学阅读教学实验研究丛书·新课程中学数学阅读教学新论》四川大学出版社,2006年10月.
[4]章光虎.《教育学》2018年8月总第150期.
