基于SV模型的行程时间预测
2019-09-10杨超胡尧商明菊李扬周江娥
杨超 胡尧 商明菊 李扬 周江娥


摘要:行程时间的波动性分析及预测是道路交通网络研究的重要内容,为有效预测出行者行程时间,本文基于实际路段行程时间数据构建随机波动率模型,利用马尔科夫链蒙特卡洛方法求解模型参数,使用标准随机波动率(SV-N)模型和厚尾随机波动率(SV-T)模型对行程时间进行预测。结果表明:在刻画对路段行程时间波动率特征的效果上,厚尾隨机波动率模型优于标准随机波动率模型:在行程时间预测上,厚尾随机波动率模型更能准确地进行实时预测。本文方法对行程时间预测具有实时性,可对实际路段行程时间进行在线预测及对交通出行者的路线规划提供理论依据。
关键词:行程时间:SV模型:MCMC;波动性
中图分类号:0212文献标识码:A
行程时间是交通规划、运营和能力评估的重要指标。为了实现对车辆进行实时管控和疏导,行程时间必须进行实时预测,且要有较高精度。由于受到车流量与行人随机性变化及道路其它不可控因素的影响,导致出行者行程时间的变化具有时变、无规律和随机的特性,且呈现出较为复杂的波动特征。
目前,在道路行程时间短时预测研究中,国内外学者也提出了较多可靠的分析方法,主要包括随机漫步法、线性回归、神经网络、时间序列、模糊逻辑模型和支持向量机等。随机波动率(StochasticVolatility,SV)模型在1986年被提出以来,人们在对金融数据的处理上建立了大量的模型来拟合分析数据,从而做出合理的预测和估计,其中SV模型就是大量被采用的一种金融模型,它具有数理金融学和金融计量经济学的双重根源。然而由SV模型含有潜在变量,致使其似然函数极为复杂,求解其估计较困难。为解决这一问题:2002年,JAC-QULER等将贝叶斯理论与SV模型相结合,首次使用马尔科夫链蒙特卡洛(Markov Chain MonteCarlo,MCMC)方法估计,发现其估计效果比似然方法更有效:同年,TSE等实证分析了MCMC估计SV模型的效果,得出在SV模型参数估计方法中MCMC要优于伪似然估计等方法:陈杨林等用MCMC方法求解SV模型对黄金价格指数数据的未来趋势与变化进行了研究,且验证了该模型能够较准确地拟合黄金价格的未来变化趋势和较好地进行预测。而在交通领域中,应用SV模型分析数据较少。其中,李玮峰等应用SV模型对行程时间波动性进行分析,并说明了经济学对分析时间序列特征的模型中,在对道路行程时间波动率的解释上也有很好的可行性。因此,本文通过构建Sv模型对路段行程时间进行波动性分析,进而能够揭示行程时间波动结构的特征,对探究出行者行程时间的预测具有现实意义。
2实证分析
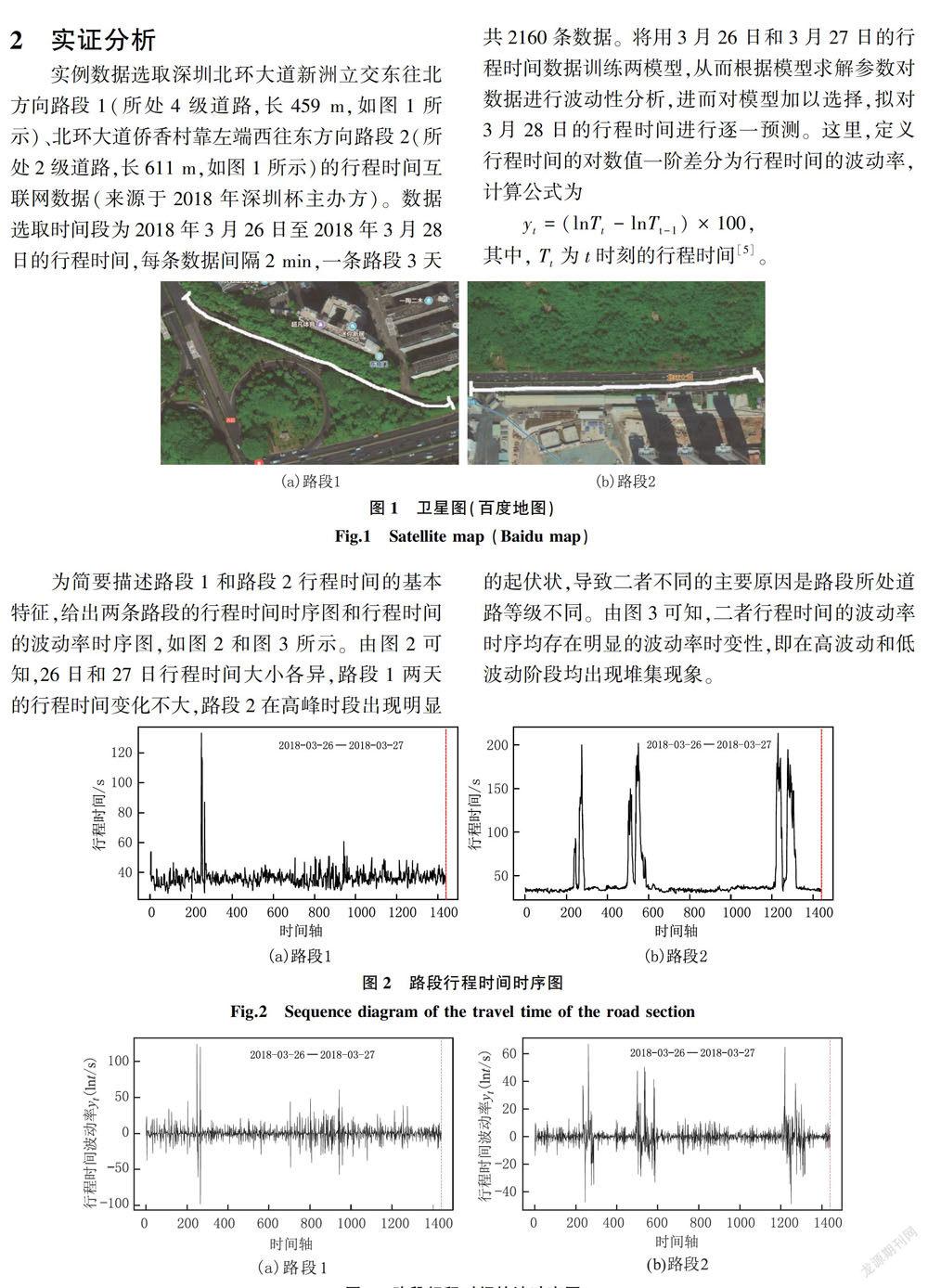
实例数据选取深圳北环大道新洲立交东往北方向路段1(所处4级道路,长459m,如图1所示)、北环大道侨香村靠左端西往东方向路段2(所处2级道路,长611m,如图1所示)的行程时间互联网数据(来源于2018年深圳杯主办方)。数据选取时间段为2018年3月26日至2018年3月28日的行程时间,每条数据间隔2min,一条路段3天共2160条数据。将用3月26日和3月27日的行程时间数据训练两模型,从而根据模型求解参数对数据进行波动性分析,进而对模型加以选择,拟对3月28日的行程时间进行逐一预测。这里,定义行程时间的对数值一阶差分为行程时间的波动率,计算公式为
y=(lnT—lnT)×100.其中,T为t时刻的行程时间。
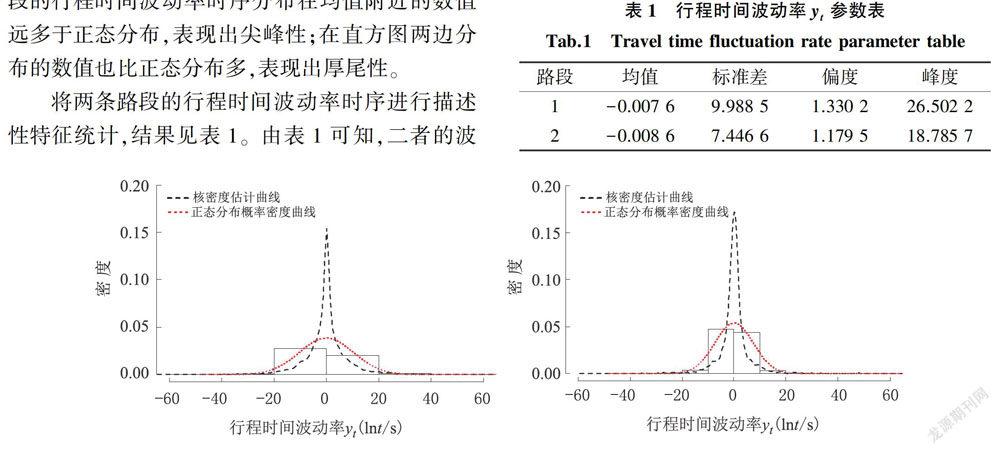
为简要描述路段1和路段2行程时间的基本特征,给出两条路段的行程时间时序图和行程时间的波动率时序图,如图2和图3所示。由图2可知,26日和27日行程时间大小各异,路段1两天的行程时间变化不大,路段2在高峰时段出现明显的起伏状,导致二者不同的主要原因是路段所处道路等级不同。由图3可知,二者行程时间的波动率时序均存在明显的波动率时变性,即在高波动和低波动阶段均出现堆集现象。
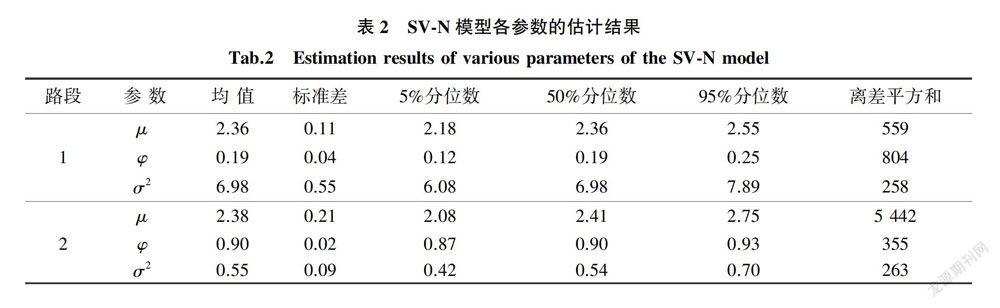
基于实例中的行程时间,利用频率分布直方图估计行程时间波动率核密度曲线,分析数据的基本特征,结果如图4所示。由图4可以看出,两条路段的行程时间波动率时序分布在均值附近的数值远多于正态分布,表现出尖峰性:在直方图两边分布的数值也比正态分布多,表现出厚尾性。
将两条路段的行程时间波动率时序进行描述性特征统计,结果见表1。由表1可知,二者的波动率时序数据均集中于均值附近:路段1和路段2的峰度分别为26.50、18.79.都大于3.再一次体现了二者的尖峰厚尾特征。
2.1SV-N模型的MCMC估计
路段1、路段2的SV-N模型各参数估计结果见表2。表2中,路段1的波动水平参数μ的估计值为2.36.而路段2为2.38.路段1波动水平参数的绝对值小于路段2.说明路段1的行程时间波动程度小于路段2。从波动持续性参数ψ角度分析,路段1为0.19.路段2为0.90.二者都小于1.表明二者均平稳且有较强的波动持续性,但相对路段1.路段2比路段1具有更强的波动持续性。从波动扰动水平υ上比较,由6.98远大于0.55.说明路段1行程时间波动的扰动水平比路段2高。
2.2SV-T模型的MCMC估计
路段1、路段2的SV-T模型各参数的估计结果见表3。表3中,路段1、路段2的波动水平参数υ的估计值分别为2.37、2.41.与路段2相比,路段1波动水平参数的绝对值较小,说明路段1的行程时间波动性较低,这与SV-N模型分析结果一致。从波动持续性参数ψ角度分析,路段1为0.19.路段2为0.91.二者均小于1.同SV-N模型一样,说明了两路段均平稳且有较强的波动持续性,并且路段2的波动持续性更长。从波动扰动水平υ上比较,由6.55远大于0.46.同样说明了路段1波动率扰动水平比路段2高。从模型自由度ω的估计看,路段1为33.32.路段2为30.67.再次说明两路段波动率分布非正态。
2.3模型选择
结合表2(SV-N)、表3(SV-T)中的模型参数的估计结果,从单条路段分析,对比SV-N模型和SV-T模型擬合实例数据的效果。对于波动水平μ的估计值来说,无论是路段1还是路段2.其绝对值均表现为SV-T模型的估计值更大,说明路段1、路段2在SV-T模型下表现出来的波动性均强于SV-N模型。就可持续性参数ψ的估计值而言,SV-N模型的ψ的估计值在0.20左右,SV-T模型的ψ的估计值在0.90偏上,说明路段2比路段1更具有波动聚集性效应;从整体上来看,SV-T模型中ψ的估计值比SV-T模型的大,说明SV-T模型比SV-T模型能更好地刻画两路段波动率的波动持续性。特别地,对于评价扰动水平的参数υ来说,当可持续性参数ψ越大,而υ越小时,波动的过程越易预测。在表2和表3中,SV-T模型的υ值均小于对应的SV-T模型中的值,说明SV-T模型的拟合效果优于SV-T模型。
基于前述分析基础上,利用两路段在SV-T模型和SV-T模型标准化残差的行程时间波动率Q-Q图来直观验证二者的优劣,如图5所示。从图5可以看出,和SV-T模型拟合的标准化残差基本都落在y=x直线上,相对SV-T模型而言,两路段在SV-T模型拟合下效果更好。
2.4行程时间预测结果
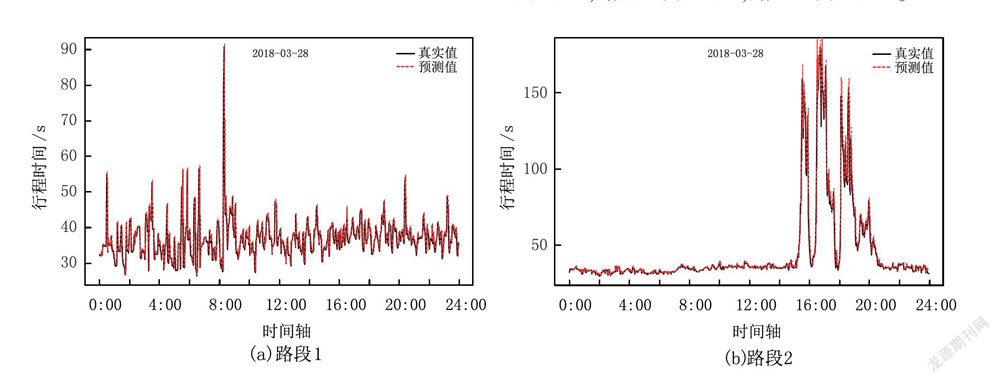
由以上对路段1、路段2的波动性分析可知,SV,T模型更能描述路段1、路段2的行程时间波动性。图6为基于SV-T模型对路段1和路段2的行程时间(3月28日)预测结果。图6可以看出,SV-T模型的预测效果非常好,这里计算了各路段实际值与值的MSE,路段1为22.68.路段2为70.04。
3结论
本文选取北环大道所处不同道路等级的两条路段26日和27日行程时间数据,分别构建SV-T模型、SV-T模型,并利用MCMC方法求解模型参数,对比模型拟合效果。结果表明:两条路段的行程时间均呈现尖峰厚尾特性:波动水平参数显示,道路等级较高的行程时间波动度显著,同时道路等级较高的波动持续性更强:从扰动波动水平角度看,道路等级低的相对较高。经实例分析证实,在刻画波动率的波动特征效果上,SV-T模型优于SV,N模型。选用SV-T模型对3月28日全天的行程时间进行逐一预测,两条路段预测效果较为精确。
