新增车辆通行拥堵预测模型

李扬 胡尧 商明菊 杨超 周江娥

摘要：为对新增车辆的通行拥堵进行预测，首先使用K-Medoids聚类算法将交通流运行状态划分为顺畅、阻滞、拥堵三类，然后引入交通流特征参数构建累积Logistic回归模型量化新增车辆对路段运行状态的影响，最后基于支持向量回归机预测新增车辆通行时间。研究结果表明：当只考虑车流量、限行时段和二者之间的交互作用时，模型预测道路状态的正确率达到82.36%，此时车流量在非限行时段每增加一辆车，发生比从顺畅状态转为非顺畅状态的概率是原来的1.087倍：当考虑车流量、黄牌车比例、限行时段、外地车比例及后两者的交互作用时，模型预测通行时间MSE最小，预测效果最优。

关键词：交通流运行状态;累积Logistic回归模型;支持向量回归机;通行时间

中图分类号：0212文献标识码：A

目前，世界各大中城市几乎都面临着交通拥堵问题。交通拥堵给人们的生活带来很多负面影响，例如降低人们的出行效率，对社会造成经济损失以及拥堵时尾气排放等问题。交通拥堵在很大程度上阻碍一个城市的发展，因此构建合理且易于实施的拥堵预测模型对人们尤为重要。

关于构建交通拥堵预测模型，有很多学者进行了研究。熊励等构建基于MapReduce的多元对数线性回归拥堵预测模型，预测效果良好：崔承颖等运用累积Logistic回归方法对各路段的拥堵概率进行估计：刘梦涵等将似然比方法和累积Lo-gistic回归模型结合运用到交通拥堵评价模型中。近年来，机器学习和深度学习也被广泛应用在交通拥堵预测上，然而大多数预测仅限于对当前的车流量状态进行预测，而根据当前的交通流状态，进行新增车辆通行拥堵预测的问题研究较少。

本文选取深圳市交通数据进行分析，运用聚类方法对交通状态进行划分，建立累积Logistic回归模型，分析新增车辆对交通运行状态的影响，并将构建的累积Logistic回归模型与支持向量回归机模型结合预测出新增车辆的通行时间。

1 模型理论

2实证分析

2.1数据准备

研究数据来源于深圳尚龙数学中心网站（http：//m2et，org/）公布的深圳市交通数据。选择的路段位于北环大道新洲立交西往东方向，长度575m，离其最近的卡口为10100206卡口，选择该路段2018年3月26日至2叭8年3月28日的数据，整理数据得出在该时段1～3车道的车流量（每两分钟过车数）、外地车（非粤B）汇人比和黄牌车（大车包括公交车）比例;此外，将白天设为1.黑夜设为0.将限行时段（7：00-9：00.17：30-19：30）设为1.非限行时段设为0.总结出时间属性：计算路段的路段通行时间（长度除以通行速度），上述数据粒度为2min（全天共有720个时刻，3天2160个时刻）。表1为整理后的该路段部分数据。

取2018年3月26日和3月27日的数据作为训练集，3月28日的数据作为测试集，得到卡口这3天每两分钟的过车数和通行时间时序图，如图1所示。

从图1可看出：3月26日和3月27日的过车数时序图趋势相差不多，而3月28日的过车数趋势在早上大约10点后下降，与实际情况相差较大，可能是数据的质量造成的：3月26日为星期一，其通行时间的早高峰（约8：00）较3月27日和3月28日明显，与实际情况相符。

2.2模型求解与评价

2.2.1基于Logistic回归的交通运行状态评估

将训练集（3月26日和3月27日）的车流量和通行时间（长度/通行速度）进行K-Meclioids聚类，得到3类交通运行状态聚类结果，设为1（顺畅），2（阻滞），3（拥堵）。根据聚类结果，结合滑动窗口构建解释变量集，将交通状态（顺畅，阻滞，拥堵）作为响应变量建立累积Logistic回归模型，经过多种模型的选择，得到三个模型。

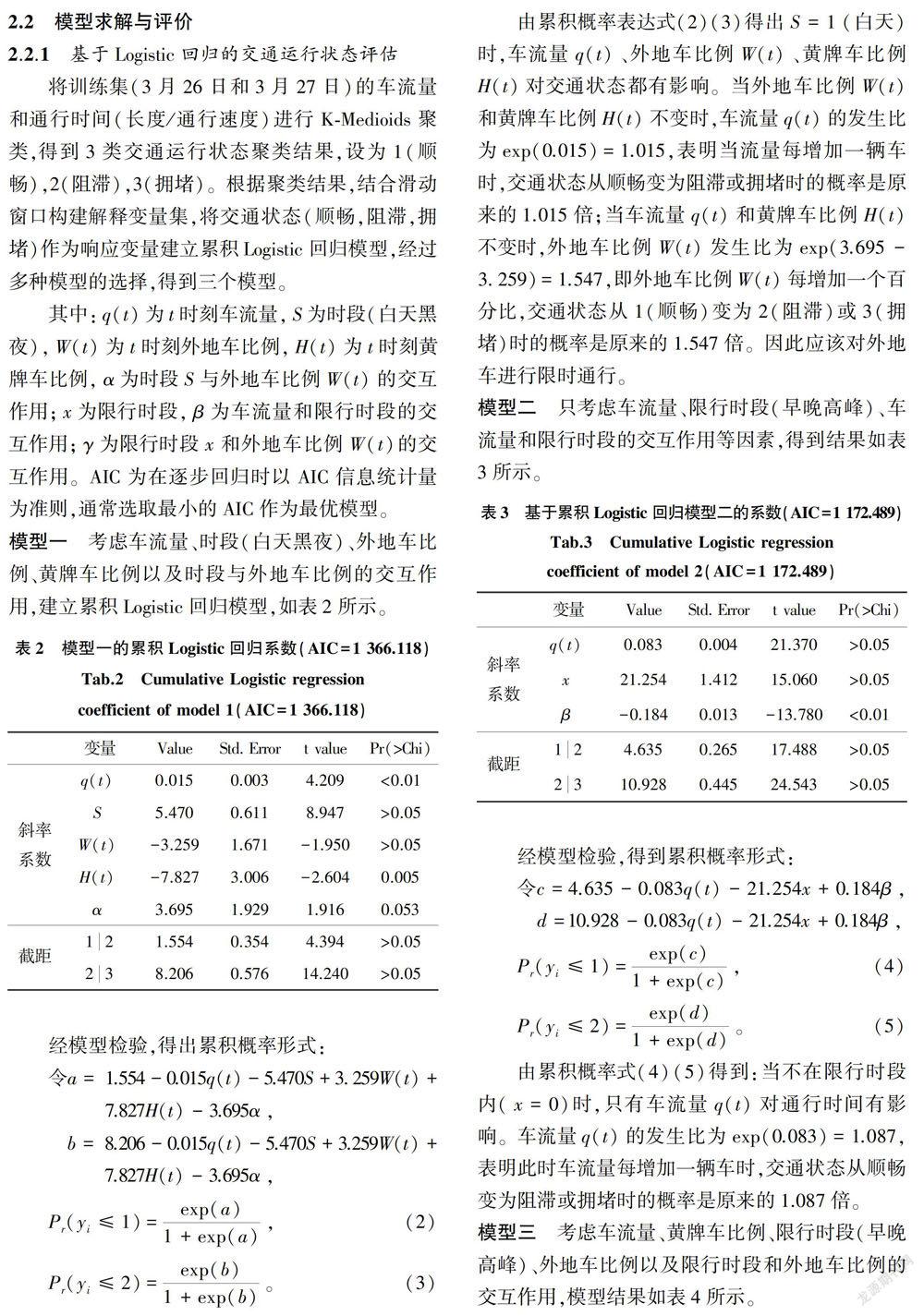
其中：q（t）为t时刻车流量，S为时段（白天黑夜），W（t）为t时刻外地车比例，日（t）为t时刻黄牌车比例，α为时段S与外地车比例W（t）的交互作用;x为限行时段，β为车流量和限行时段的交互作用;γ为限行时段x和外地车比例W（t）的交互作用。AIC为在逐步回归时以AIC信息统计量为准则，通常选取最小的AIC作为最优模型。模型一考虑车流量、时段（白天黑夜）、外地车比例、黄牌车比例以及时段与外地车比例的交互作用，建立累积Logistic回归模型，如表2所示。

由累积概率表达式（2）（3）得出S=1（白天）时，车流量q（t）、外地车比例W（t）、黄牌车比例H（t）对交通状态都有影响。当外地车比例W（t）和黄牌车比例H（t）不变时，车流量q（t）的发生比为exp（0.015）=1.015.表明当流量每增加一辆车时，交通状态从顺畅变为阻滞或拥堵时的概率是原来的1.015倍;当车流量q（t）和黄牌车比例H（t）不变时，外地车比例W（t）发生比为exp（3.695-3.259）=1.547.即外地车比例W（t）每增加一个百分比，交通状态从1（顺畅）变为2（阻滞）或3（拥堵）时的概率是原来的1.547倍。因此应该对外地车进行限时通行。

模型二只考虑车流量、限行时段（早晚高峰）、车流量和限行时段的交互作用等因素，得到结果如表3所示。

由累积概率式（4）（5）得到：当不在限行时段内（x=0）时，只有车流量q（t）对通行时间有影响。车流量q（t）的发生比为exp（0.083）=1.087.表明此时车流量每增加一辆车时，交通状态从顺畅变为阻滞或拥堵时的概率是原来的1.087倍。模型三考虑車流量、黄牌车比例、限行时段（早晚高峰）、外地车比例以及限行时段和外地车比例的交互作用，模型结果如表4所示。

由式（6）、（7）可得：当在限行时段内（x=1）时，x和外地车比例W（t）有交互作用。有车流量q（t），黄牌车比例H（t）和外地车比例W（t）对通行时间有影响。外地车比例W（t）和黄牌车比例H（t）不变，车流量q（t）发生比为exp（0.063）=1.065.车流量每增加一辆车时，交通状态从1（顺畅）变为2（阻滞）或3（拥堵）时的概率为原来的1.065倍，这意味着γ=2（阻滞）和γ=3（拥堵）的概率会增加。

为评估各模型的预测效果，将该路段3月26日和3月27日作为训练数据预测3月28日（一天共720个数据）的交通状态，并将预测状态与真实状态作对比（当预测状态和真实状态一致表示预测正确，不一致则表示预测错误），分别计算三个模型预测的正确率。其中3月28日真实状态为距三种状态的聚类中心最短距离时所对应的交通状态。设T、T、T分别表示真实状态为顺畅、阻滞、拥堵状态，P、P、P分别表示预测状态为顺畅、阻滞、拥堵状态。表5描述三个模型在各情形下的数据个数，其中每个模型下的9个数加起來为3月28日数据的总数量即720。

从表5计算正确率可得，模型一为59.58%，模型二为82.36%，模型三为80.280A，，比较各模型AIC信息统计量，模型二最小，因此在三个模型中，模型二能较好地测算出车辆增加时路段交通状态的变化。

2.2.2基于支持向量回归机的通行时间预测

上一节通过累积Logistic回归模型得出新增车辆对路段交通状态的影响，本节对新增车辆的通行时间进行预测。将累积Logistic回归的三个模型代人支持向量回归机中，运用滑动窗口法对窗口数^进行选择，如图2所示（图中用“o”表示：MSE达到最小的滑动窗口数）。

表6列出三个支持向量回归机（SVR-1.SVR-2.SVR-3）对通行时间的预测结果，可以看出：对于滑动窗口数，三个模型相差不大：但对比MSE，模型三的训练MSE和预测：MSE在这三个模型中最小。因此针对新增车辆的通行时间预测，模型三在这三个模型中是最好的。

图3更加直观的展现了SVR三个模型的通行时间真实值和预测值的对比，可以看出模型三比其他两个模型拟合效果稍好，但三个模型在下午4点至6点拟合效果不好，这可能是由于图1中3月28日的车流量数据（过车数）与实际不符造成的。整体来说，三个模型能够较好的预测出通过该路段的通行时间，可为市民提供参考建议。

3结论

通过对深圳市交通数据建立累积Logistic回归模型，研究结果表明：当只考虑车流量、限行时段和二者之间的交互作用时，模型正确率达到最高为82.36%，此时车流量在非限行时段每增加一辆车，发生比从顺畅状态转为非顺畅状态的概率是原来的1.087倍：结合支持向量回归机较好地预测出新增车辆的通行时间，其中考虑车流量、黄牌车比例、限行时段、外地车比例及限行时段和外地车比例的交互作用时，模型MSE最小，效果最优。此外基于Logistic回归的模型还说明，当外地车比例增加时，拥堵的概率会增大，因此应该对外地车进行限时通行来缓解高峰期时的交通拥堵状态。本文研究结果可为交通相关部门提供参考。