化归和转化思想在高中数学高考复习中的实施策略
2019-09-10揭用权
揭用权
【摘要】 化归和转化是高中数学中十分重要的一种思想方法,主要使复杂问题变得简单化,从而更轻松、高效的解题,在高考数学复习阶段,教师将化归和转化这种数学思想方法传授给学生,对于学生应战高考是十分有利的,本文之中笔者将从自身的实践教学经验出发,对化归和转化思想在高中数学高考复习中的应用实施提出相关建议。
【关键词】 化归和转化思想 高中数学 高考复习 实施策略
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2019)06-013-01
前言
高中數学知识体系复杂,在高中数学复习课中如何能够让学生感到简单易学,是困扰教师的问题,而对此笔者认为关键是让学生理解复习知识内容的本质,因此教师将数学思想方法传授给学生是十分重要的。其中化归和转化思想无论是在几何,还是在代数问题之中都非常适用,为此教师有必要强化化归和转化思想在高中数学高考复习中的实施。
1.化归和转化思想的解读
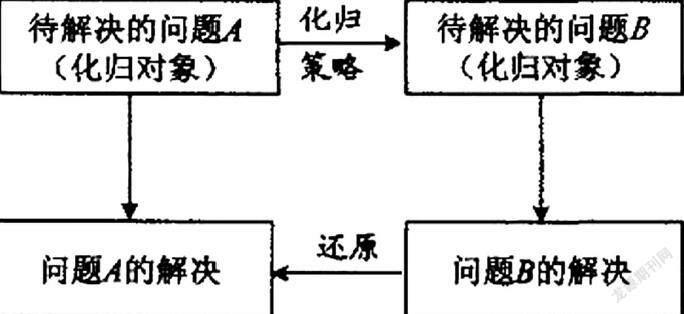
化归和转化是学生学习基础知识之后,解决综合问题的重要途径,因此在高中数学高考复习中化归和转化思想是十分适用的,可更好的帮助学生处理复杂问题,并建立知识与能力的桥梁。所谓化归和转化,即把数学问题视作研究对象,通过观察、分析、类比、联想等思维方法,从而将原有的复杂问题进行转化,变换为一个或几个相对容易解决的问题,从而实现数学问题的熟悉化、直观化、简单化、特殊化,这样学生就可以应用自身已知的方法和知识,去有效的化解数学解题困难,化归和转化思想的一般思路如下图示:
在整个高中阶段体现化归和转化思想的知识问题有很多,在运用化归和转化思想的过程中,可以尝试一般与特殊的转化、变量与常量的转化,还可以从数与形、函数与方程中去探索有利于解题的途径和方法,下面将结合自身的实践教学经验,对此作出详细的说明。
2.化归和转化思想在高中数学高考复习中的实施策略
2.1一般与特殊转化
在高中数学高考复习实施化归和转化思想的过程中,“一般与特殊转化”是最常见的一种方法,并且在高考选择题和填空题中经常应用,在解题的过程中,可以从特殊情况入手,从而去寻找解决问题的一般方法,同时也可以从一般情况出发,去解决特殊问题。如运用赋值法解客观题,就是利用了“当字母在规定范围内取任意值时命题成立,则此范围内的特殊值也成立”这一原理,从特殊情况入手,将一些字母一般取值下命题真假判断问题,转化为字母取特殊值时的命题真假判断问题,得出解题的一般方法,为学生的解题创造便利。而像这样的例子还有很多,在高中数学高考复习中,教师要引导学生善于运用“一般与特殊转化”的化归和转化思想,从而高效解题。
2.2变量与常量转化
“变量与常量转化”也是一种重要的化归和转化思想形式,也是需要教师在高中数学高考复习中需要教会传授给学生的。以这样的问题为例“不等式a|x|≥x恒成立,其中x∈R,求实数a的取值范围?”,在面对这一数学问题时,就可以运用到“变量与常量转化”的化归和转化思想,运用分离变量的方法,从x=0和x≠0两个方面出发,将不等式问题转化为函数最值问题,使一个复杂的变量问题,最终被转换为一个相对简单的常量问题,从而得出最终的答案。在高中数学高考复习中,运用“变量与常量转化”的化归和转化思想进行解题,教师要引导学生具备举一反三的能力,通过一个数学例题,学会对同类问题,类似求解。
2.3数与形的转化
在整个高中数学学习阶段,涉及“数与形转化”的化归和转化思想问题有很多,并体现在从“数→形”和从“形→数”两个方面,教师能够将这种化归和转化思想传授给学生,对学生解题能力的提升是很有帮助的,有助于学生取得更好的成绩。举这样的一个例子,如“已知△ABC顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0)”,若是C=5,求sinA的值”,在面对这一数学问题时,就可以通过“数与形转化”的方式进行解题,从而将几何问题转化为向量问题。从近几年的高考命题趋势可以发现,关于“数与形转化”的问题基本是在解析法上考察,在复习的过程中,教师应该注重从学生的数形转化意识训练入手,而在具体的技巧方面教师不必太过着力。
2.4函数与方程转化
在高中数学学习过程中,函数和方程是两个十分重要的知识点,但两者之间又存在相互转化的关系,其中函数是方程的中介,而方程是函数的基础,两者之间就像是“异卵兄弟”,因此在化归和转化思想在高中数学高考复习实施中,教师能够将“函数与方程转化”思想传授给学生,也是有助于学生高效解题的。举这样的一个例子,如“x的方程sin2x+acosx-2a=0有实数根,求实数a取值范围”,教师就可以引导学生通过方程与函数之间的转换,从而更加快速高效的进行解题。
总结
化归和转化作为一种重要的数学思想方法,在高中数学高考复习中是非常适用的,可以帮助学生加深对知识的本质认识理解,降低数学问题学习理解难度,但需要注意的是,化归和转化思想的成功应用是以“数学发现”为基础的,因此在数学高考复习阶段,化归和转化不能只停留在分析上,还应带领学生在各种题型中尝试练习应用,这样才能更好的为学生赢在高考做出保障。
[ 参 考 文 献 ]
[1]董诗林.化归转化思想方法在高中数学中的应用实践[J].上海中学数学,2016(04):40-42.
[2]李红金.高中数学课本中蕴含的化归转化思想方法[J].数学教学研究,2016,34(06):14-16+21.
[3]安宝琴.浅谈“化归与转化思想”在高中数学解题中的应用[J].数学学习与研究,2016(03):93.
[4]何玉春.化归和转化思想在高中数学教学中的体现和应用[J].中小学教学研究,2017(03):40-41.
