基于多维博弈的多产品定价策略分析

谢会芹 景勤娟 李凡 李昌明

摘 要：根据多维博弈理论，探讨具有需求替代性的多种产品定价策略静态和动态多维博弈模型，然后求解其Nash多维均衡，最后比较多维博弈与单独博弈均衡结果。并以河北省战略性新兴产业为例，具体研究该产业发展中的博弈与定价问题。

关键词：多维博弈;定价策略;河北;战略性新兴产业

1.引言

在现实市场中，为了满足消费者差异化需求，企业通常会提供多种相关产品，它们在功能定位、定价以及营销策略上都存在着一定的差异性，许多学者对多产品定价问题围绕着垄断厂商进行了大量研究。但现实经济活动中，企业的生产和销售大多数是在竞争环境下进行的。此时，由于多产品之间可能存在着一定程度的需求替代性，为了获得最大利润，每个企业在选择自己产品的定价策略时不仅要考虑竞争对手在该产品上的定价策略，还要同时考虑自己和对手在其它相关产品上的定价策略，这是一种多维博弈问题。

2.静态博弈与动态博弈比较

假设某地区有两个企业同时向当地市场提供种具有需求替代性的产品，并且垄断了该地区这种产品的市场，企业的利润函数为（其中：表示企业的第种产品的边际生产成本）：

（1）

在靜态多维博弈中，两个企业同时选择定价策略向量，此多维博弈问题存在一个纯策略Nash均衡[1]。企业的定价策略向量反应函数为

（2）

由式（2）可得维Nash均衡解为

（3）

其中：是阶单位矩阵，A、B、D均可推算，推算过程略。

在动态多维博弈中，不失一般性，假设企业1（领头企业）先行动，企业2（尾随企业）再行动。通过最优一阶条件，可得两个企业关于种需求相关产品定价策略动态多维博弈的子博弈精炼维Nash均衡解。

3.多维博弈与单独博弈均衡比较

在静态博弈条件下，当只对第种产品进行定价策略静态单独博弈时，企业的利润函数为

（4）

通过求解均衡发现，多维博弈下的维Nash均衡解分量与单独博弈下的Nash均衡解完全一样。因此，需求无关的种产品定价策略静态多维博弈模型下的维Nash均衡解是个分别关于每一产品的定价策略静态单独博弈模型的Nash均衡解的简单组合。

在动态博弈条件下，当只对第种产品进行定价策略单独博弈时，利用逆序法[2]，可得到需求无关的种产品定价策略多维博弈的子博弈精炼多维Nash均衡解为，发现多维博弈下的子博弈精炼多维Nash均衡解式分量与单独博弈下的子博弈精炼Nash均衡解和完全一样。因此，基于种需求无关产品定价策略多维博弈模型的子博弈精炼多维Nash均衡解是个分别关于每一产品定价策略单独博弈模型的子博弈精炼Nash均衡结果的简单组合。

4.以河北省战略性新兴产业为例分析

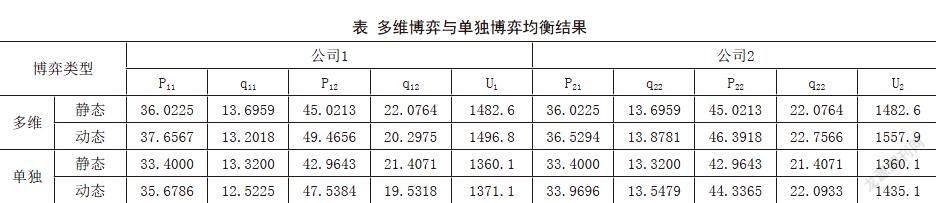
河北省两家半导体照明材料公司分别向石家庄市场提供两款照明材料，参数如下：，，，，，，，，，。由前面的分析可得多维博弈与单独博弈均衡结果（如下表）。

通过分析可知，需求无关多产品定价策略静态和动态单独博弈是特殊情况;在动态多维博弈中，两个公司的产品定价和利润高于静态多维博弈，其中，后动公司选择低价策略并获得更多市场份额和利润，即后动公司具有后动优势;多维博弈Nash多维均衡策略优于单独博弈Nash均衡策略。

参考文献

[1]Spence A M.Multi-product quantity-dependent prices and profitability constraints[J].Review of Economic Studies，47（150）：821-841.

[2]Maglaras C，Meissner J.Dynamic Pricing strategies for multiproduct revenue management problems[J].Manufacturing & Service Operations Management，2006，8（2）：136–148.

课题：2016年河北省社会科学基金项目（编号：HB16YJ052），2018年度河北省人力资源和社会保障课题（编号：JRS-2018-3036）