顺学而教：数学教学的应然追求

张卫星

现代教学理论认为：学生不应是被动接受知识的容器，而应是主动参与学习的主体。美国教育家拉夫尔·泰勒说过：“学生的学习取决于他自己想学什么，而不是教师要教什么。”由此可见，数学教学要尊重学生的意愿，做到顺学而教。所谓顺学而教，即扣准学生学习的脉络，从学生的实际出发，顺着学生的思路展开教学，努力让教学呈现出真、实、透的理想状态。只有顺学而教，才能让数学教学多向互动、动态生成，从而让数学课堂充满活力，轻负高效。那么，如何做到顺学而教呢？下面，笔者以“用数对确定位置”一课的教学为例，阐述自己对这一观点的理解。

数学是思维的科学，数学教学必须要关注学生的思维发展。小学生思维发展的基本特点是以具体形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式，但是这种抽象逻辑思维在很大的程度上仍然是直接与感性经验相联系的，仍然具有很大成分的具体形象性。如果教师能厘清每一堂课中学生应达到的思维水准，就可以让教学更加贴近学生的实际，更有针对性，从而让顺学而教成为现实。那么，如何厘清学生的思维水准呢？关键是要用心研读教材。数学教材是众多教育专家、教学专家、心理专家、优秀教师的思维结晶，其在编排时就蕴含了学生应该达到的思维水准。如果我们能够理解这些“蕴含”，就能较好地厘清学生的思维水准。

例如，人教版《义务教育教科书·数学》五年级上册第19页“用数对确定位置”中的例1，从现实的座位图演变到规则的几何图，其实蕴含了半抽象的数学思想，表明学生要经历半抽象的思维历程。教材以规则的几何图为载体，让学生理解行与列的概念，并且明确行——从前往后，列——从左到右，然后提出确定位置的规则——先列后行，在此基础上提出数对这一概念并让学生经历数对的再创造过程。其中，实现半抽象的关键是学生视角向教师视角的转化。

又如，人教版《义务教育教科书·数学》五年级上册第20页中的例2，从规则的几何图演变成标准的坐标图，表明要让学生经历全抽象的思维过程。只有经历了全抽象，学生才能真正理解“数对”的内涵。教材以座标图为载体，让学生体验数对的确定性和唯一性。所谓确定性，即座标图中的每一个点都能用数对表示;所谓唯一性，即座标图中的每一个点的数对都是不同的。

可见，厘清学生思维水准的依据是教材。因此，教师要静下心来解读教材，力求让教材发挥最大的作用，力求让顺学而教的前提更接地气。

学生的阅历相对浅显，他们对这个变幻的数学大世界充满了好奇的心理，于是产生了强烈的探索未知的欲望和需求。他们常常因为探知到某些问题的答案而激动，为达到“知道”的目的而执着。探知的需求与教师施加的教育影响相碰撞时，就能形成良好的教育效果，它能驱使学生去积极获取知识，参加实践，改变自己的不良习惯。因此，我们在数学教学中要为学生创设探知的情境，让学生产生探知的需求，并顺势为他们的探知提供时间和空间。唯有如此，顺学而教才更具含金量。

例如，在教学“用数对确定位置”时，笔者经历了如下教学片断。

师：这是张亮班的座位表，谁知道张亮的位置在哪里？

生：没信息，不能判断。

师：哦，没信息，不能判断对吗？

师（出示“他在第2列”）：现在能确定了吗？

生：一条信息不够，还是不能确定。

师（又出示“他在第2列、第3行”）：现在能确定了吗？

生：现在可以确定了。

师：看来，要确定张亮的位置至少需要几条信息？

生：两条。

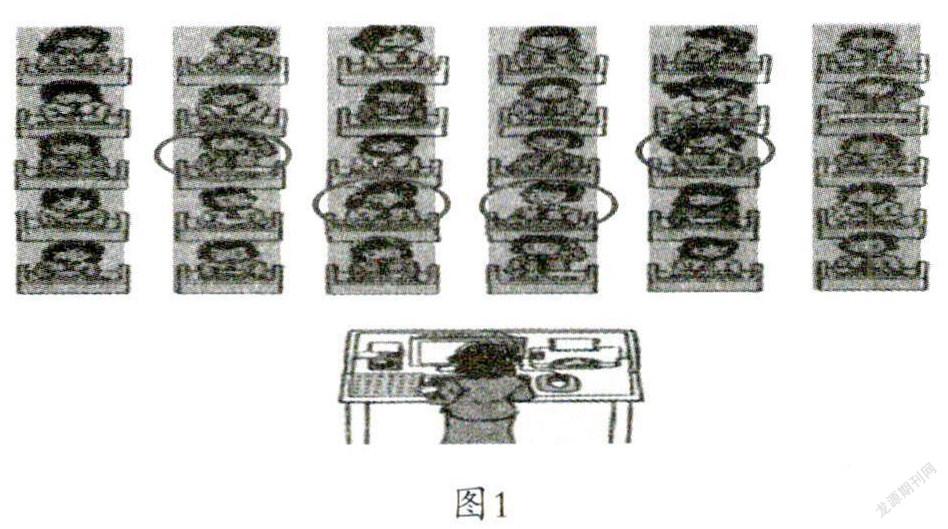
師：大家都知道张亮的位置在哪里，谁能用自己的语言汇报一下？（结果，四个学生汇报的位置都不同，如图1中的画圈处。）

师：为什么会出现四个位置？

生：因为有的人是按从左到右的顺序来确定的，有的人是按从右到左的顺序来确定的，有的人把横着的排当成列，有的人把竖着的排当成列。

师：原来是大家观察的顺序和方向不一样。看来，位置的确定还需要一个共同的……

生（异口同声）：规定。

师：对，位置的确定真的需要一个共同的规则。

上述教学中，教师先通过“没信息—一条信息—两条信息”的演变，让学生深刻感受到了确定班级中的位置至少需要两条信息。接着，又通过对两条信息确定四个位置这一现象的剖析，使得学生内心自发产生一种需要：确定位置除了两条信息还不够，还需要一个共同的规则。可见，满足学生的探知需求是实践顺学而教的关键。

创造欲望是人类与生俱来的一种本能。苏霍姆林斯基说：“人的心灵深处都有一种根深蒂固的需要，那就是希望自己是一个发现者、研究者、探索者。”小学生的数学创造欲望是一种朦胧的、潜藏的、无意识的本能，它没有明确的、稳定的指向，它需要教师在教学中来激活。可以说，学生的数学创造欲望在很大程度上是数学教育的产物，它的强弱完全取决于课堂上所受的教育和熏陶。通过教师的正确引导和有效诱发，学生的创造欲望会得到强化，创造本能会逐渐被激活，数学创造的行为指向也会更为鲜明、稳定。因此，我们在数学教学中要满足学生的创造欲望。唯有如此，学生的创造性思维才能萌发，他们才会有坚定的信心去进行创造性实践，从而让数学学习真正成为一种再发现、再创造的过程。

例如，在教学“用数对确定位置”时，笔者经历了如下的教学片断。

师：刚才我们都是用列和行来描述这些不同的位置，你们能用更简洁的方法表示张亮的位置吗？请将表示方法写在作业纸的反面。（学生开始思考并书写）

师：谁来展示一下？

生：2列3行。

师：把两个“第”字省略了，的确简洁了。还有不同的吗？

生：（2L，3H）。

师：2L与3H表示什么意思？

生：2L表示2列，3H表示3行。

师：为什么中间写了个逗号？为什么加了个小括号？

生：逗号可以把列与行隔开，看起来更清楚，加小括号表示它们是一个整体。

师：你的想法与众不同，谢谢你的回答。还有不同的吗？

生：（2，3）。其中2表示第2列，3表示第3行。

师：你就用两个数字来表示，真的是很简洁的一种方式。

师：请看刚才的三种表示方法，它们有什么共同的特征吗？

生：它们都包含两条信息。

生：它们都是先列后行。

生：它们都有2和3两个数字。

师：（2，3）是一种最简洁的表述方式，我们一般就把这种表示方法叫做数对，读作数对（2，3）。

上述教学中，教师先让学生用简洁的方式表示张亮的位置，然后根据学生的创造性回答进行分析与提炼，让学生真正感受到（2，3）是最简洁的表示方式，在此基础上揭示数对的含义，学生对数对内涵的理解也就水到渠成。可见，激发并满足学生的创造欲望是顺学而教的核心所在。

思维的拓展应在学生现有水平和潜在经验的基础上进行，是学生不断试误、纠误的过程，也是学生对已有经验的丰富、扩充、修正、改造，是不断完善认知的过程。因此，教师要借助多样化的教学活动来培养和拓展学生的数学思维，顺应学生思维能力发展的需要，让学生既“知其然”又“知其所以然”，进而在提高学习能力的同时，也为其良好的思维发展奠定坚实的基础。

例如，在教学“用数对确定位置”时，笔者经历了如下的教学片断。

师：下面我们来做一个游戏，请大家听清要求。请数对是（1，1）的同学站起来;请数对是（1，2）的同学站起来;请数对是（1，3）（1，4）（1，5）（1，6）的同学站起来。

师：你们发现这6位同学的数对有什么特征吗？

生：第一个数都是1。

生：他们都在第一列，所以第1个数都一样。

生：第1个数是1，表示他们都是第1列的。

师：看来同一列的同学，数对中的第1个数都相同。这6位同学有6个数对，能不能用一個数对同时表示这6位同学？

生：用数对（1，X）表示。

师：X表示什么？

生：X表示所有的行。

师：大家同意他的说法吗？（学生纷纷表示同意）

师：不过，数学上一般用（1，Y）表示所有第1列的同学。

师：继续游戏，请数对是（1，3）（2，3）（3，3）（4，3）（5，3）（6，3）的同学站起来。

师：他们的数对又有什么特征？

生：他们的数对第二个数都是3，表示他们都在第三行上。

生：他们都在第三行，所以第二个数字都是3。

师：能用一个数对表示第三行的所有同学吗？

生：（Y，3）。（学生纷纷同意）

师：数学上一般用（X，3）表示所有第三行的同学。

师：大家发现数对上的字母有什么特点？

生：列用X表示，行用Y表示。

师：对，数学上就是这么规定的。请你们再思考一下，如果要用一个数对表示全班的同学，这个数对又是什么呢？

生（异口同声）：数对（X，Y）。

上述教学中，教师通过游戏让学生明白了同一列的数对，第1个数相同;同一行的数，第2个数相同。同时通过拓展，让学生明白了数对中有未知数，表示的是很多位置，而不是一个位置。这样，就自然而然地让学生认识到数对的丰富内涵。数对（X，Y）的得出表示学生已深刻理解了数对的内涵。可见，促进学生的思维拓展是顺学而教的重心所在。

解决问题是指在某种情境的初始状态和渴望达到的目标状态之间存在障碍的前提下，运用一系列认知操作，扫除障碍，将问题的初始状态转化为目标状态的思维过程。解决数学问题的能力是学生内在素质的反映，是数学综合能力的体现。因此，数学教学要着力于提高学生解决问题的能力，要有目的、有计划地安排教学环节，促使学生解决问题能力的提高。唯有如此，学生学习数学的兴趣才会越来越浓，顺学而教才能走进良性循环的轨道。

例如，在教学“用数对确定位置”时，笔者设计了如下几个问题。

（一）找一找

请快速确定图2中七种中药的位置。

（二）认一认

（三）标一标

1.图5中是怎样确定棋子位置的？说一说黑方王与白方后的位置。

2.白方（g，3）处的马进到（f，5）处，黑方（d，6）处的兵进到（d，5）处。你能分别标出它们移动后的位置吗？

（四）想一想

图2重在让学生理解数对在中医药橱中的应用;图3、图4重在拓展数对的应用范围;图5重在让学生理解数对在国际象棋中的应用;图6重在训练学生的综合思维能力。可见，提升学生的解决能力是顺学而教的目的所在。

（责任编辑：杨强）