数学深度学习的内涵及基本实践问题
2019-09-10孙学东



摘要:数学深度学习有高投入、高认知、基于任务情境、指向数学核心素养等内涵。数学深度学习实践中有一些经常出现的问题需要辨析:深度学习不等于简单地增加学习难度,而是要增强处理问题过程的思维复杂性,从而探寻数学内容的核心与本质;深度学习不等于不需要内容的广度,而是要“以深度带广度”,从而“为迁移而教”;数学基础知识也需要深度学习,要以“不简单”的任务反衬“基础”的重要性;学业水平落后的学生也需要深度学习,要为他们循序渐进地设置思维进阶的问题。
关键词:数学深度学习难度广度基础知识落后学生
近年来,数学课堂中的“深度学习”研究与实践渐成趋势,其中也出现了一些认识误区。如不及时厘清数学深度学习的内涵及认识误区,将使数学深度学习的实践僵化、泛化甚至异化。本文试对数学深度学习的内涵及教学实践中经常出现的问题做一些解读和辨析。
一、数学深度学习的内涵解读
德国教育家赫尔巴特认为:真正的学习与课程,意味着登山式的挑战与冲刺。同样地,数学教学不能总是让学生在舒适的山谷中游荡,而要让学生练习攀登山峰、掠过草地与沼泽,获得广阔的视野。任何没有深度、没有思维含量的学习内容都不能引发学生的学习兴趣,提升学生的学习品质。
实践探索中,我们这样理解数学深度学习:在教师创设的具有挑战性的问题情境中,学生全身心地投入、高阶认知参与的有意义的学习过程。具有挑战性的问题情境意味着经过加工整合后的素材复杂性的增强;学生学习不能仅仅记知识、仿技巧、套题型,而需要具身参与、运用高阶思维,在此过程中理解数学核心知识,掌握数学本质和方法,把握数学思维方式,并形成积极的内在动机和正确的价值观念,从而获得自身素养的全面发展。
数学深度学习有这样的内涵:一是高投入,即全身心地投入。情绪和认知是相互关联的,数学深度学习的表现是好奇、期许、兴奋、少许的迷惑、些许的遗憾、会心的欢笑等等。二是高认知,即以理解为起点。数学深度学习是触及知识核心和本质,探查知识之间的相互联系,基于理解,更多地关照分析、评价与创造层面的高阶思维的学习。三是基于任务情境,即通过真实情境的任务驱动,在数学活动中解决问题。数学深度学习需要教师在单元整体设计的基础上,将教学内容任务化,任务问题化,问题情境化。四是指向数学核心素养,或者说指向数学的本质联系及思想方法。数学核心素养的属性决定了其習得必然依赖于深度学习;而数学核心素养一旦形成,又会有力地支撑深度学习——两者是相互加强的互动循环关系。指向数学核心素养,使深度学习有了超越解题的目标旨归,让数学学习真实发生。
二、数学深度学习教学实践中经常出现的问题辨析
(一)数学深度学习就是增加学习难度吗?
深度与难度是两个不同的概念:深度是触及知识核心与本质的程度,而难度则是完成学习内容的困难程度。有深度的课堂不一定难度大;相反地,难度大的课堂不一定有深度。数学深度学习不是加大学习内容的难度,让学生感到沮丧进而失去学习的主动性;相反地,正是通过提升问题的复杂性,让学生增进学习的兴趣并且理解相关内容的本质。如果认为数学深度学习就是加大学习难度,就有可能出现这样的现象:教师为了在有限的时间内完成教学,尽快地将自己对知识和方法的理解,以自认为结构化的方式传输给学生,使学生的学习从以往的“课上记笔记,课下练笔记,考试套笔记,考后全忘记”变成“课上记模型,课下练模型,考试套模型,考后全无形”。
当然,数学深度学习是在经过精心加工的、具有挑战性的问题情境中发生的,旨在激发学生的学习意向,让学生触摸数学知识的核心与本质。指向深度学习的数学问题难度会适当增大,它往往表现为处理问题过程中思维复杂性的增强,这是探寻数学内容核心与本质的必需。
比如,在“一次函数、一元一次方程和一元一次不等式”的教学中,有这样的情境:“甲、乙两商场的某款西装和领带定价都是800元/套和100元/条。促销活动期间,甲商场的优惠方案是:买一套西装送一条领带;乙商场的优惠方案是:西装和领带均打9折。某公司欲购买20套西装和多于20条领带。”
对此,如果转化为这样的问题:(1)设购买x条领带,在A商场购买一共需付y1元,在B商场购买一共需付y2元,请分别写出y1、y2与x的函数关系式;(2)你能借助函数图像,说明选择哪家商场更合适吗?这两个问题就是常规、封闭、操作性的浅层次学习问题。
而如果分解成这样的问题:(1)购买30条领带,选择哪家商场更合适?45条呢?(2)该公司到底选择哪家商场更合适?请给出方案。(3)丙商场同款西装、领带定价和甲、乙商场都相同,它的优惠方案是:送10条领带,其余领带打8折。此时选择哪家商场更省钱?这个问题串就具有非常规、开放性和思辨性的特征:问题的复杂性增加,使得没有现成的解决方法可供借鉴,并且解决的方式不唯一。
在方法的比较和评价过程中,学生能够体会到“抽象数学问题,建立函数模型”可以更直观地解决问题,从而实现由常量数学向变量数学的飞跃。
(二)数学深度学习就不需要内容广度吗?
相比于接受式的浅层学习,发现式的深度学习需要花费更多的时间,因此,常会出现“课堂容量不足”的现象。但是,这并不意味着数学深度学习就不需要内容广度。《老子》有云:“为学日益,为道日损;损之又损,以至于无为,无为而无不为。”对于数学学习而言,不能仅仅满足于具体知识的学习和“一题一法”小技巧的获得,更要追求蕴藏在知识与技能中数学思想的提炼和数学思维的锤炼,最终升华为通彻。华罗庚先生在指导青少年儿童时说:“‘化’了以后能够用,能够活用,能够适应各种各样具体情况来活用。”这里,“化”的标志就是知识和方法的迁移。
少即是多,慢即是快,通彻的东西是具有迁移能力的。数学深度学习正是在“以深度带广度”的过程中获得迁移能力,不断体现和发展数学的基本素养。
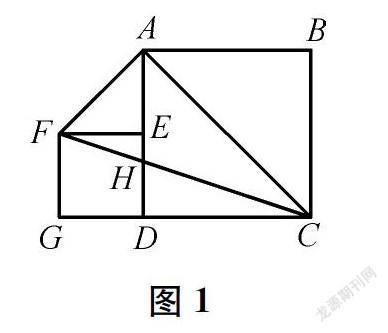
比如,有这样一道题:如图1所示,正方形ABCD的面积为25,正方形EFGD在它旁边,且A、E、D和C、D、G分别共线,连接AF、CF、AC,求△ACF的面积。初中生解决这个问题常用的方法是:设正方形EFGD边长为a,则S△ACF=5×(5+a)-12×25-12a(5-a)-12a(5+a)=12.5。教学若到此为止,则着实可惜。
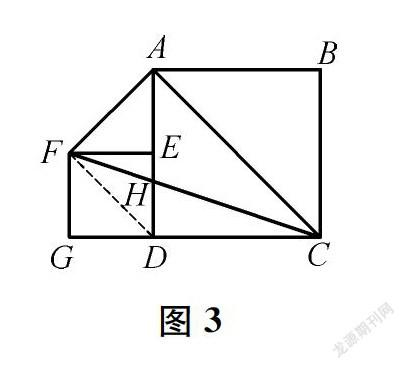
教师应该引导学生多角度思考:△ACF的面积是正方形ABCD的一半,是偶然还是必然?从而得到这样几种方法:(1)设正方形ABCD的边长为b,列式后得到S△ACF=12b2=12S正方形ABCD;(2)如图2,延长FE,分别交AC、BC于点I、J,S△ACF=12FI·AE+12FI·CJ=12FI(AE+DE)=12FI·AD,因为FI=CD,所以S△ACF=12CD·AD=12S正方形ABCD;(3)如图3,连接FD,FD∥AC,所以S△ACF=S△ACD=12S正方形ABCD。
上述学习过程花费时间较多,但是学生经历了“发现问题—猜想结论—多角度论证”的过程,发现问题的眼光得到锻炼,从复杂到简单(从抽象到直观)理解结论的方法得到激活。以上三种方法是数学问题解决的基本方法。方法1显示了字母代替数的一般性价值;方法2不同于方法1的“补”,而是“割”,它们都是求解图形面积的基本方法;方法3能更直观地发现结论。一个问题“想”明白了才是真的“懂”了,深刻体验、深层理解这些方法才能产生迁移以解决更复杂问题的能力。
(三)数学基础知识不需要深度学习吗?
数学基础知识因为其综合性较弱,往往被等同于简单知识。事实上,“基础”不等于“简单”,不能肤浅理解和机械训练;它是一种必需和奠基:复杂的数学问题解决不了的原因很多时候是对基础知识的理解不够深刻、运用不够灵活。从这个意义上来说,基础知识更需要经过深度学习的过程,以此深刻理解其从何而来、去往何方以及在问题解决过程中的价值。
数学深度学习之于基础知识,需要从单元整体的角度加以整合,以“不简单”的问题反衬“基础”的重要性。
比如,苏科版初中数学七年级上册《代数式》一章最后一节《整式的加减》中,有整式加减法则“有括号先去括号,再合并同类项”这一基础知识。因为此前学生已经用两个课时分别学习了“合并同类项”和“去括号”,有教师就上成了练习课。一节课练下来,50个学生的班级里有40多个学生能够准确地进行整式加减运算,但是一段时间后,可能只有30个左右的学生还能准确地进行整式加减运算,而基本上极少有学生能利用整式的加减解决问题。
因此,应该换一种教学方式。首先,提出问题:一个两位数,交换它的十位数字与个位数字,得到一个新的两位数。研究这两个两位数的和,你有什么发现?能解释一下你的发现吗?尝试几个数字后,有学生意识到和是11的整数倍。但是,怎么解释呢?有学生用生活语言进行了说明:“颠倒十位与个位再相加,和的个位与十位是一样的,所以是11的整数倍。”但是,39+93的个位与十位数字之和都大于10,好像解释不通了。有学生试图尽可能多地举例,发现和都是11的整数倍,但是难以穷尽……自然语言难明其理,小学算术难以穷尽,就得有新的方法出现。有学生设原来十位和个位分别是x和y,得到(10x+y)+(10y+x)=11x+11y,结论不言而喻。那这两个数的差呢?这次,学生迅速得到(10x+y)-(10y+x)=9x-9y,结论一目了然。然后,引导学生体会新方法的产生过程:用字母表示数,列代数式,将代数式化简。指出:“这里化简的实质就是整式加减。看来整式加减是问题解决过程中很重要的一步,有必要进行研究。”接着,让学生再举几个整式加减的例子,经历多个整式加减的运算过程,总结化简整式的方法:有括号先去括号,再合并同类项。最后,引导学生总结自己本节课的发现经过:假设—否定—再假设—再否定—再假设……
没有解题的套路,只有不断地分析、评估、理清自己看问题的一般思路;将自己学过的知识迁移来解决一个开放的问题,对于學生而言就是创造“新方法”的过程。因此,学生获得的不仅是知识,还有知识以外的深刻经历:感悟具体知识中蕴含的数学思想方法,探究问题解决的核心策略,体验数学的思维方式。
(四)学业水平落后的学生不需要深度学习吗?
数学学业水平落后的学生常被认为不需要数学深度学习,理由是他们掌握基本的数学知识、技能,并在数学解题的过程中加以回忆和使用,就已经很不错了。事实上,这样的学生更需要通过深度学习获得数学思想方法、思维方式和理性精神,以此适应未来的生活和工作。部分学生正是因为通过机械模仿式的“低投入”学习获得“高产出”的分数,导致学业水平落后:当学业难度较低时,通过简单记忆和操练就能获得分数,由此养成了不良的学习习惯;当学业难度加大时,就会产生畏难情绪,难以开启思维。部分学生只是数学基础相对欠缺,但是具有较好的开放性和发散性思维,在问题解决过程中表现出的分析、评价和创造层面的思维能力有时并不输于学业水平较高的学生。还有部分学生正是因为在低水平的学习任务上消耗了大量的时间和精力,同时也消耗了学习的兴趣,从而在数学学业水平上显得落后。
对于数学学业水平落后的学生,教师不能一味地设置浅层次的学习问题,以貌似迎合学情,而要从学生的已有知识储备和能力基础出发,循序渐进地设置思维进阶的问题。
比如,教学“探究y=6x的图像及性质”时,教师通常设计任务:请将表格补充完整,并在平面直角坐标系中描点、连线,画出反比例函数y=6x的图像。面对这样的任务,学生无须灵活、批判、创造性地思考,只需将以往现成的知识搬运填写。
其实,可以这样设计问题:(1)(由数猜形)你能由反比例函数y=6x的表达式,猜想这个函数的图像可能具有哪些特征吗?在平面直角坐标系中大致(无须精确)画出你认为的可能的“样子”。(2)(为数配形)类比一次函数图像的作法,通过列表、描点、连线的方式,在平面直角坐标系中画出反比例函数y=6x 的图像。(3)(数形结合)将问题(1)和问题(2)联系起来看,问题(1)中的一些结论还成立吗?反比例函数y=6x 的图像还有哪些特征?(4)(联想迁移)你能快速画出y=-6x的图像吗?在问题(2)的平面直角坐标系上画出。
上述问题设计有明显的不同层级思维的要求,使得不同层次的学生都有发挥自己思维特长,获得相应结果的机会。观察、联想、描述、验证、概括、推演、应用,这一系列的思维过程能很好地锻炼学生思维的灵活性、创造性和批判性。
当然,数学深度学习教学实践中需要厘清的问题还有很多。比如,数学深度学习不等于所有的教学及评价都要着眼于深入的理解;对于特定的课程内容和年龄阶段,需要选择合适的深入程度。这些还需要我们在实践中不断深入思考和辨析。
参考文献:
[1] 孙学东,周建勋.数学“深度学习”是什么?常态课堂如何可为?[J].中学数学教学参考(中旬),2017(5).
[2] 华罗庚.华罗庚科普著作选集[M].上海:上海教育出版社,1997.
