例谈初中生数学抽象能力的培养

姜鸿雁　赵维坤

摘要：基于2018年江苏省义务教育学生学业质量监测中主要考查数学抽象能力的8个小题及6个师生问卷题的监测结果，对初中生数学抽象能力的培养提出教学建议：创设氛围，引导学生体会“具体”与“抽象”的辩证关系;搭建平台，助力学生“理性抽象”能力的形成;放手阅读，让学生“穿行”于各种语言之间。

关键词：学业质量监测 数学抽象能力 感性具体 理性抽象 数学语言

数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的能力。主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征。数学抽象具体表现在四个方面：一是感悟现实生活中数的意义，估算运算结果;二是用符号表示数、数量关系和变化规律;三是从数量与数量关系、图形与图形关系中抽象出数学概念;四是借助符号进行运算和推理，抽象出一般规律和结构。数学抽象能力从高到低可以分为A、B、C、D四个水平。

数学抽象是数学关键能力的构成要素，是最基本的数学思想，是数学自身发展、应用的基础。它源于现实又高于现实，基于具体又高于具体，体现“九九归一”“和而不同”的哲学思想。培养学生的数学抽象能力，就是培养学生“用数学眼光观察世界”的能力和“透过现象看本质”的认识事物的本领，对学生的终身发展有着不可替代的作用。

2018年江苏省义务教育学生学业质量监测中，共设计了8个小题（下文提到的每一个试题都是其中之一，用字母与数字的组合进行编号）主要用以考查学生的数学抽象能力。本文根据全省46262名八年级学生的测试成绩、问卷调查以及4573名数学教师的问卷调查得到的数据分析，对初中生数学抽象能力的培养提出相应的教学建议。

一、创设氛围，引导学生体会“具体”与“抽象”的辩证关系

数学因为高度抽象，让不少学生望而却步，让不少人认为是“冰冷的美丽”。所以在教学过程中，面对一个个具体现象，要让学生充分经历“观察，思考它们背后的共性，并表达这一共性”的过程，体会到“抽象”是一个个“具体”现象共性的表达，产生“九九归一”之感;同时，面对“抽象”的结果，也要让学生赋予它一个个“具体”的背景，使它富有“活力”，感受到抽象背后的“和而不同”。

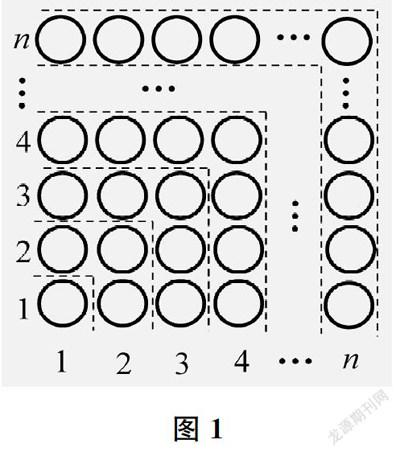
试题M8BS111根据图1计算：1+3+5+7+…+（2n-1）=。（结果用n表示，其中n是正整数）

本题主要用来测试学生“借助符号进行运算与推理，抽象出一般规律和结构”这一数学抽象具体表现的水平状况。本次测试中，本题的平均得分率只有45.6%，解答不正确的占43.4%，没有作答的占11.0%;数学总体能力处于A、B、C、D四个水平的学生在此题上的平均得分率分别为70.6%、25.0%、7.0%和2.8%。这与命题时预估的得分率62%有一定的差距。

由学生的错误解答可以看出，有超过一半的学生不能够自如地在符号语言、图表语言之间切换。他们面对图中的多个“┐”组成的图形，不能发现数字之和与小圆圈总数、小圆圈总数与小圆圈构成的“正方形的边长和面积”之间的关联。如果学生能在“抽象”与“具体”之间自如穿梭，面对这个问题，就能够自觉地转化到简单的具体的情形：当n=1时，图形是什么样的，结果是什么？当n=2时，图形变成什么样，对应结果是什么？n=3呢？n=4呢？……其中蕴藏的规律便会在这一个个“具体”中慢慢显露出来，解决本题就不困难了。这一思维过程体现了化抽象为具体、化一般为特殊、化难为易的思想方法。

“用字母表示数”是初中阶段正式跨入“数学抽象殿堂”的标志，对整个初中阶段各个数学领域的学习都会产生深远的影响。下面便是笔者设计的苏科版初中数学七年级上册第3章第1节“用字母表示数”教学中具有代表性的两个环节。

环节1

2+3=3+2;1/2+（-3）=（-3）+1/2;（-6）+（-3/5）=（-3/5）+（-6）。请同学们模仿以上例子，写几个类似的式子。

设计该环节时，预设学生在仿写的过程中，首先会慢慢在心理上感觉到“麻烦”，其次会发现仿写的式子之间的共性，第三会联系小学时学过的加法交换律，从而产生用字母表示数量关系的愿望与结果。事实上，在课堂上，仿写到第六位学生时，他直接说道：“像这样的式子写不完啊，直接a+b=b+a！”这句话道出了数学抽象的魅力。

笔者认为，“用字母表示”最好不是教师发出的“指令”，而是学生内心自发的需要。这是学生“认可”数学抽象的好机会。把握好这个机会，需要教师替学生创造“内需”的氛围。所以，笔者给足学生“仿写”的时間，“逼”学生感到这样写下去无穷无尽，“逼”学生思考并发现不同式子之间的“共性”（本质），并产生表达这一本质的愿望。

环节2结合生活实际，对于式子（1-10%）a，你希望字母“a”表示什么？

该环节旨在给学生开放的空间，创造由“抽象”回到“具体”的氛围。学生的回答让笔者欣慰，诸如：“我希望是我们国家沙漠的总面积，这样我们的环境会越来越好。”“我希望是病人的人数，这样健康的人越来越多。”……向善是人性之本，育人在潜移默化之中。

数学抽象对抽象思维能力要求高，数学抽象能力不可能经过一节课或几节课便形成。教师心中装载着“抽象”与“具体”的辩证关系，充分为学生提供体验的机会，让学生经历“火热的思考”，切实体会到“具体”的“形象性”、“抽象”的“必要性”，从而既喜欢“具体”，又亲近“抽象”，最终能够面对“具体”提炼“抽象”，面对“抽象”回归“具体”，并形成思维的习惯，数学抽象能力的培养便落地生根了。

二、搭建平台，助力学生理性抽象能力的形成

从现实到数学，是“感性具体”到“理性具体”的过程。随着研究的深入，学生还得经历“理性具体”到“理性抽象”的过程：在较为复杂的情境中识别数学概念，根据对象的意义、性质判断对象的属性以及其与相关对象之间的联系与区别;利用数学语言准确地描述数学对象的特征，并进行多方面的解释。在教学过程中，教师要对学生的学习起点作准确的预估，准确定位学生的“最近发展区”，在适当的时期给学生搭建适宜的“脚手架”（平台），助力学生逐步形成“理性抽象”的能力。

试题M8AS162如图2，分别以线段BD的端点B、D为圆心，相同的长度为半径画弧，两弧相交于A、C两点，连接AB、AD、CB、CD。若AB=2，BD=2√3，求四边形ABCD的面积。

本题主要用来测试学生“从图形与图形的关系中抽象出数学概念”这一数学抽象具体表现的水平状况。本次测试中，本题的平均得分率为69.1%，数学总体能力处于A、B、C、D四个水平的学生在此题上的平均得分率分别为93.4%、66.7%、9.2%和0.2%。

分析错误解答，可以得到如下几个主要原因：一是不能从作图过程中抽象出四条边都相等的信息，导致无法得到菱形的概念，自然无法解决问题;二是菱形的结论纯属“目测”，主观感觉得到，没有经过逻辑推理证明，所以不是运用对角线的性质解决问题，而是过顶点A作对角线BD的垂线，并“默认”垂足平分BD，“默认”△ABD与△CBD的面积相等;三是运用勾股定理时，只记“平方和”的形式，不识别斜边与直角边，得到错误答案221;还有二次根式运算不过关等。

抛开数学运算方面的错因，不难发现，无法从作图的情境中抽象出所画的图形是菱形，是最主要的错因。这给我们一个启示：学生在“理性抽象”的过程中，需要必要的“脚手架”（平台）助力。以本题为例，可能在不少教师眼里，由这个作图过程得到菱形的概念不难，但是对于八年级的学生来说，其实不然。虽然学生在小学里已经认识了圆，会用圆规画圆（此时画出的圆，笔者称为“理性具体”，因为毕竟不同于具体的圆形实物），但是对圆的本质——到定点的距离等于定长（笔者称为“理性抽象”）的学习在九年级。根据笔者多年的教学经验，在九年级学过圆的概念后，学生还需要一定时间的顺应与同化，更何况是八年级的学生？

教师面对教学内容要有“高观点”，面对学生还要“俯下身”。例如，从七年级到八年级，学生已经多次接触尺规作图，比如作一个角等于已知角、作已知角的角平分线、作已知线段的垂直平分线等。在必要时，教师要把所画的圆弧上的点与圆心连起来，让“心目中”的半径——那些相等的线段“可视化”，从“无形”到“有形”，便于学生抽象出图形与图形之间的关系;还要引导学生思考作图背后的数学原理，从而既有利于发展逻辑推理这一关键能力，又有利于从图形与图形的关系中抽象出数学概念。

三、放手阅读，让学生“穿行”于各种语言之间

解决一个数学问题的过程，常常是先阅读自然语言，从中提炼数学信息，再对信息进行加工，从而选择适当的数学模型解决问题。能够在自然语言、符号语言、图形语言、表格语言之间自如地切换，是数学抽象能力初步形成的标志。

试题M8AS181如图3，商品条形码是商品的“身份证”，共有13位数字。它是由前12位数字和校验码构成的，其结构分别代表“国家代码、厂商代码、产品代码和校验码”。

其中，校验码是用来校验商品条形码中前12位数字代码的正确性的。它的编制是按照特定的算法得来的。其算法为：

步骤1：计算前12位数字中偶数位数字的和a，即a=9+1+3+5+7+9=34;

步骤2：计算前12位数字中奇数位数字的和b，即b=6+0+2+4+6+8=26;

步骤3：计算3a与b的和c，即c=3×34+26=128;

步骤4：取大于或等于c且为10的整数倍的最小数d，即d=130;

步骤5：计算d与c的差，就是校验码X，即X=130-128=2。

请解答下列问题：

（1）《数学故事》的条形码为9 787 534 546 47Y，则校验码Y的值为。

本题主要用来测试学生“感悟现实生活中数的意义”这一数学抽象具体表现的水平状况。本次测试中，本题的平均得分率为52.3%，数学总体能力处于A、B、C、D四个水平的学生在此题上的平均得分率分别为74.5%、37.0%、21.4%和6.7%。

对于这个测试结果，笔者认为，学生的阅读能力，尤其数学阅读能力的培养任重道远。在日常教学中，不乏这样的现象：教师为了节约课堂时间，不由自主地代替学生阅读，代替学生从“生活”中抽象出“数学”，快速进入“数学”，用数学知识解决生活问题，并美其名曰“提高课堂效率”。实际上，在“被代替”阅读的过程中，学生的阅读能力得不到培养，从而丧失了发展抽象能力的机会。

下面是笔者讲解一道应用题的实录：

（出示题目：某地区居民用电，按高峰时段与空闲时段规定了不同的单价。某户居民5月份高峰时段用电量是空闲时段用电量的两倍，6月份高峰时段用电量比5月份高峰时段用电量少40%，结果6月份的用电量和5月份的用电量相等，但6月份的电费却比5月份的电费少25%，求该地区空闲时段民用电单价与高峰时段民用电单价的比值。）

师 同学们默读题目两遍，有困难的同学举手。

（近一半学生举手。）

师 （对一位有困难的学生）困难在哪里？

生 题目太长，读不懂什么意思。

师 分解题目的表述：“某户居民5月份高峰时段用电量是空闲时段用电量的两倍”这句話能理解吗？可以通过什么方式表达这句话的数量关系？

生 能。可用字母a表示“5月份空闲时段用电量”。

师 你还能表示——

生 还能表示“5月份高峰时段用电量”“6月份空闲、高峰时段用电量”。可是还有电费单价、电费，弄不清关系。

师 当数量关系复杂时，可以通过什么途径将数量关系清晰地表达出来？

生 （齐）表格。

师 如何设计表格？

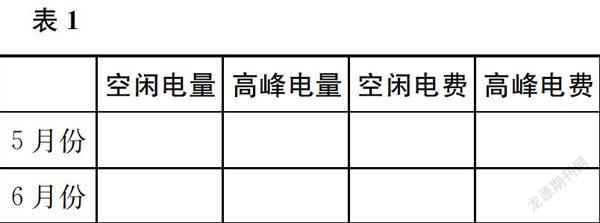
生 应该包括5月、6月，还有空闲用电量、高峰用电量、空闲电费、高峰电费等。

（该生在黑板上画出表1。）

（对于电费的表示，有部分学生又出现困难。）

生哦，对了，再用字母表示空闲时段和高峰时段的电费单价啊。

……

数学的信息常常“淹没”在复杂的问题情境与冗长的文字表述中。这里，教师耐心地教会学生分解信息，抽丝剥茧，舍去事物的“物理属性”得到数学的研究对象，并思考如何将研究对象之间的关系表达出来，让学生逐渐能在自然语言、符号语言、图形语言、表格语言之间自如地“穿行”。

此外，根据我们对学生就“数学抽象能力培养”的问卷题的调查结果可知，全省约有17%的教师给学生发展数学抽象能力的时间和机会不充裕或不够充裕。因此，教师应该把培养学生的数学抽象能力当作数学教学的“行动指南”之一，给足学生阅读、经历、体会的时间与机会，让学生对待周围的世界慢慢养成“用数学的眼光观察”的习惯，对待周围的事物慢慢形成“透过现象看本质”的本领。

参考文献：

[1]董林伟，喻平.基于学业水平质量监测的初中生数学核心素养发展状况调查[J].数学教育学报，2017（1）.