齿轮接触疲劳极限应力测试研究

杨小勇，薛亮

(陕西法士特齿轮有限责任公司，陕西西安 710077)

0 引言

齿轮接触疲劳试验因试件数量多、加工精度高、检测费用大、试验周期长等特点，试验费用昂贵和数据离散性大，因此得到一个准确的齿轮疲劳极限应力就尤为必要。目前相关资料文献中介绍的齿轮材料极限应力测试方法主要有S-N曲线图解法、少试验点法和升降法。本文作者通过某齿轮材料的接触疲劳强度测试，对3种测试极限应力的方法进行研究，从数据精确度结果来看优先推荐采用升降法，建议在熟悉该材料性能的条件下可以使用少试验点法，不建议使用S-N曲线图解法。同时证明了升降法测试可以通过数据稳定性检测法来有效减少齿轮接触疲劳试验点数。

1 3种方法介绍

1.1 少试验点法

大多数以实用为目的且对该齿轮材料性能和齿轮接触疲劳试验较为熟悉时，使用少试验点法(或称预试验法)预估疲劳极限应力，以便节约试验时间和试验费用。该方法通常选取3个应力级，每个应力级的试验点数不少于3个。最低应力级的试验点应均不越出。最终选取中间应力级的应力值作为疲劳极限应力值。

此次试验的齿轮属硬面齿轮，因此作者选择试验循环基数N0=5×107。同时根据经验(图1所示为渗碳淬火钢接触疲劳极限应力)，渗碳淬火钢的极限应力中值一般在1 500 MPa左右，应力级差Δσ一般选取5%σHlim左右。

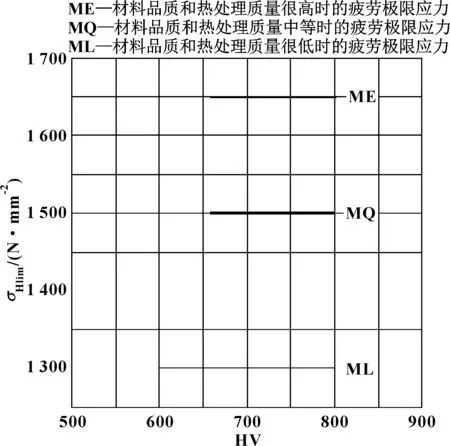
图1 渗碳淬火钢接触疲劳极限应力

根据表1，预估该材料的极限应力σHlim=1 358 MPa。

1.2 S-N曲线图解法

目前国内很多文献中都采用的成组法试验原理(把应力作为定值，将疲劳寿命作为随机变量)，将试验数据通过统计处理拟合出的形如Y=A+BX的回归方程直线，极限应力即为此直线方程中循环寿命为5×107时的应力值。图2即为根据此方法截出的该材料齿轮的接触疲劳极限应力，但是这个结果明显小于作者根据少试验点法做出的估计值(在1 358～1 424 MPa之间)。

表1 少试验点数据

注：F表示齿轮失效，N表示齿轮未失效，下同。

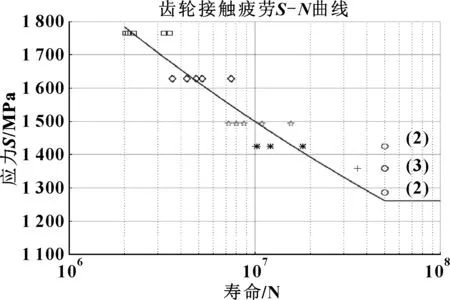
图2 50%可靠性的某齿轮接触疲劳S-N曲线

1.3 升降法

在进行升降法前，该齿轮要先进行强度校核，预计算疲劳极限应力值σHlim，然后在此值的上下附近，选取4～5个应力级进行升降法试验。应力级增量一般选取Δσ=5%σHlim左右。通常首个试件选高应力水平进行试验，确保试件在未达到循环基数前失效，这样既可减少试件的浪费，也可检验强度计算的准确性。当首个试件失效，第二个试件就在低一级应力下进行，反之就在高一级应力下进行试验，升降法的有效试验应从第一个转向点的前一个点开始算，且越出和不越出试验点数均不能少于5个。升降法试验数据如表2所示，统计数据如表3所示。

表2 升降法试验数据

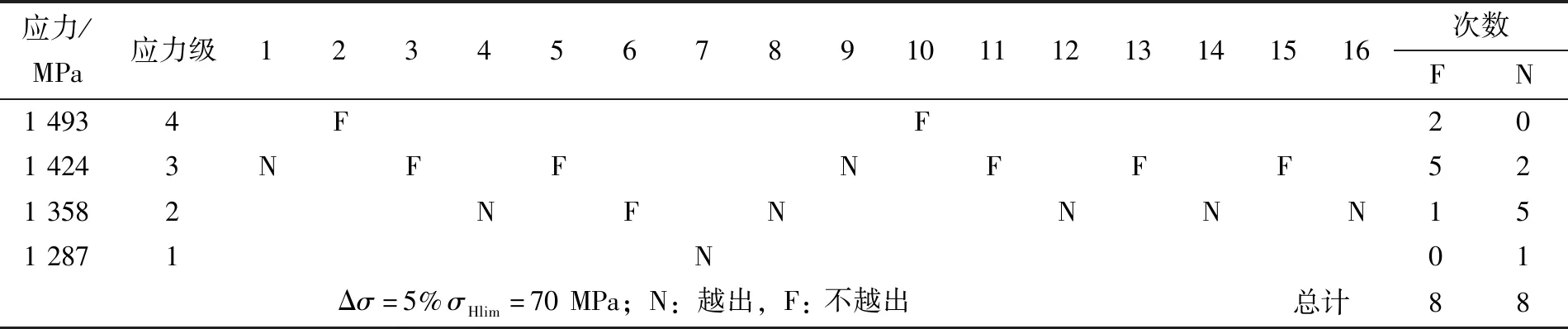
表3 采用升降法统计数据

然后采用BS3518标准推荐的迪克逊-姆德法(采用极大似然估计法推导，数据要求符合正态分布)处理试验数据，如表4所示。

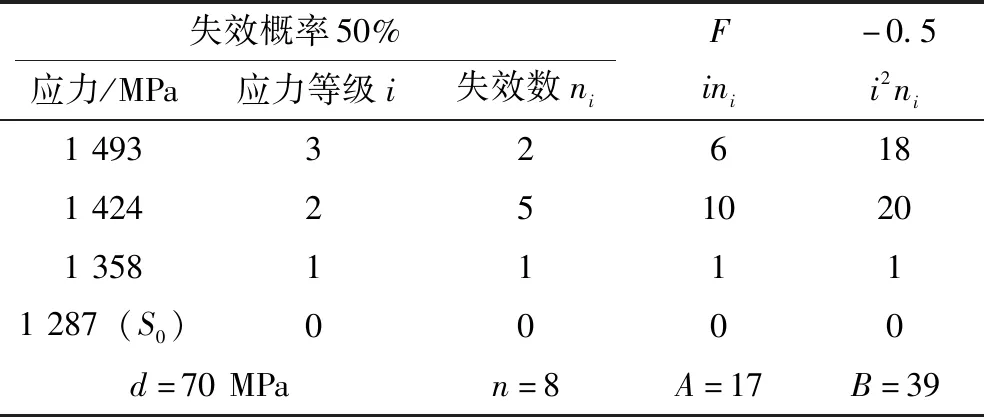
表4 采用迪克逊-姆德法处理数据

表中：n=∑ni,A=∑ini,B=∑i2ni。

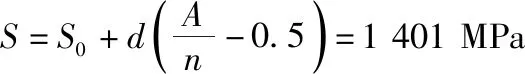
此应力值是失效概率为50%的齿轮接触疲劳极限。

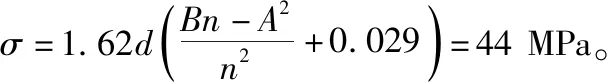
1.4 三种测试方法比较

三种测试方法的比较如表5所示。

表5 三种测试方法比较

原因分析：预试验法和S-N曲线图解法都是把应力作为定值，将疲劳寿命作为随机变量，但是齿轮接触疲劳强度试验有一个特点，低应力水平下疲劳寿命离散性很大，而且由于试验周期太长，不能进行充足数量的齿轮试验，因此测得的齿轮疲劳极限应力不够准确。而升降法是取定疲劳寿命，把应力作为随机变量，所以获得的试验数据中越出点数和不越出点数相差不大，这样就可以得到齿轮在疲劳极限附近的概率分布，从而得到具有统计特征的极限应力，因此升降法测得的极限应力值准确得多。

2 试验点数的研究

2.1 充足试件的迪克逊-姆德法和数据稳定性检测法比较

某齿轮弯曲疲劳升降法试验数据如图3所示。

图3 某齿轮弯曲疲劳升降法试验数据

(1)采用迪克逊-姆德法处理数据。

表6所示为采用迪克逊-姆德法统计处理数据。

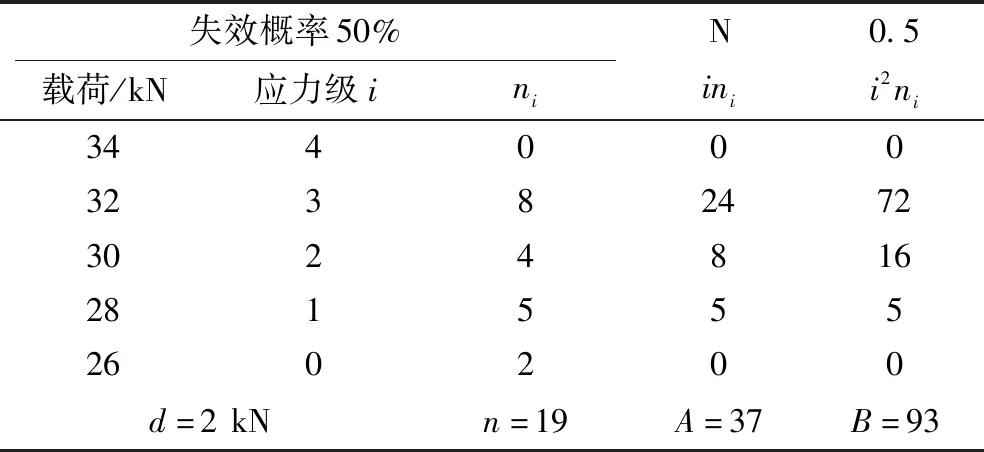
表6 采用迪克逊-姆德法统计处理数据

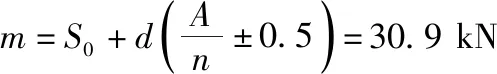
注：如果小概率事件是越出则使用加号，如果小概率事件是失效则使用减号。此处用加号。

此载荷是失效概率为50%的齿轮弯曲疲劳极限。

同时经过计算此数据中前20个试验点的FFlim=30.3 kN。

(2)采用数据稳定性检测法处理试验数据

升降法中的试验点数越多则计算出的疲劳极限应力值准确性就越高，但是受限于齿轮接触疲劳试验周期和样品数(一个试验点需用时30天，一对齿轮只能产生一个试验点)，所以在保证数据准确性的前提下，如何减少试验点数就很有必要。

如表7所示，可以采用数据稳定性检测方法(该方法同样要求数据符合正态分布)来判断：当有效数据达到10个以后(含第10个点)，即可进行数据稳定性检验，如果连续有4个试验点的稳定性误差满足下式要求，即可停止试验。

式中：Fn为在第n个有效数据点时以各应力水平上试验点数为权的加权平均值，可用下式计算：

表7 采用数据稳定性检测法统计处理数据

上式表示的加权平均值即可作为失效概率为50 % 、循环基数为N0的疲劳极限值，所以FFlim=30.9 kN。

这与迪克逊-姆德法得出的数据相同，同时将表6中前20个试验点的数据用两种方法进行统计比较后，数值也相同。而齿轮接触疲劳强度和齿轮弯曲疲劳强度的试验数据一般都是正态分布，因此可以通过数据稳定性方法来检测接触疲劳强度和确认有效的试验点数。

2.2 少试件时迪克逊-姆德法和数据稳定性检测法比较

将表2的齿轮接触疲劳升降法试验数据采用数据稳定性检测法处理，结果如表8所示。

表8 数据稳定性检测方法处理齿轮接触疲劳试验数据

出现连续4个稳定试验点时的σHlim=1 401 MPa这样的结果和采用迪克逊-姆德法得到的结果完全相同。若采用全部6个稳定试验点的σHlim=1 399 MPa，二者之间的偏差仅为0.15%。

通过以上齿轮弯曲和接触疲劳试验数据的统计结果，表明采用迪克逊-姆德法和数据稳定性检测法得到的齿轮疲劳极限值几乎相同。

3 总结

(1)齿轮接触疲劳试验优先推荐采用升降法，在熟悉该材料性能的条件下可以使用少试验点法，不建议使用S-N曲线图解法。

(2)通过处理试验点数足够多的齿轮弯曲疲劳试验数据和试验点数较少的某材料的齿轮接触疲劳试验数据，表明迪克逊-姆德法和数据稳定性检测法得到的齿轮疲劳极限值几乎相同，证明了数据稳定性检测法的准确性。

(3)升降法测试时，在试件数量有限时可以通过数据稳定性检测来节约齿轮接触疲劳试验点数，有效的试验点数最多可以缩减至14个。