信息技术在初中数学深度化教学中的应用研究

王梧 陈世萍

摘要：深度化教学是核心素养引领下的基本课堂教学策略之一。教师在初中数学课堂中应利用微课的先行组织者功能、内容整合功能，以及几何画板等，实施深度化教学，促进学生高阶思维能力的发展。

关键词：信息技术;初中数学;深度化教学

深度化教学是核心素养导向下的基本教学策略之一，是一种“使动性”的教学行为。深度化教学是以教师在课堂中引导学生深度学习、确立发展性教学理念、促使学生获得深度发展、实现课堂学习由表层走向内涵为特征的。初中数学课堂如何借助信息技术实施深度化教学策略？通过什么手段和形式将信息技术融合到数学课堂教学中才能实现深度化教学，达到对学生核心素养的有效培养？笔者在课堂教学实践中做了一些尝试。

一、充分发挥微课的先行组织者作用

深度化教学摒弃对知识点的表层化教学，反对死记硬背、机械训练，强调在教学中将学生置于知识产生的特定情境中。微课用时短，内容丰富，形式多样，且不受时间和空间的限制。因此，教师可以利用微课为学生创设丰富的学习情境。微课作为数学课上的先行组织者常发挥出出人意料的效果。

例如，无理数和实数的概念在沪科版教材中被安排在七年级下册“实数”一节中。由于无理数和实数是高度抽象的概念，学生在学习前缺乏生活和学习经验，因此这一内容一直被一线教师视为教学重点和难点。笔者在教学“实数”时，在课前利用微课向学生生动地展示数系理论发展的简史和希帕索斯发现      的故事，讓学生感知人类在认识数系的过程中并非一帆风顺，而是经历了种种曲折，以及人类愿意用生命来寻找、捍卫真理的精神。当学生面对无理数和实数这一新的学习任务时，他们原有的认知结构中缺少同化此新知识的上位观念。为此，笔者利用微课呈现了一个引导性材料，构建了一个使新旧知识发生联系的桥梁，激发了学生学习实数的兴趣，有效地突破了七年级学生学习无理数和实数这一新概念的困难。

二、利用信息技术实现学习内容的有机整合

多边形外角和定理在沪科版教材中被安排在八年级下册“多边形内角和”一节，教材对该定理的处理极其简单，将其作为多边形内角和定理的推论呈现出来。这样处理能突出多边形外角和与内角和的联系，使得知识的系统性和各章节的连贯性较强。我们认真分析该定理的结论，就会被它的优美奇妙所吸引，它反映了“多边形的外角和不依赖具体图形的形状和边数”，表达出数学研究亘古不变的一个主题——几何图形的不变性。我们再深入分析会发现多边形外角和的求法，集中体现了数学解决问题的思维方式，具有重要的思想方法上的意义。我们分析后发现沪科版教材安排的多边形内角和定理教学与该定理在课程中的地位是存在偏差的，难以有效地指导教师在课堂中进行深度教学和引导学生进行深度学习。

笔者在进行多边形外角和定理的教学时，对课本的呈现方式做了较大调整，在信息技术的支持下带领学生完成了定理的深度探究和证明。笔者利用一个动画：蚂蚁沿五边形爬行一圈回到原出发点，在爬行过程中连续转向360°，给学生创造了一种感性认识多边形外角和的情境，更启发学生认识到这个结论是一种逻辑推理。在合作探究环节，笔者利用几何画板制作了一个如图1所示的多边形外角向一点不断收缩成图2的Flash，最终这个多边形所有的外角经过收缩都“集中”在一起，形成如图3的周角。笔者利用几何画板演示多边形外角收缩的情景，让学生直观地感受到了“多边形外角和等于周角”。学生受Flash和“三角形外角和也是360°”的启示，思考后得出：可以通过叠加法来求多边形的外角和，其求法与三角形外角和的求法如出一辙。

通过信息技术的辅助，我们在数学课堂上可以将多边形的外角和定理与三角形的外角和定理的教学进行有机整合。学生通过几何画板的图形变换功能来探究多边形的外角和定理，能较为直观地获得结论。学生还将三角形外角和的求法自然地迁移过来，直观地将学习内容与原有的知识结构进行了顺应与同化，通过探究和证明，与原有的知识结构进行了融合，也有效地充实了课本中有关多边形外角和定理的学习。

我们在数学教学中不能简单地就事论事，应进一步利用信息技术较为便捷的探究图形的强大功能，来拓展、挖掘数学题背后所蕴含的指导学生发现、探究和证明的教育价值。

三、利用几何画板进行实验探究，促进构建反思

2018年广州市初中毕业生学业考试第25题因叙述文字简洁、图形简单，但问题设计巧妙、解题思路具有一定的技巧性而极具探究价值，备受初中生和中学一线教师的高度关注。为叙述方便，现将原题呈现如下：

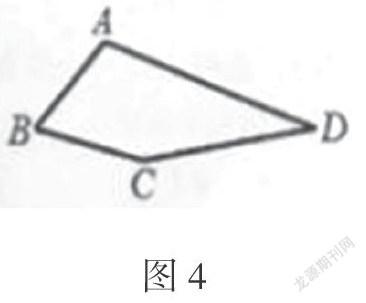
如图4，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC。

（1）求∠A+∠C的度数。

（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由。

（3）若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度。

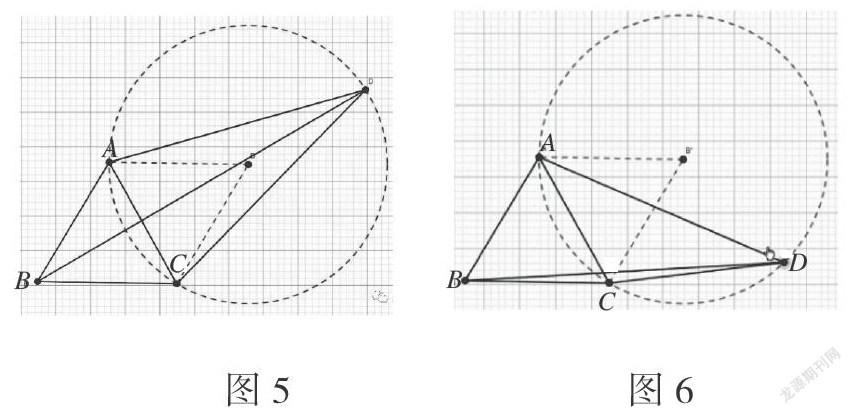
当我们读到∠B=60°，∠D=30°，AB=BC的条件时，稍加分析会发现，连接AC后会获得等边△ABC，再深入思考会在大脑中迸发出“定长定角”的直观反应，因此一个以AC为弦且弧AC为60°的圆被构造出来。在课堂中为了增加学生的直观印象，笔者利用几何画板演示了该结论，得到了图5。当保持∠D=30°这个条件不变时，学生在几何画板上利用鼠标拖动点D，会发现点D在构造的圆上运动，从而探究出点D不是定点，满足题意的点D的运动轨迹是一个圆，这极大地激起了学生的好奇心和探究欲。

该题第1问虽然简单易于解决，但它却为第2问的解决铺设了条件。根据等边条件的处理策略，第2问使我们联想到“等边式旋转”，可通过构造旋转型来尝试解决。当下，利用信息技术能很便利地实现旋转。其中几何画板可以很方便地构造旋转，且可以利用显示功能实现颜色标记，便于学生观察。我们可以利用几何画板构建如图7的旋转图形，利用几何画板的度量功能，我们很容易引导学生发现图7中△BDD′为等边三角形，∠DCD′=90°。此时的第2问在信息技术的支持下获得了解题的突破口，解题者只需逆着结论发现过程完成证明即可。当我们利用鼠标拖动点D改变△BAD的形状，会直观地发现△BCD′的形状随之改变，但度量的结果仍是△BDD′为等边三角形，∠DCD′=90°。当点D运动到如图9所示的劣弧AD上时结论仍然成立，从而更深层次地引导学生发现该结论具有相对的不变性，深化了学生对第2问条件设置的探索和对结论的认识。

第3问的技巧性较强，如缺乏探究工具的支持，学生的思维难以获得突破。但我们借力信息技术时，探究解题思路的过程就变得相对简单，思维也获得了着力点。我们利用几何画板探究后发现，点E在如图10的圆弧上运动，所以点E运动的轨迹是以点A′为圆心，BC为半径的圆在等边△ABC内部的圆弧长。究其原因，第3问中的题设条件AE2=BE2+CE2与第2问中的圆中动点D到等边△ABC的三个顶点的距离有着同样的关系，从而明确了解题思路。

深度化教学要求教师确立發展性教学理念，探讨促进发展的教学策略，由表层走向内涵。在2018年广州市初中毕业生学业考试第25题的教学中，笔者在课堂教学中就利用信息技术的支持，以发展性的教学理念带领学生进行深入探究，为学生积累了丰富的活动经验和探究技巧。笔者利用几何画板的度量和追踪轨迹功能，使学生从情境中获得个别规律，再从个别规律中抽象出一般规律，在生动有趣的探究活动中，降低了学习的难度，又增加了学习的深度。学生再次面临实际问题时，就可以将原型、理论迁移到实际问题中，从而达到高阶思维的认知水平。

四、实践思考

利用信息技术实现课堂深度化教学，能将“知识的课堂” 转变为“能力的课堂” ，最终实现“创新的课堂”，从“教师中心”到“以人为本，以学习为中心”，促进学生学习增值，打造为学生的终身发展服务的课堂教学模式。但需要注意的是，我们不能不加选择地滥用信息技术手段，依赖信息技术手段，而使信息技术变成了课堂教学的“统治者”，这样反而会出现教学上新的“错位”。利用信息技术实现课堂深度化教学，需要教师在课前认真分析学生的原有认知结构和教学生长点，以及传统课堂教学的疑难之处，将信息技术手段主要集中于认知结点发生强烈的冲突或疑难之处，借助信息技术的先进手段和强大功能引导学生深入探究，利用信息技术给学生创造真正属于他们思想交锋的角斗场，促进学生高阶思维能力的发展。

参考文献：

[1]高茂军.核心素养引领下的课堂教学革新[M].天津：天津教育出版社，2018.

[2]王永清.“先行组织者”教学模式在中职数控加工工艺教学中的应用[J].电子世界，2013（9）.

[3]广德宏.几何画板学习环境下的数学实验研究[J].上海中学数学，2012（6）.

（责任编辑：李晓杰）