高中数学解题能力的调查与研究

张健敏

摘 要：培养学生的数学解题能力，是提高学生数学成绩的关键。人们在学习数学和运用数学解决问题时，表现出来的各种思维过程和数学思维能力都是在解题的过程中培养和发展起来的，并通过解题得以呈现和展示。提高学生的数学解题能力是一项长期而艰巨的任务。只有在平时的练习中，有意识地培养学生从不同层次，不同角度，不同方向对问题进行分析，才能够拓展学生的思维层次，使他们的思维能力由单向性发展为多向性。

关键词：数学解题能力;思维能力;审题习惯;反思能力

美国著名心理学家G.波利亚曾经说过：“问题是数学的心脏，掌握数学意味着什么？那就是解题。”所以，培养学生的数学解题能力，是提高学生数学成绩的关键。

《高中数学新课程标准》明确指出，高中数学课程应注重提高学生的数学思维能力。人们在学习数学和运用数学解决问题时，不断的经历直观感知，观察发现，归纳类比，空间想象，抽象概括，符号表示，运算求解，数据处理，演绎证明，反思与构建等思维过程。这些过程是数学思维能力的具体体现。而这些思维能力又都是在解题的过程中培养和发展起来的，并通过解题得以呈现和展示。这更说明了解题能力的重要性。那么，现在的高中生，基本解题能力如何呢？对此问题，我在本校范围内进行了如下的调查分析。

关于高中生数学解题能力调查问卷

1.在做数学题目时，我能很快的投入到状态中。

A总是这样 B偶尔，有时候 C很少

2.对所学的数学基本概念，定义，定理公式等，我能够熟练掌握，并灵活运用。

A总是这样 B偶尔，有时候 C很少

3.在做数学题目时，能够明确出题者的意图，知道考的是哪些知识点。

A总是这样 B偶尔，有时候 C很少

4.在做数学作业前，或者每次考试前，能够把所学的相关知识或近期所学习的内容进行回顾和梳理。

A总是这样 B偶尔，有时候 C几乎从不

5.做题时，我会很快的把同它相近或者相关的知识点联系起来。

A经常这样 B偶尔，有时候 C几乎从不

6.通过解题，我能够把所学的知识进行整理，在头脑中形成整体性的知识网络。

A总是这样 B偶尔，有时候 C很少

7.在做数学题目时，只要找到某种方法，我就会毫不犹豫的进行下去。

A总是这样 B偶尔，有时候 C很少

8.在寻找解题思路时，做出一种方法后，我会力尝试其他方法，争取找到最简洁的方式。同时，对各种方法进行比较归类。

A一直这样做 B偶尔，有时候 C很少

9.每次数学考试后，我不仅改错，而且能够从自身和试卷两方面分析错因，进行纠错和整理。

A一直这样做 B偶尔，有时候 C很少

10.每次考试后，我都会对试卷上的知识点和考点进行归类，把握高考的考点和方向。

A一直这样做 B偶尔，有时候 C很少

11.每次考试后，我都会从自身情况出发，进行分析和反思，调整自己的学习策略，寻找更适合自己的学习方法。

A一直这样做 B偶尔，有时候 C很少

12.解数学题目时，当一种思路走不通，我会很快地从这个思路中走出来，从另外的角度思考问题。

A总是这样 B偶尔，有时候 C很少

13.对于自己曾经做过的题目，尤其是做错的题目，复习时我会有新的理解和发现。

A经常这样 B偶尔，有时候 C很少

14.我经常收集整理一些平时见过的或者老师说过的典型题，易错题或者我认为有价值的题目。

A一直这样做 B偶尔，有时候 C几乎从不

15.我能够将题目中的文字语言转化成函数表达式，表格或者图像。

A总是能够 B偶尔，有时候 C几乎从不

16.在数学题目中，我最喜欢的是

A基础题 B综合应用题 C探索提高题

17.我知道自己数学学习方面的优势和不足（包括学习内容，学习方法，个性特征等）

A很清楚 B有所了解 C不知道

18.我经常阅读数学课外读物和参考书，以提高自己等数学解题能力。

A经常 B偶尔，有时候 C几乎从不

这份调查通过问卷的形式对我校各年级的部分高中生进行了调查，了解到目前高中生數学解题能力方面的状况和存在的问题，力图寻找培养和提高解题能力的有效途径。试卷主要是通过学生在解题过程中的计划，评价，反思和自我调控等方面的情况来揭示学生解题能力的现状。

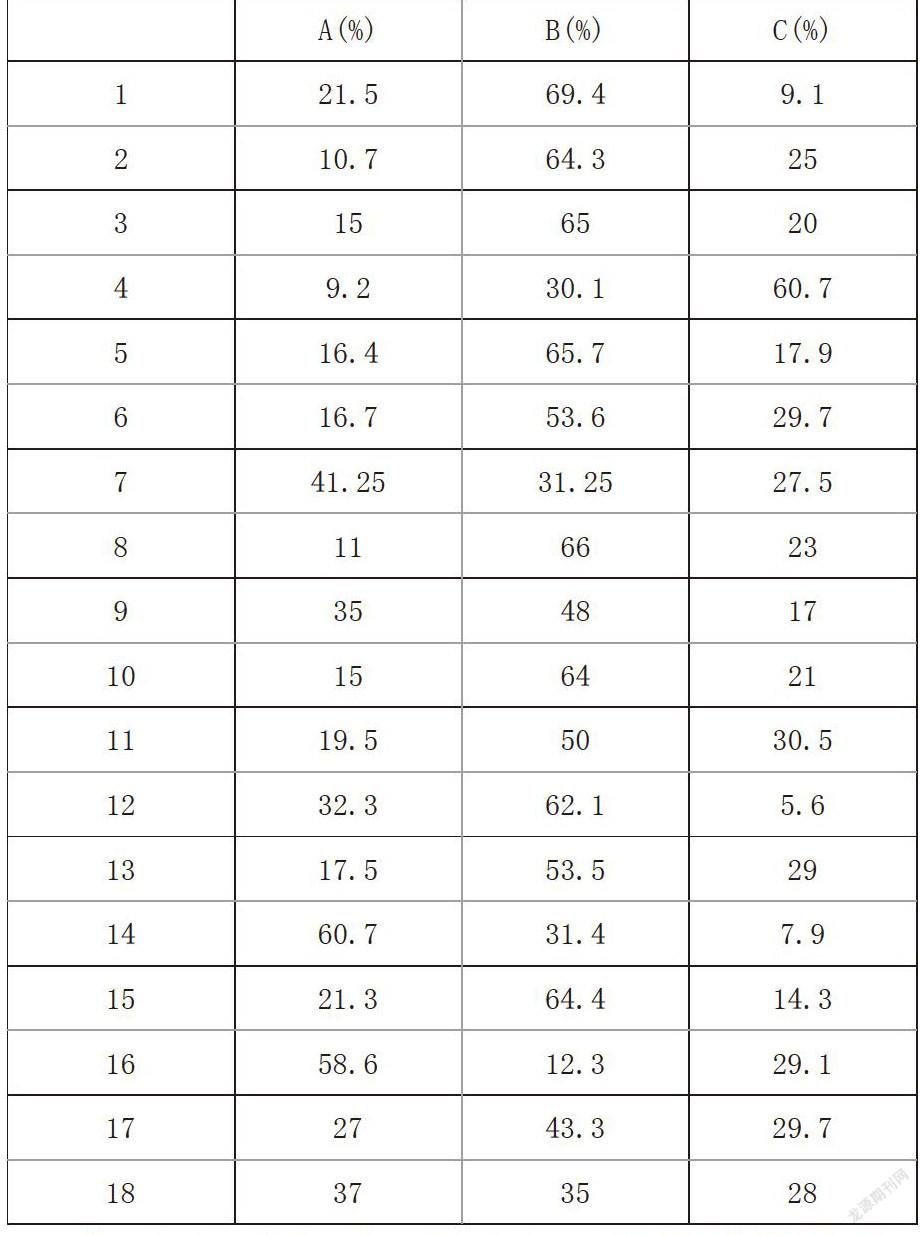
本次调查我随机选取了我校三个年级的部分学生，其中收回有效问卷高一151份，高二148份，高三131份，共计430份。其中男生228份，女生202份。调查结果如下

从上面的调查中，我们可以看出目前高中生数学解题能力的一些基本情况：

（1）学生的解题能力总体水平偏低，在能力的培养方面比较被动。在平时解题的过程中，只是单纯的做题，不能提升到能力的层面上来。

（2）从4，5，6题到调查结果中发现，学生不能对知识进行及时的复习和串联，不能将所学知识有机结合起来，形成完整的知识网络。知识在他们的头脑中都是章节性的或片段性的。所以在做综合题目时很有难度。

（3）只有11%的同学对“解题时，找出一种方法后，会力图寻找其他方案”回答“我一直这样”;15%的学生在“考试后会将试卷上的知识点，考点进一步，深层次的总结和剖析”回答“我一直都是这样”。“每次考试后，一直都会调整自己的学习策略和方法”的学生也仅有19.5%。17.5%的学生会在“回顾自己曾经做过的题目时，经常有一些新的认识和发现”。可见，目前高中生的数学解题能力不佳，积极主动的提高自身解题能力的意识和行为并不强烈。

（4）各年级学生在解题能力方面有明显的差异，高年级学生要好于低年级。在高三年级会有更多的学生“在做一道题目时，总是努力的尝试着探寻不同的方法。面对考试中的失败和不足，也总是能够进行总结和反思。”同时，高三学生文字语言转化成符号语言，函数语言，图像语言的能力也明显高于高一高二年级的学生。这表明知识的积累，能力的训练，习惯的培养对解题能力的提高是很有帮助的。

提高学生解题能力的对应策略。

（1）在平时的教学中，注重学生数学基础知识的掌握，基本技能的培养，以及知识结构的完善。

对于数学中的基本概念，性质，定理和公式等内容，教师在教学的过程中，不能粗枝大叶，一带而过，要深刻剖析它们的形成过程和推理依据。不仅要知道概念，定理的内容，更要掌握概念的内涵，知道为什么要引入这个概念，这个概念的本质特征是什么，该如何应用。例如数列，它的本质特征就是“以正整数集（或它的有限子集）为定义域的函数，是按照一定顺序排列的一列有序的数。

不仅如此，还要掌握概念的外延。例如，对于数列而言，还必须理解，数列又是一种特殊的函数，它蕴含着函数的本质和意义，所以要用函数的观点来看待数列，借助函数的研究方法来研究数列。从函数模型，连续与离散之间的关系的角度来认识数列，突出数列的本质。

例如：数列，求这个数列前30项中的最大项和最小项。

本题如果从代数角度来计算，计算量很大，对学生而言有很大的难度。所以可以从函数的角度来分析这个问题。若把它当作函数，利用函数的单调性来解决本例题。

=它在（0，）和（，正无穷）都是递减的.其图像类似双曲线，而数列是一种特殊的函数，定义域为N，所以它是函数上的一个一个孤立的点，约等于9.9。所以a9最小，a10最大。

（2）注重教材的作用，做好例题的示范性

有些教师在教学的过程中，对于教材中的例题往往一带而过，有时甚至完全否定，从另外的试卷或者参考书中选取他们认为更综合更经典的“有内容”的例题。觉得这些例题才更符合学生的实际水平，更能体现自己的特色。其实，这并不是明智之举。教材是众多专家经过多重思考，仔细斟酌，反复推敲，才最终编写出来的。具有科学性，示范性，典型性和导向性。事实上，高考试卷一直坚持“根在教材”的命题原则。很多题目，都是以书本上的题目为“原型”的。

当然，高考试卷中并不会出现原题，而是将课本中的一部分或几部分问题情景巧妙的结合在一起。从表象信息看不出什么，但其思想方法确是一致的。所以，教师应该最大限度的发挥教材的作用。认真分析教材中的典型例题，必要时进行变式练习和思维训练，促进“智慧技能”与“技能性思维”的形成。同时，也使学生对课本更加的重视。

（3）形成良好的审题习惯。

审题是发现问题的前提，认真审题是快速且正确的答题的基础，是提高数学成绩的基石。有很多学生能力还是不错的，但是由于习惯不好，审题粗心，在平时的作业甚至是考试中，总有很大的失误，严重影响数学成绩。所以，在平时的数学学习中，教师必须长期且有意识地对学生进行审题能力的培养，使学生逐渐形成良好的审题习惯。

（4）增强检验意识，提高反思能力。

学生在解题时，不仅要审题细致，对其结果还要有一个检验的意识。做完一道题目，不能草草结束。应该给自己一个短暂的缓冲时间，对其结果进行核查，验证，做好全面的检验工作，避免遗漏问题的出现。这样，可以在很大程度上降低做题的出错率。

只有這样，才能防止学生的学习停留在例题的表层。引导学生对知识进行正确且合理的迁移，才能使学生的解题能力和思维品质得到更高层次的提升。

在解题的过程中，将复杂的知识简单化，将简单的问题一般化，才能找到问题的根源，透过现象看到问题的本质。从而达到举一反三，触类旁通的效果。才能真正达到做一题，会一类，通一片。从而让学生在探究中感受到数学的实用性和美妙性。

提高学生的数学解题能力是一项长期而艰巨的任务，只有在平时的练习中，有意识地培养学生从不同层次，不同角度，不同方向对问题进行分析，才能够拓展学生的思维层次，使他们的思维能力由单向性发展为多向性。让学生在解题过程中获得乐趣，产生灵感，悟出正确的思路和方向，从根本上提高学生的数学解题能力。

参考文献

[1]沈正洲.浅谈数学导学案的编制与运用《数学大世界》.[J].2010年（3）：31

[2]曹军.《数学教学参考》.[J].2015年第1-2期

[3]杨云.《高中数学教与学》.[J].2013年第8期