浅谈小学数学应用题的教学

凌铁中

摘要：数学学科教学要有文化意义、思维意义、价值意义，即要有人的意义。小学数学是培养小学生逻辑思维能力和分析综合能力的主要学科，对小学生的发展具有重要意义。应用题作为数学问题中的一个重要组成部分，因其信息量大，变化莫测而时常让学生感到头疼，因此教师应积极探索行之有效的教学方法，帮助学生做好应用题。

关键词：小学数学 应用题教学方法 数学思维模式 数学智慧

数学学科的教学不仅是为了让学生获得若干知识、技能和能力，同时也是为了生成与提升人的精神、思想情感、思维方式、生活方式以及价值观。也就是说，数学学科教学要有文化意义、思维意义、价值意义，即要有人的意义。

小学数学是培养小学生逻辑思维能力和分析综合能力的主要学科，教好小学数学首先要掌握小学教材教学的全部内容，明确各章节的目的要求，也就是教学任务。要抓好小学基础知识的教学，对数的认识、概念、大小比较、四则计算、混合运算、简便计算、应用题的类别和解题方法这些基础知识，教师要教扎实、教牢靠。

同时，要抓住小学数学文字应用题的重点。由于这些题目变化莫测，教师要反复讲解、精心指导，培养学生的应变能力，让学生掌握解题技巧。要结合小学生的文化知识水平制订切实可行的教学计划，做到因人施教、因材施教。在长期的教学实践中，笔者针对数学应用题采用了以下几种教学方法，现详述如下，以供大家参考。

1.比方法

农村低年级的学生由于对某些应用题涉及的事物性能、特征、作用、价格等不够理解，从而影响他们的计算。教师要将学生数学学科思维方式的培养提升到学生长远发展的高度来加以认识，要注重对学生独立、独特、个性、新颖的思维和想象力的培养。这时，采用打比方的方法进行教学是一个很不错的选择。

例1：（1）有航母3艘，是潜水艇的2倍少1艘，在水面航行的艘数多还是在水底航行的艘数多？

解题时学生不知道哪种船在什么地方航行，我们就把鸭子比作航母、鱼儿比作潜水艇，学生就一目了然了。

（2）古代一人在街上卖矛和盾，来一客官问买一只矛多少钱。这人回答说，一只矛和一块盾为一套，共14文钱，买2只矛的钱可以买5块盾（用替代法算）。

学生对古代的矛和盾从未见过，我们就把刺刀比作矛、铁板比作盾。这一比方使学生对矛和盾的形状、作用、价格有了初步了解。

2.趣味法

兴趣是最好的老师，利用有趣的数学题，调动学生数学学习的积极性，从而能积极引导学生自主学习。改变数学课堂以知识讲授为任务的平淡乏味的教学模式，让数学课堂变得精彩，这样学生们就会积极主动、乐此不疲地发现问题、分析可题、解决问题，而不是枯燥、机械、反复地强调，培养了他们分析和解决问题的能力。

例2：父子俩到体育馆一个圆形沙池旁，步测周长求面积。父亲先行一步，儿子踩着父亲起点的脚印前进，当他俩分别到终点时脚印与起点时的脚印相重合。父亲数了一下，周围一共60个脚印，重叠的脚印只算一个;儿子测量，自己每步走48厘米，父亲每步走64厘米。提示：距离一定，步子的长短与步数成反比例。0.64∶0.48=4∶3，0.64×3=0.48×4=1.92，也就是说，爸爸走3步，儿子要走4步。爸爸走3步3个脚印，起点的脚印暂时不算，到最后再算。儿子走4步，第4步的脚印与爸爸第3步的脚印重合。也只见到3个小脚印，3+3=6，60÷6=10，1.9210=19.2，19.2÷3.14÷2=3，3.14×32=28.26

3.演示法和图示法

有些数学问题用文字描述让人难以理解，这时我们根据物体特征抽象出几何图形，或者便于自己理解的图形。利用图形描述和问题分析，可以把复杂的数学问题变得明确形象，有助于探索解决问题的思路，可以帮助学生直观地理解数学，在整个数学学习过程中发挥重要作用。因此，演示法和图示法是很好的选择。

例3：（1）剪2个完全一样的三角形和2个完全一样的梯形，分别拼成平行四边形，从而用平行四边形的面积公式推出三角形和梯形的面积公式。

（2）准备一个圆柱體和一个等底等高的圆锥体，把圆锥体装满沙子倒入圆柱体，3次倒满，从而用圆柱体的体积公式推出圆锥体的体积公式。

通过（1）（2）的演示，学生懂得每种图形的面积或体积公式是如何得来的，并能熟悉公式。

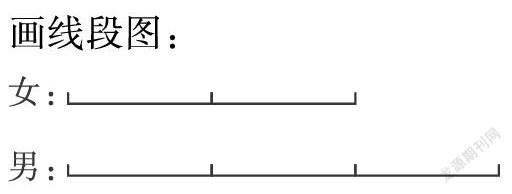
（3）五（1）班有学生40人，其中女生的一半与男生人数的1/3一样多，男女各多少人？画线段图：

从图中可以看出，女生占全班的2/5，男生占全班的3/5。

4.画图助解

例4：一个长方形周长16厘米，以这个长方形的每条边为边长向不同方向画4个正方形，4个正方形的面积和是65平方厘米。求长方形的面积。

把左边和上边的正方形去掉，把右下角补上，这样四边都是由长和宽组成，可知16÷2=8。因为这个四边形左上角是长方形的角，是直角，所以它是正方形，可得8×8=64。这个大正方形是由2个小正方形，也就是4个正方形的一半（65÷2=32.5）和两个面积相等的长方形组成，得（64-32.5）÷2=15.75，得到长方形的面积。如果老师一时想不出画图助解的方法，可以用高一级知识来解。设长方形的长为x，2x2+2（8-x）2=65（16÷2=8）。解这个方程，每解一步推出一道算式。x2+（8-x）2=32.5，推出65÷2=32.5;2x2+64-16x=32.5，推出（8×8=64）;2x2+31.5-16x=0，推出64-32.5=31.5;x2+15.75-8x=0，推出32.5÷2=15.75。解得x1=4.5，x2=3.5。解方程推出的算式与画图助解的算式一模一样，所以对推出的算式进行分析，就能得到画图助解的方法。以后老师凡是暂时想不出的算法，都可以用高一级知识来解，解的途径不同，推出的算式有相同的，也有不同的，这些不同的都是它们的解。

5.方程法和倒推法

数学思维模式是多种多样的，小学生也需要掌握数学的逆向思维，通过理解并运用符号表示数、数量关系和变化规律，使用符号可以进行运算和推理，得到结论，从而建立符号意识。这是进行数学表达和数学思考的重要形式，列方程和倒推法是一个很好锻炼学生逆向思维的方法。

例5：（1）停车场停了27辆汽车，其中货车是客车的2倍还多3辆，客车有多少辆？

用算术法27-3=24，24÷（2+1）=8学生难以理解;设客车为x辆，x+2x+3=27，这样学生就容易理解了。方程左边表示什么，右边同样也表示什么，也就是说等式两边表示的内容相同。例题中左边表示两车相加是多少，右边表示两车的总数。

（2）一位老太太用篮子提鸡蛋到街上去卖，第一次卖掉篮中鸡蛋的一半加半个，第二次又卖了篮中的鸡蛋的一半加半个，第三次还是卖了篮中的鸡蛋的一半加半个，这时篮子里还剩下13个鸡蛋。这位老太太一共提多少个鸡蛋去卖？

这道题由于单位1多次发生变化，学生不易掌握。我们就用倒推法来解：如果第三次半个不卖，就剩下13.5个，正好是一半，即（13+0.5）×2=27（第二次剩下的），则（27+0.5）×2=55（第一次剩下的），得（55+0.5）×2=111（全部）。

6.公式法

数学中有些数量关系是固定的，学生通过数与数量、数量关系、运算结果估计等方面的感悟建立数感，有助于理解现实生活中的意义。数量之间关系来回变换，可以增强学生思维的灵活性，展现出数学中变与不变之美。理解或表述具体情境中的数量关系，可以使学生的数学感知能力得到提升，从而增强学生学习数学的信心。

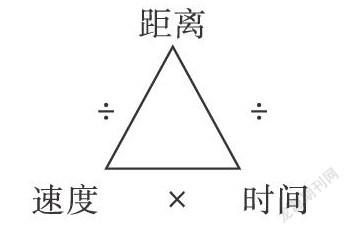
例如行程问题。距离÷速度=时间。

说明：三角形每条边表示算式，相对应的角表示“=”，如速度×时间=距离。

7.假设法

假设推理能力的培养应贯穿于整个数学学习过程。推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果;演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算。在解决问题的过程中，两种推理功能不同，相辅相成：合情推理用于探索思路，得出结论;演绎推理用于证明结论。假设法的运用可以拓展学生的数学思维方式，使学生感受数学的魅力。

例6：作马、板凳共33个，100只脚在地上站，作马、板凳各几个？（注：作马是过去木匠锯树用的三脚架）

解法①，假设全部是作马;解法②，假设全部是板凳。

例7：古代算术“鸡兔同笼”问题：数头15个，脚46只，鸡兔各几只？

解法①，假设全部是鸡：2 15=30，46-30=16，16÷2=8;解法②，假设全部是兔：4 15=60，60-46=14，14÷2=7。

例8：一只无盖圆柱体铁皮水桶，表面积为78平方分米，半径和高的比是2∶5，求底面积。半径和高没有实际长度，假设半径是2分米，高就是5分米;假设半径是1分米，高就是2.5分米。

解法①，设底面积为x平方分米;解法②，设半径为x分米。

8.分析法和综合法

苏霍姆林斯基说过：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者，而在儿童的精神世界中，这种需要特别强烈。”儿童这种与生俱来的探索欲望，是小学数学教学中实施探究性学习的重要基础。教师应该改变传统的教学思想和教学组织形式，多为学生创设自主探索的机会，还要给学生自主探索的时间和空间，让学生能真正有效地去探索，从而促使学生主动学习。分析法和综合法是学生自主学习的好方法，这两种方法无所谓已知到未知还是未知到已知，关键是找中间问题，所谓中间问题就是教学中的解答计划。

例9：有水牛8头，比黄牛多3头，是黑牛的2倍。三种牛一共多少头？

①黄牛多少头？8-3=5。②黑牛多少头？8÷2=4。③三种牛一共多少头？8+5+4=17。列综合算式的方法，首先看第二步，如果第二步有第一步的得数，把得数去掉，换上算式。如果第二步没有第一步得数，就看第三步，把第一步得数去掉，换上算式。上述算式把5去掉换上（8-3），把4去掉换上（8÷2）就是综合算式。

9.多解法

美国教育学家克罗韦尔指出：“教育面临的最大挑战，不是技术，不是资源，不是责任感，而是去发现新的思维方法。”思维方式可以是人的认识定式和认识运行模式的总和，也可以是个体思维层次（深度）、结构（类型）、方向（思路）的综合表现，是一个人认知素质的核心。多解法可以提升学生的思维能力，拓宽学生的思维模式，让学生体会数学学习的乐趣，提高学生学习数学的积极性。

例10：有红花和黄花7朵，红、蓝花10朵，黄、蓝花13朵。三种花各多少朵？用10种方法计算（指分步算式）。提示：①（7+10+13）÷2;②（7+10-13）÷2;③（7+13-10）÷2;④（10+13-7）÷2;⑤（10-7+13）÷2;⑥（13-10+7）÷2;⑦（13-7+10）÷2;⑧[7-（13-10）]÷2;⑨[10-（13-7）]÷2;⑩[13-（10-7）]÷2）。

10.问答法

创新意识的培养是现代数学教育的基本任务，应体现在教与学的过程之中，学生自己发现和提出问题是创新的基础。教师要改变“一言堂”的教学模式，讓学生成为课堂的主人，自己则充当课堂的组织者、领导者。问答法在笔者的数学课堂中就得到了很好的运用，学生主动地参与到课堂之中。在师生的一问一答中，学生的数学思想之花在课堂中得到精彩的绽放。

例11：今天中午狂风暴雨，再过32小时天空会不会出太阳？

例12：欢欢说，今年我虚龄16岁，但我出生以来只过了三次生日。这话是她什么时候说的？

11.归类法

数学问题千万种，为何讲几个例题就能解决大部分的题目呢？笔者认为，这是因为数学知识之间有各种联系，问题之间也就有各种联系。所以在学习中，我们要让学生学会将知识和问题归类，让教师的“授之以鱼”变成“授之以渔”，让学生的学习能力得到更好的发展。

求甲是乙的几倍、几分之几、百分之几、几比几、几成、几折、多百分之几、少百分之几，这8种问题可归成一类。前面所求的叫分率，靠近分率的叫标准量或单位1（特殊的分析后再定），标准量前面是比较量，比较量和标准量中间常有是、占、相当、比等词连接。这类题目的计算方法：①比较量÷标准量=分率。②已知条件中多百分之几、一加百分之几、少百分之几、一减百分之几。③按文字题中的公式法解。

例13：一根竹子三分之一插入水中，另一根竹子插入同样深的水中，露出的部分是第一根竹子露出部分的三分之一。第二根竹子长2.5米，第一根竹子长多少米？（用第①种方法解）

例14：一双皮鞋360元，比一双运动鞋便宜10%，比一双保暖靴贵20%，保暖靴比运动鞋便宜百分之几？（用第②种方法和第③种方法解）。

数学是打开神秘宇宙的钥匙。学数学不仅是学书本知识，更重要的是学思考方法和方式。我国著名数学家华罗庚曾这样说过：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之送，日月之繁，无处不用到数学。”当今数学的应用更是无处不在。数学就像一条神奇的纽带把各学科知识联系在一起，数学智慧就是生活的智慧。数学的美丽与神秘吸引着很多人不断去探索它的奥妙。因此在教学中，教师应当积极探索有效的教学方法，带领学生走进数学世界的大门，解决各种各样的难题，领略数学之美。

参考文献：

[1]何月丰.浙江省海盐县实验小学教育集团[J].小学数学教师，2017：78.

[2]范艳华.学生发展核心素养视域下的课堂教学指南：小学数学[M].长春：东北师范大学出版，2017.