MULTIPLICITY OF POSITIVE SOLUTIONS TO A CLASS OF MULTI-POINT BOUNDARY VALUE PROBLEM∗†
2019-09-05BaoZhaoYunruiYangYonghuiZhou
Bao Zhao,Yunrui Yang,Yonghui Zhou
(School of Math.and Physics,Lanzhou Jiaotong University,Lanzhou 730070,Gansu,PR China)
Abstract In this paper,an existence criterion of multiple positive solutions to a class of nonlinear multi-point boundary value problem is established by using the Guo-Krasnoselskii’s fixed-point theorem.At the same time,an example is also included to testify our conclusion.
Keywords positive solutions;multi-point boundary value problem;fixed point
1 Introduction
Boundary value problems for ordinary differential equations have extensive applications in the fields of physics,chemistry,biology and so on.For example,the deformations of an elastic beam in elastic mechanics can be modeled by a fourth order boundary value problem.In the past decades,based on some fixed point theorems[1–4],the lower and upper solutions method[5]and some degree theories[6],the existence of positive solutions to boundary value problems for fourth-order and higher order[2–5,7–12]has been always the focus of investigation,especially the existence of multiple positive solutions.In 2003,Ma[2]and Li[3]established the existence and multiplicity of positive solutions to some fourth-order boundary value problems,respectively.Recently,Zhou[11]investigated the existence and multiplicity of positive solutions to a fourth-order three-point eigenvalue problem by the Guo-Krasnoselskii’s fixed-point theorem.For other meaningful results,one can be referred to[7,9–11].
In 2014,by using a fixed point theorem on cone and combining with the constant variation method,Kong[12]obtained some results on the existence of at least one positive solution to the following fourth-order multi-point boundary value problem containing parameters
But to the best of our knowledge,there are not any results on the multiple positive solutions to the boundary value problem(1.1).Motivated by the ideas from literatures[2,3,11],our purpose in this paper is to investigate the multiplicity of positive solutions to(1.1),where α is a positive number,0<η<1 satisfies αη<1,λ>0 and ρ is a parameter satisfying 0<ρ<.
This paper is organized as follows.In Section 2,we introduce some preliminaries.In Section 3,we state and prove the main result on the existence of multiple positive solutions to(1.1).At the same time,an example is also included to testify the obtained results.
2 Preliminaries
For convenience,we first state some definitions,notations and preliminary results.Throughout this paper,we make the following assumption:
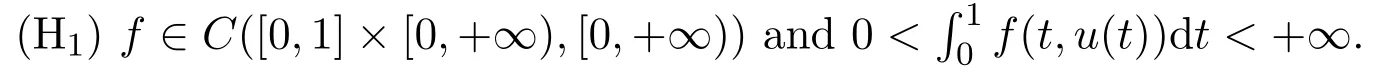
Definition 2.1[12]If a function u(t)satisfies the BVP(1.1),u(t)∈ C3[0,1]∩C4[0,1],and u(t)>0 for any t∈(0,1),then the function u(t)is said to be a positive solution to the BVP(1.1).
Theorem 2.1[1](Guo-Krasnoselskii’s fixed-point theorem)Let E be a Banach space,K ⊂ E be a cone in E.Assume that Ω1and Ω2are bounded open subsets of E with 0∈ Ω1and⊂ Ω2,and let T:K ∩(Ω1)−→ K be a completely continuous operator such that either
(i)∥T u∥≥ ∥u∥,u∈ K ∩ ∂Ω1and ∥T u∥ ≤ ∥u∥,u ∈ K ∩ ∂Ω2;or
(ii)∥T u∥ ≤ ∥u∥,u∈ K ∩ ∂Ω1and∥T u∥ ≥ ∥u∥,u∈ K ∩ ∂Ω2holds,then T has a fixed point in K∩(Ω1).
Let C[0,1]be endowed with the maximum norm

Let G1(t,s)and G2(t,s)be the Green’s functions of the following boundary value problems
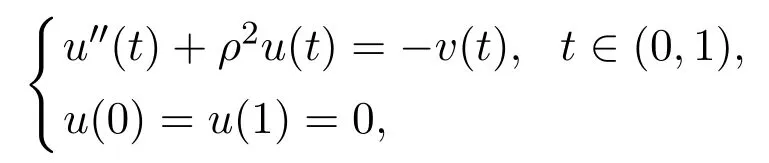
and
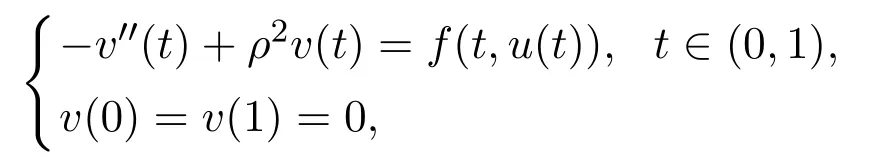
respectively.In particular,
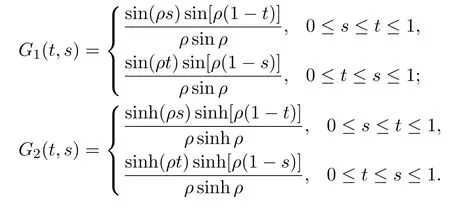
For any s,t∈[0,1],it is easy to check that
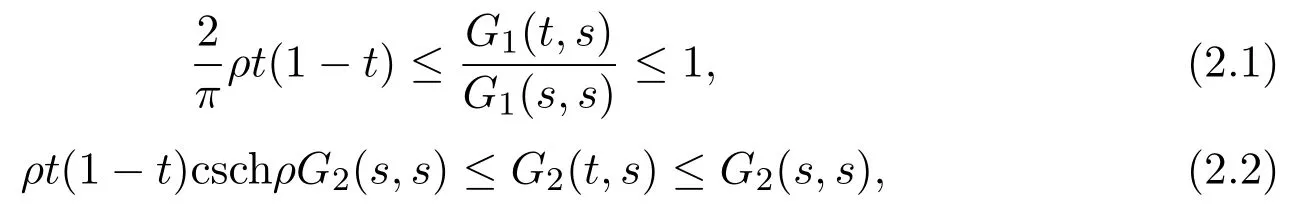
Denote C+[0,1]={u∈C[0,1]:u≥0}and define a cone K in C+[0,1]by
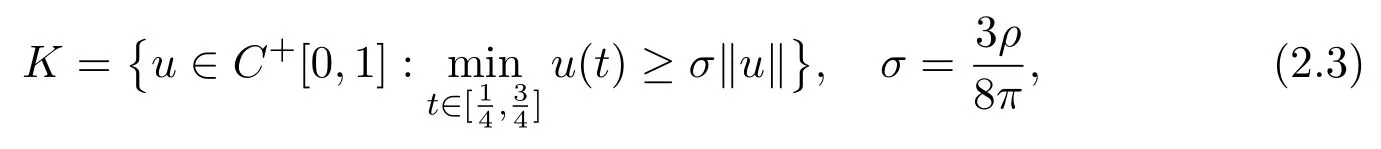
and denote
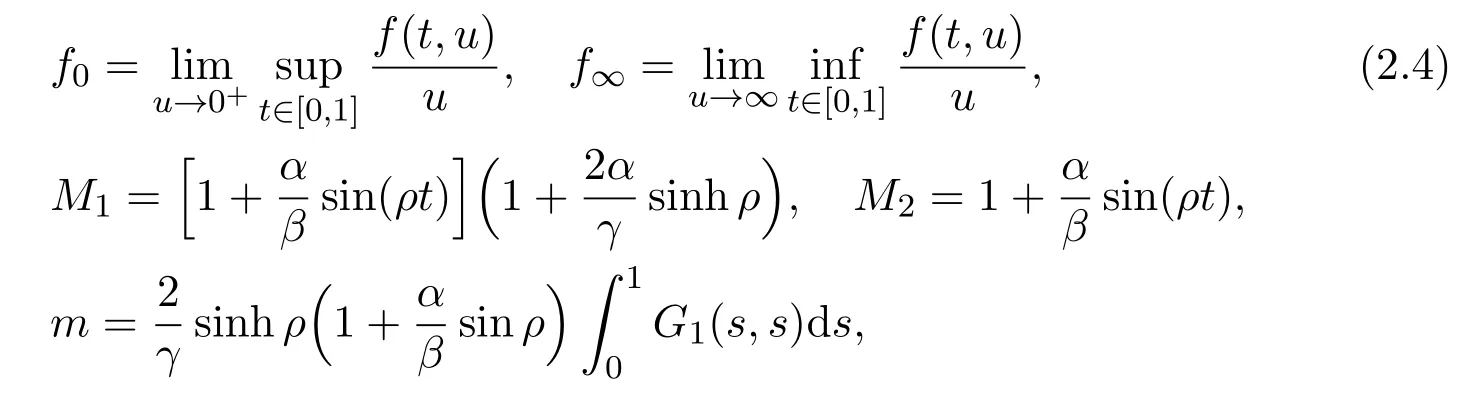
Define an integral operator T:K→C+[0,1]by
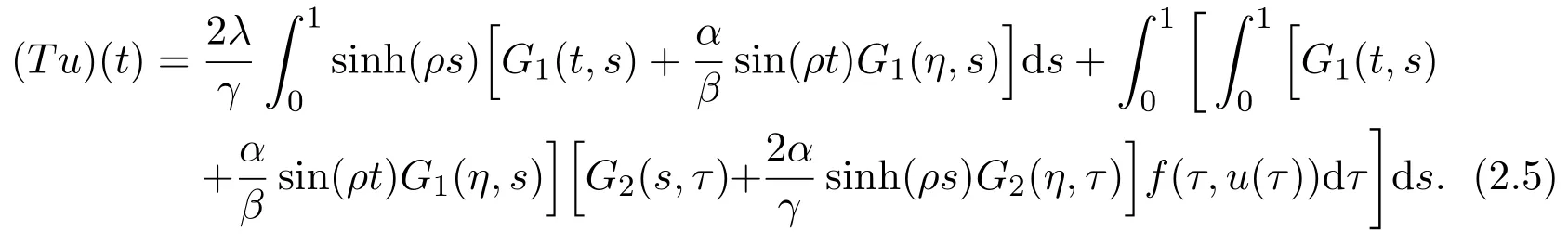
Obviously,u(t)is a solution to the BVP(1.1)if and only if u(t)is a fixed point of the operator T.
Lemma 2.1[12]Assume that(H1)holds,then T:K−→K is completely continuous.
Lemma 2.2Suppose that(H1)holds,then for the operator T:K −→K,the following conclusions hold:
(i)If f0=0,R1>0 is small enough,then ∥T u∥ ≤ ∥u∥ for any u ∈ K with∥u∥ =R1;
(ii)if f0= ∞,R1>0 is small enough,then ∥T u∥ ≥ ∥u∥for any u∈ K with∥u∥ =R1;
(iii)if f∞=0,R2>0 is sufficiently large,then ∥T u∥ ≤ ∥u∥for any u ∈ K with ∥u∥=R2;
(iv)if f∞= ∞,R2>0 is sufficiently large,then∥T u∥ ≥ ∥u∥for any u∈ K with ∥u∥=R2.
Proof(i)If f0=0,from(2.4),there exists a number R1>0 satisfying 0≤u≤R1such that f(t,u)≤εu,where ε>0 satisfies

Then we can choose a positive number λ0satisfying λ0m ≤R1.
For any t∈[0,1],u∈ K,∥u∥=R1,by(2.1),(2.2)and(2.5),we have
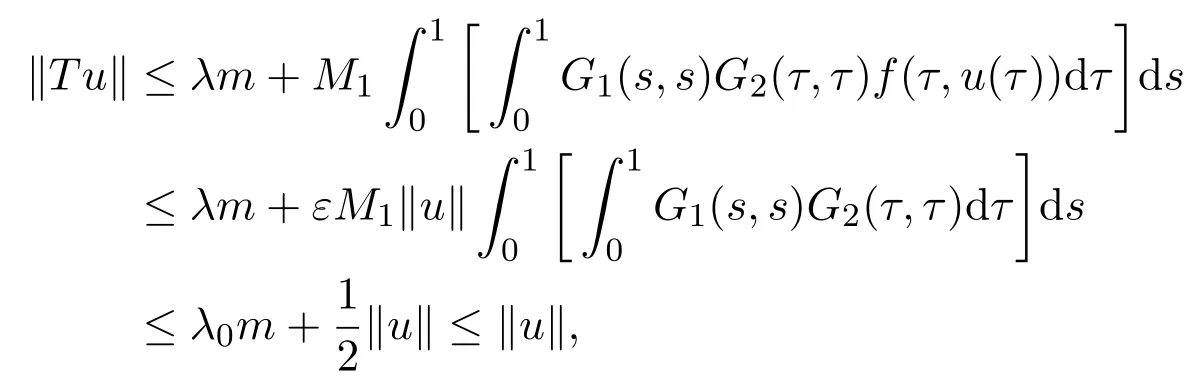
where λ ∈ (0,λ0].That is,∥T u∥ ≤ ∥u∥.
(ii)If f0=∞,from(2.4),there exists a number R1>0 satisfying 0≤u≤R1such that f(t,u)≥µu,where µ>0 satisfies
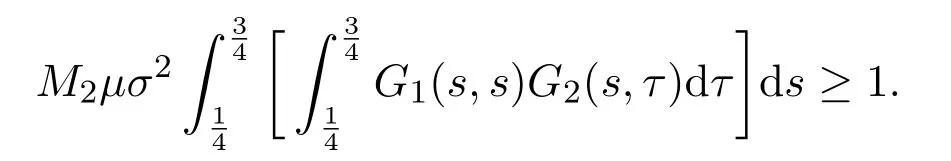
For any t∈[0,1],u∈ K,∥u∥=R1,by(2.1),(2.2)and(2.5),we have
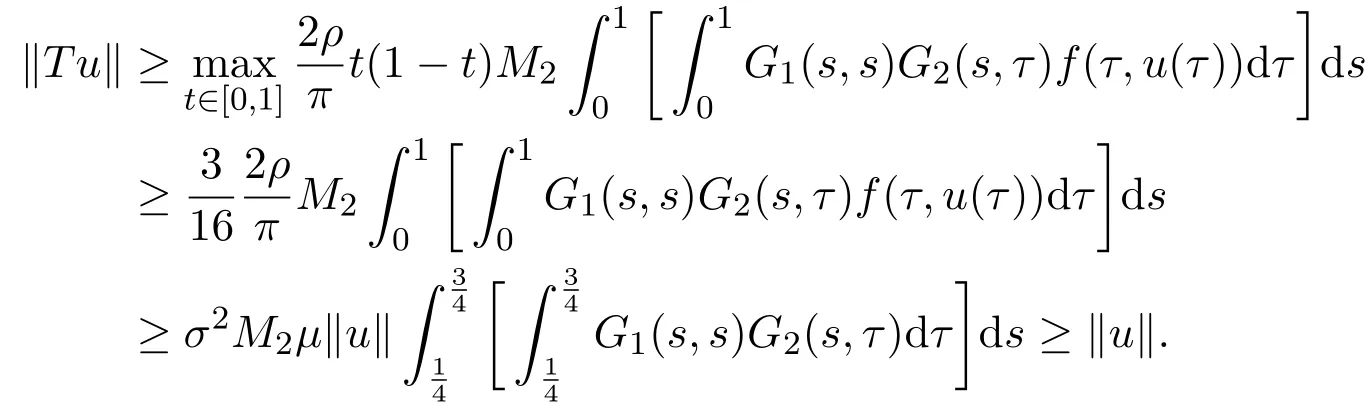
That is,∥T u∥ ≥ ∥u∥.
(iii)If f∞=0,from(2.4),there exists a number H>0 satisfying u≥ H such that f(t,u)≤ ε u,where ε>0 satisfies
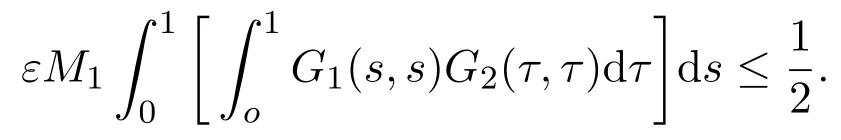
Thus,we consider the following two cases:
Case 1If f(t,u)is an unbounded function,let R2>max{R1,H}such that f(t,u)≤f(t,R2)for any t∈[0,1]and u∈(0,R2].Choose a positive number λ0satisfying λ0m≤R2.
For any t∈ [0,1],u∈ K,∥u∥=R2.By(2.1),(2.2)and(2.5),we have

where λ ∈ (0,λ0].
Case 2If f(t,u)is a bounded function,there exists a number N>0 such that f(t,u)≤N for any t∈[0,1]and u∈[0,∞).Let
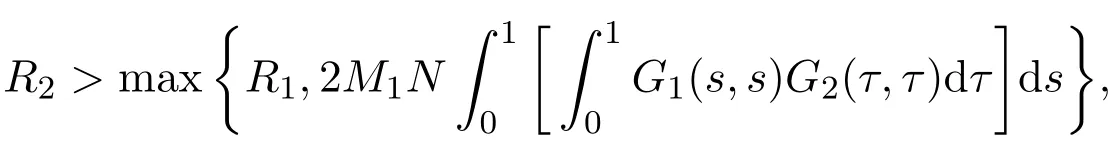
and choose a positive number λ0satisfying λ0m≤R2.
For any t∈ [0,1],u∈ K,∥u∥=R2,by(2.1),(2.2)and(2.5),we have
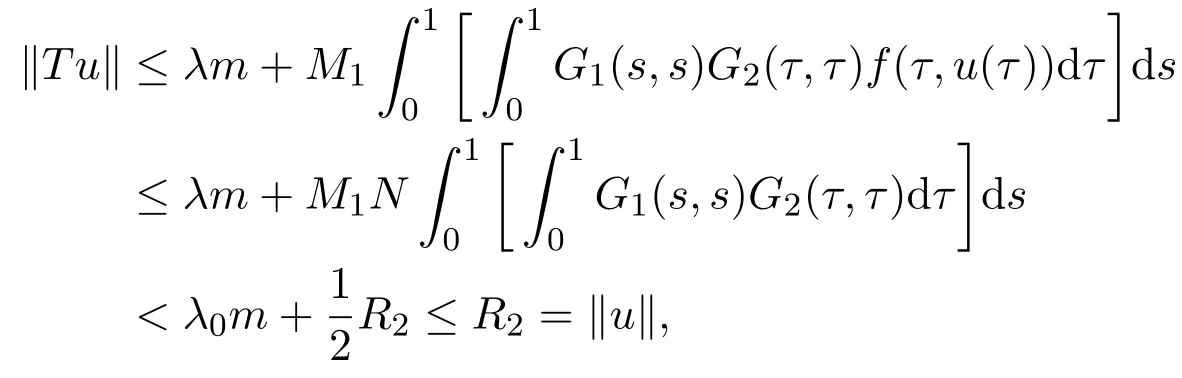
where λ ∈ (0,λ0].Therefore,∥T u∥ ≤ ∥u∥.
(iv)If f∞=∞,from(2.4),there exists a number r>0 satisfying u≥r such that f(t,u)≥µu,where µ>0 satisfies
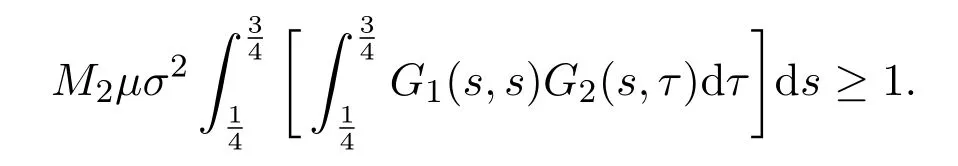
Let R2>max{R1,}.
For any t∈ [0,1],u∈ K,∥u∥=R2,we getu(t)≥ σ∥u∥= σR2>r.By(2.1),(2.2)and(2.5),it follows that
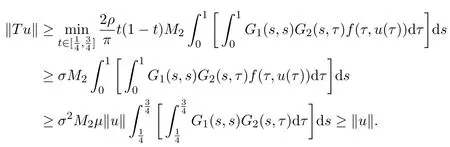
That is,∥T u∥ ≥ ∥u∥.The proof is completed.
Lemma 2.3[12]Suppose(H1)holds.Furthermore,f satisfies either
(i)f0=0,f∞=∞;or
(ii)f0=∞,f∞=0,
then the BVP(1.1)has at least one positive solution u=u(t).
3 Main Results
In order to establish the multiplicity of positive solutions to the BVP(1.1),we further make the following assumptions:
(H2)There exists a positive number R0>0 satisfying R0≪R1≪R2such that f(t,u)≥ k1R0for any t∈ [0,1]and u ∈ [σR0,R0],where

(H3)There exists a positive number R0>0 satisfying R0≪R1≪R2such that f(t,u)≤k2R0for any t∈[0,1]and u∈[0,R0],where

Theorem 3.1Suppose(H1)holds.If one of the following two conditions holds:
(i)Under(H2),f0=0 and f∞=∞ hold;
(ii)Under(H3),f0=∞and f∞=0 hold,
then the BVP(1.1)has at least two positive solutions.
Proof(i)Let E=C[0,1],Ω1={u∈ E:∥u∥ Choose Ω0={u ∈ E:∥u∥ Therefore,∥T u∥≥ ∥u∥,u ∈ K ∩ ∂Ω0. By Theorem 2.1,the BVP(1.1)has two positive solutions u1∈ K∩(Ω0)and u2∈ K∩(Ω2Ω1).Therefore Together with Lemma 2.3,it follows that the BVP(1.1)has two distinct positive solutions u1and u2. (ii)Let E=C[0,1],Ω1={u ∈ E:∥u∥ where λ ∈ (0,λ0].Therefore,∥T u∥ ≥ ∥u∥,u ∈ K ∩ ∂Ω0. Applying Lemma 2.3 again,it follows that the operator T has two fixed points u1∈K∩(Ω0)and u2∈ K∩(Ω1)satisfying(3.1),which are the two different positive solutions to the BVP(1.1).The proof is completed. Example 3.1Consider the following boundary value problem where ρ=1,α=1,λ=1,0<η<.Then,for any t∈[0,1],it is not difficult to obtain where Thus,we consider the following two cases: Case 1For f=u2,by(2.4),we have Choose such that f(t,u)≥ σ2R20≥ k1R0for any t∈ [0,1]and u ∈ [σR0,R0].Then Theorem 3.1(i)guarantees the existence of two positive solutions to the BVP(3.2).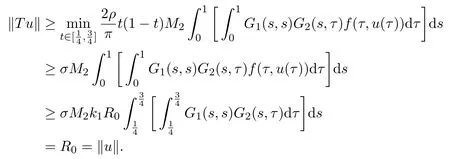


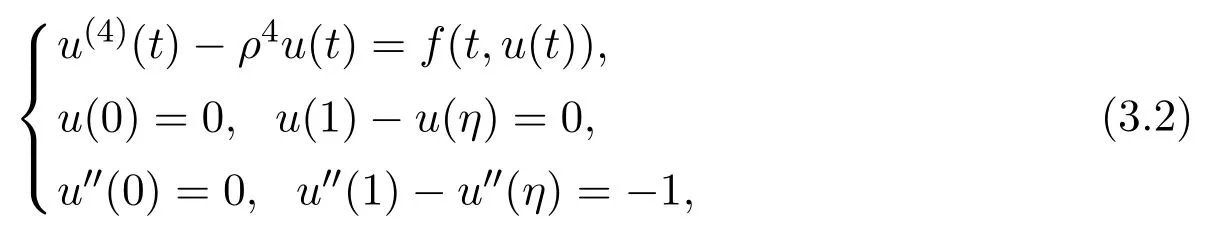
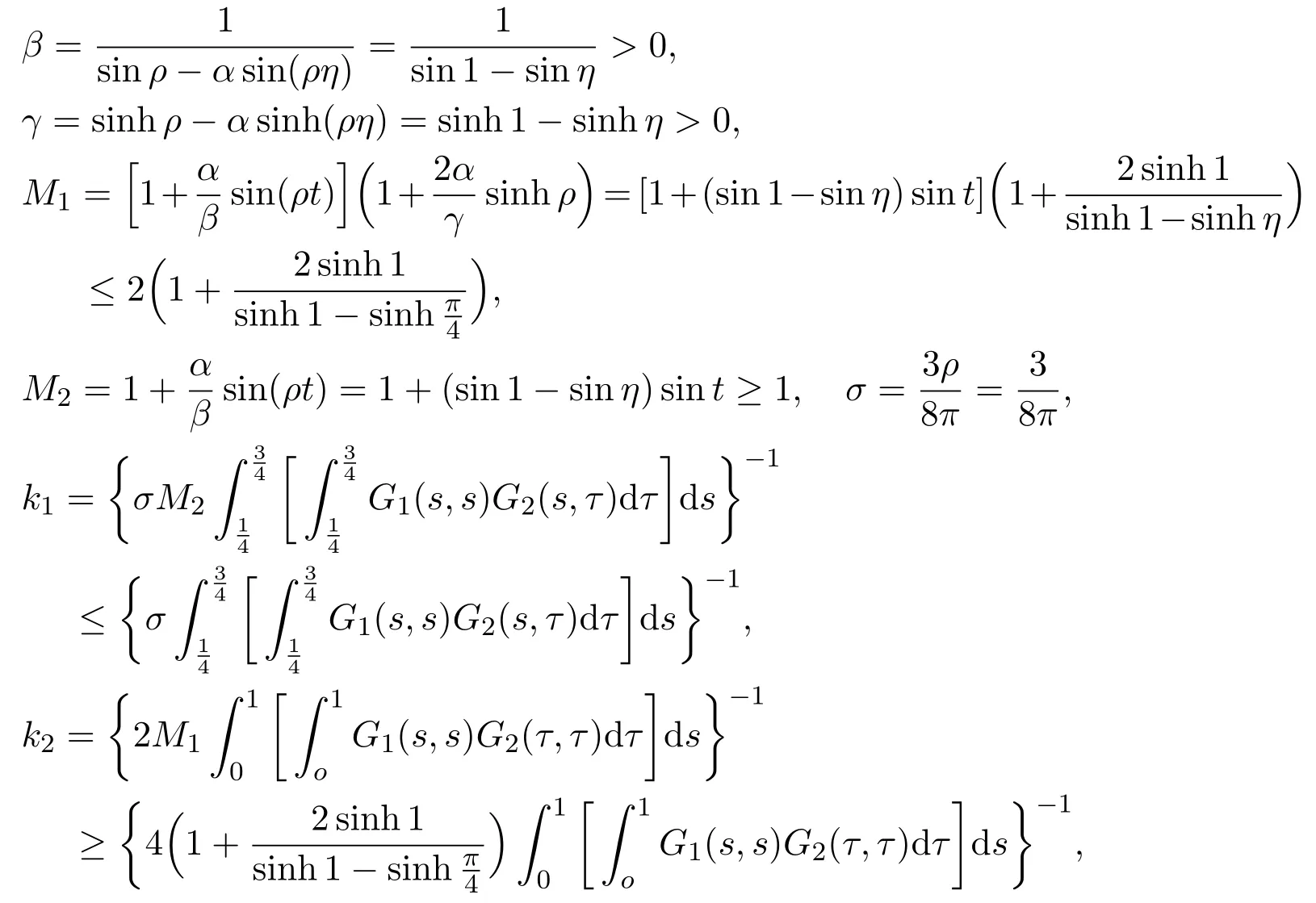
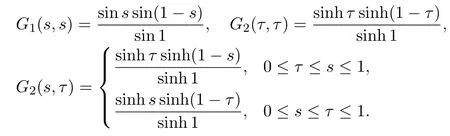
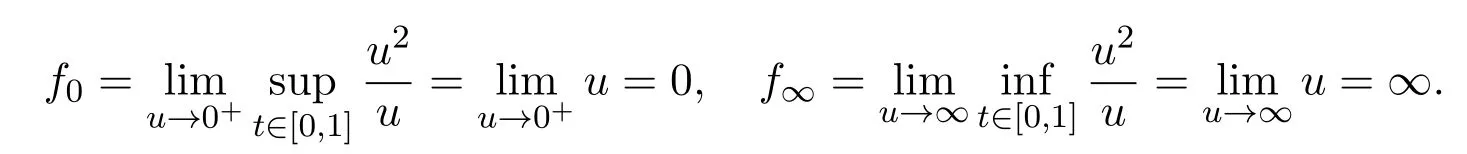
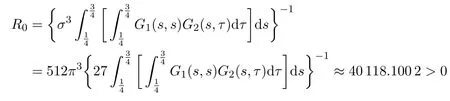
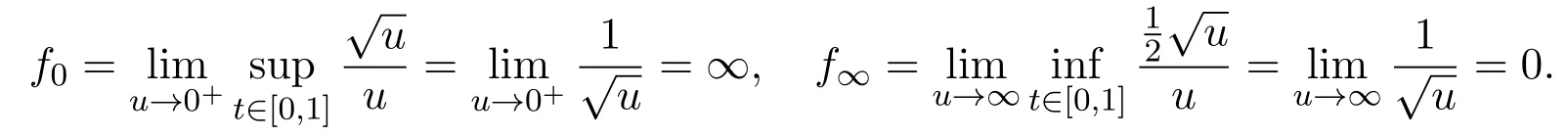
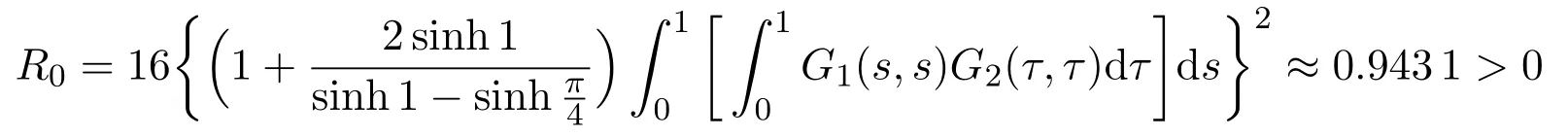
杂志排行
Annals of Applied Mathematics的其它文章
- SOME PROBLEMS IN RADIATION TRANSPORT FLUID MECHANICS AND QUANTUM FLUID MECHANICS∗
- THE QUALITATIVE ANALYSIS OF A TWO SPECIES AMENSALISM MODEL WITH NON-MONOTONIC FUNCTIONAL RESPONSE AND ALLEE EFFECT ON SECOND SPECIES∗†
- NOTE ON THE STABILITY PROPERTY OF THE VANISHING EQUILIBRIUM POINT OF AN ECOLOGICAL SYSTEM CONSISTING OF A PREDATOR AND STAGE STRUCTURE PREY∗†
- A BLOW-UP RESULT FOR A CLASS DOUBLY NONLINEAR PARABOLIC EQUATIONS WITH VARIABLE-EXPONENT NONLINEARITIES∗†
- ASYMPTOTIC EIGENVALUE ESTIMATION FOR A CLASS OF STRUCTURED MATRICES∗†
- THE CAUCHY PROBLEMS FOR DISSIPATIVE HYPERBOLIC MEAN CURVATURE FLOW∗†
