A BLOW-UP RESULT FOR A CLASS DOUBLY NONLINEAR PARABOLIC EQUATIONS WITH VARIABLE-EXPONENT NONLINEARITIES∗†

Qingying Hu,Donghao Li,Hongwei Zhang

(Dept.of Math.,Henan University of Technology,Zhengzhou 450001,Henan,PR China)

Abstract This paper deals with the following doubly nonlinear parabolic equations,where the exponents of nonlinearity r(x),m(x)and p(x)are given functions.Under some appropriate assumptions on the exponents of nonlinearity,and with certain initial data,a blow-up result is established with positive initial energy.

Keywords doubly nonlinear parabolic equations;variable-exponent nonlinearities;blow-up

1 Introduction

LetΩ be a bounded domain in Rnwith a smooth boundary∂Ω.We consider the following initial boundary value problem

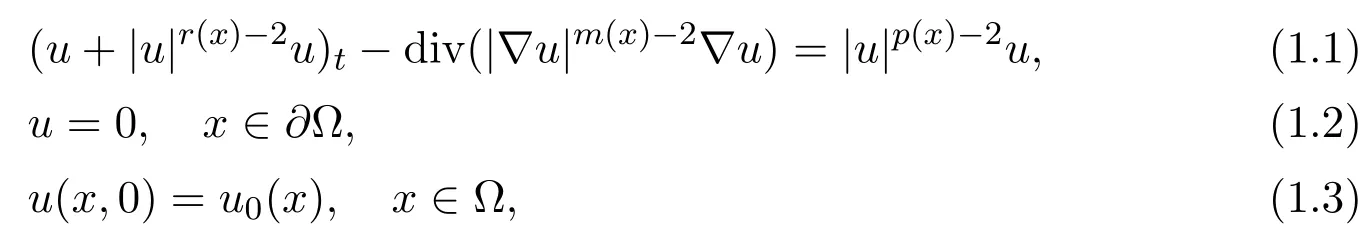
where the exponents m(·),p(·)and r(·)are given measurable functions on Ω satisfying

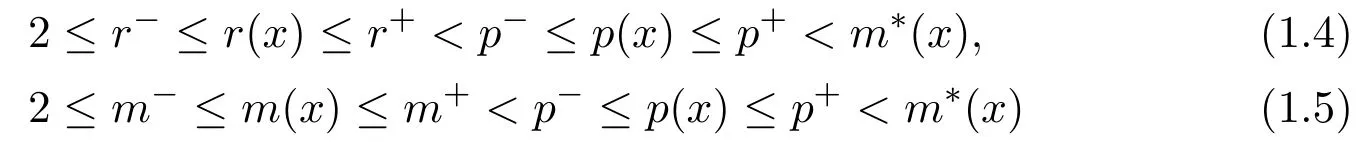
with

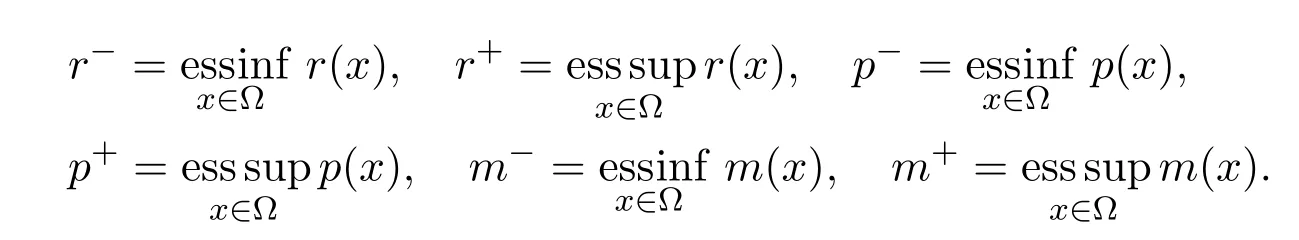
The exponent function m(x)satisfies

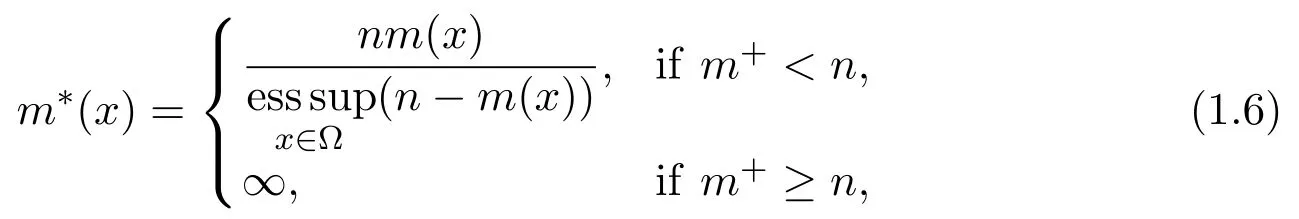
and the exponent functions m(x),p(x),and r(x)also satisfy the log-Holder continuity condition

where A ≥ 0,0< δ<1.The term ∆m(·)u=div(|∇u|m(x)−2∇u)is called m(·)-Laplacian.

Problem(1.1)-(1.3)has been widely used in many mathematical models of various applied sciences such as thin liquid films,flows of electro-rheological fluids etc.The interested readers may refer to[1-3]and the further references therein.

In case of constant-exponent nonlinearities(that is the exponents m(·),p(·)and r(·)are constants),the local,global existence,nonexistence and long-time behavior for problem(1.1)-(1.3)have been established by many authors,see,e.g.,[4-10]and the further references therein.

In recent years,the research on parabolic equations,elliptic equations and hyperbolic equations with nonlinearities of variable-exponent has been an interesting topic.For more results,see the recent papers[11-13].For problem(1.1)-(1.3),the authors in[1-3]applied Galerkin method to establish the existence of a solutions.But there are seldom works on blow-up of solutions.In this paper,we intend to find sufficient conditions on m(·),p(·),r(·),and the initialdata for which the blowup occurs.Our result extends that established in[5]from constant-exponent nonlinearities to variable-exponent nonlinearities.

The present work is organized as follows.In Section 2 we present some notations and materials needed for our work while in Section 3 we are devoted to proving our main result.

2 Preliminaries

In this section,we present some notations and materials needed for our work.Firstly,we give some preliminary facts about Lebesgue and Sobolev spaces with variable-exponents(see[17-19]).Let p:Ω → [1,∞]be a measurable function(see[17-19]).We define a Lebesgue space with a variable exponent p(·)by

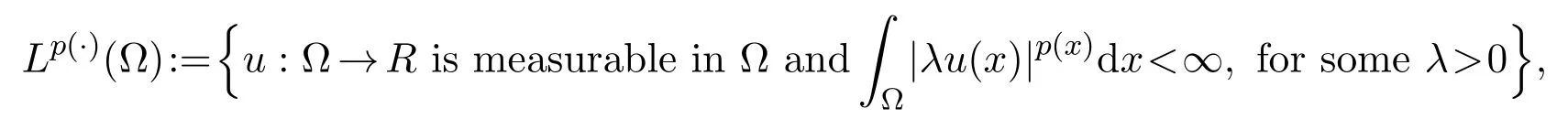
with the following Luxembourg-type norm

then Lp(·)(Ω)is a Banach space(see[19]).The variable-exponent Sobolev space(Ω)with p(x)∈ [p−,p+]⊂ (1,∞)is defined by:

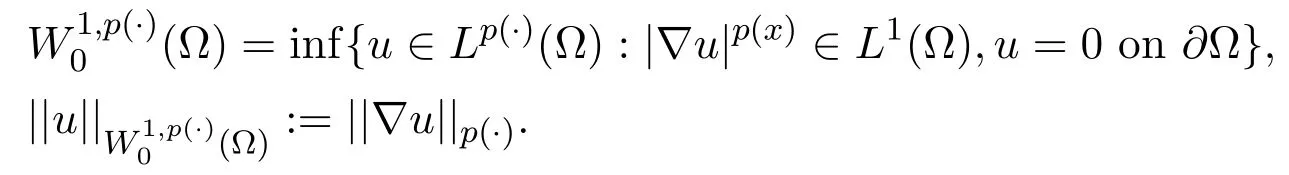
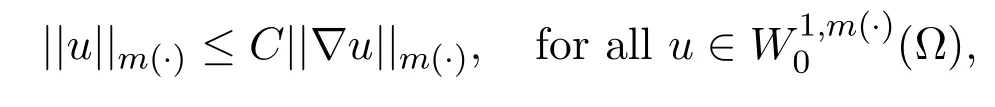
where C>0 depends on m(·)and Ω and the embeddings

are continuous and compact.

Proposition 2.1[5]Suppose thatΦ(t)∈ C2([0,T])satisfies

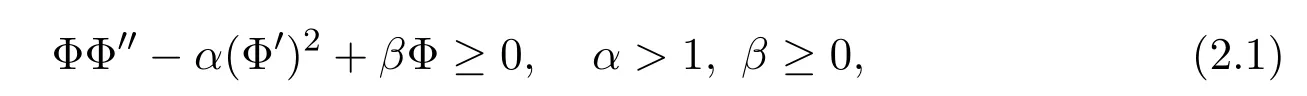
and

then the estimate of life span of the solution is given by

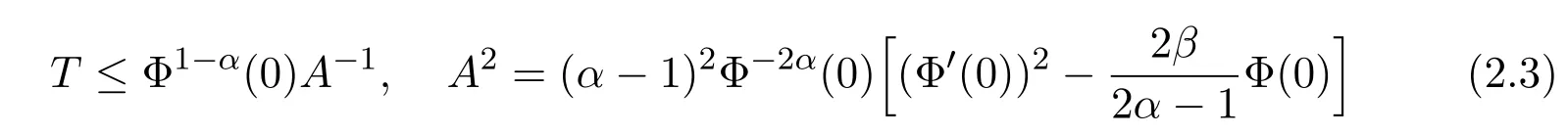
3 Blow-up

The authors in[1-3]established the local existence of solution by applied Galerkin method.In this section we state and prove our main blow-up result.

Theorem 3.1Let assumptions(1.4)-(1.7)hold and u0(x) ∈(Ω).If the initial data satisfies

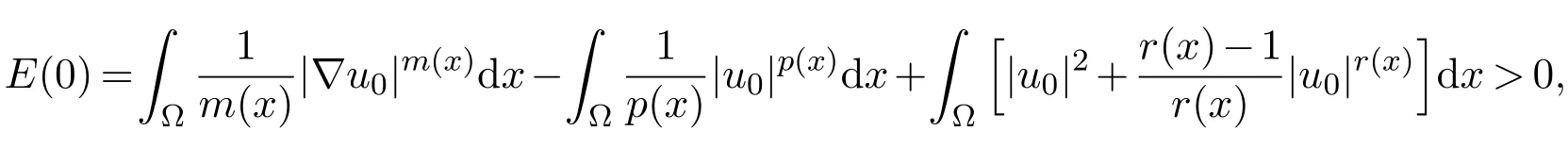
then there exists no global-in-time solution of problem(1.1)-(1.3)and the following estimate holds

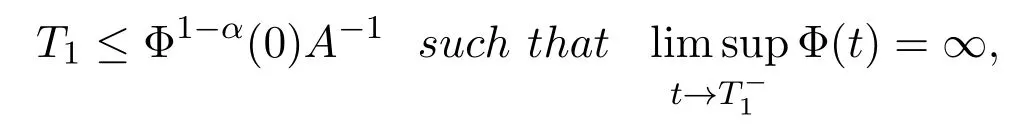
where A is defined as the same in(2.3),α =,β =p−E(0),and

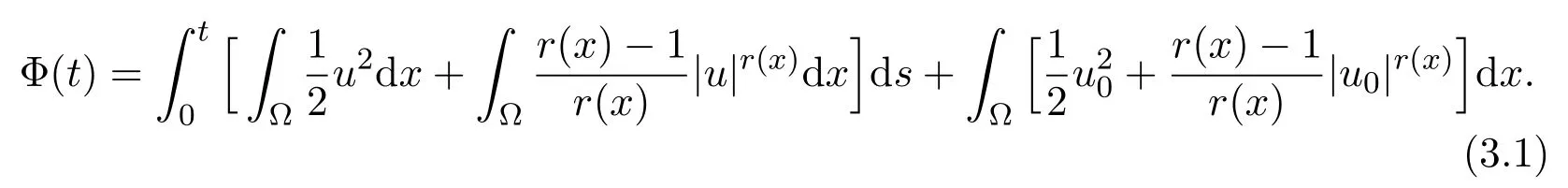
ProofWe multiply equation(1.1)by u and integrate overΩto obtain

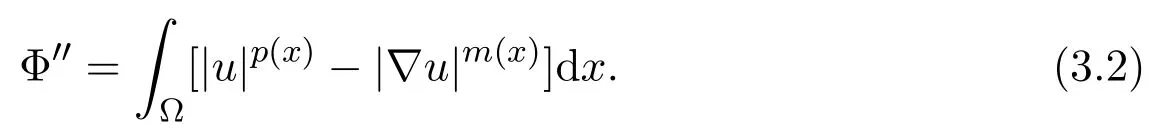
Similarly,we multiply equation(1.1)by utand integrate it overΩto get

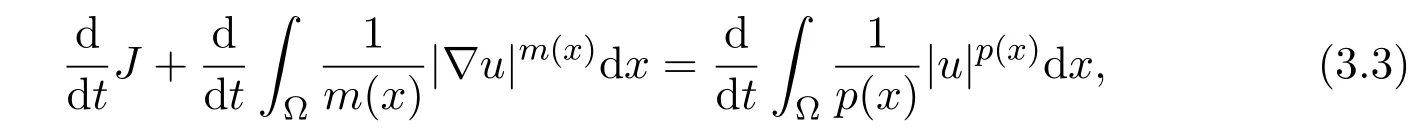
where

We observe that the following estimates hold

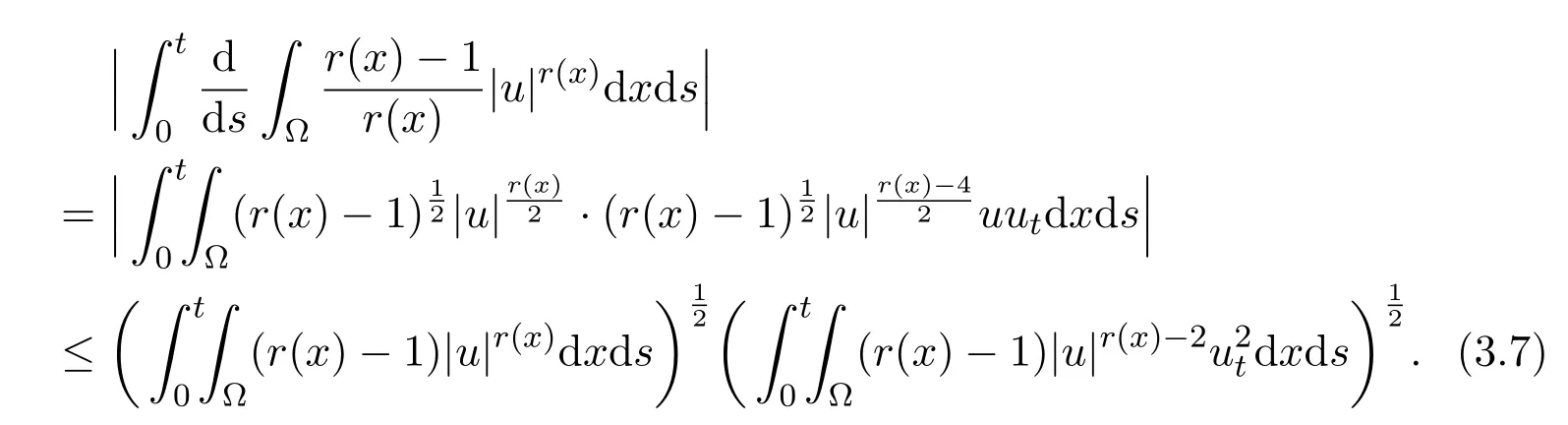
Thus,taking(3.6),(3.7)and the inequality(ab+cd)2≤(a2+c2)(b2+d2)into account,equality(3.5)yields

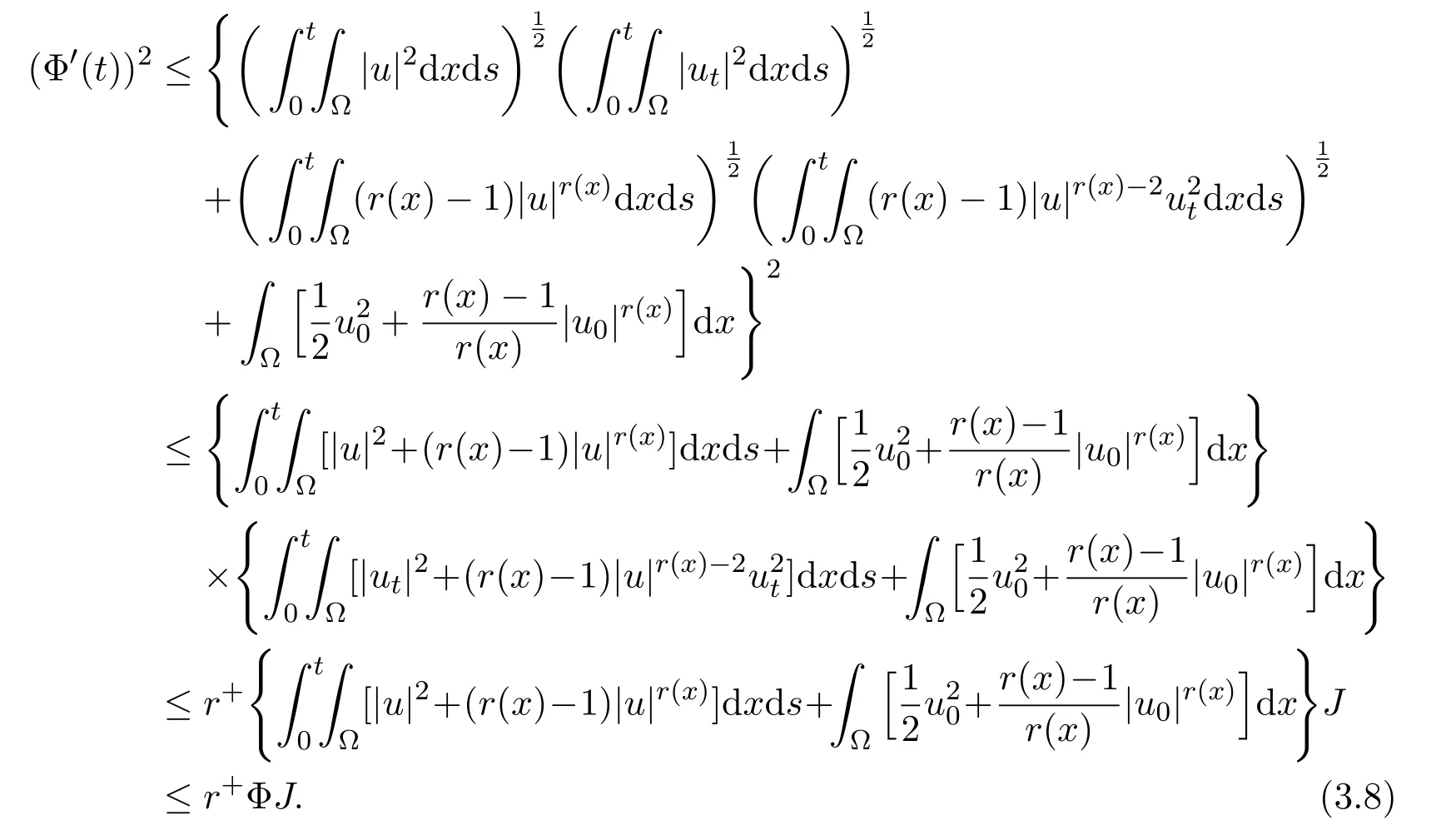
Now,integrating equality(3.3)with respect to time gives

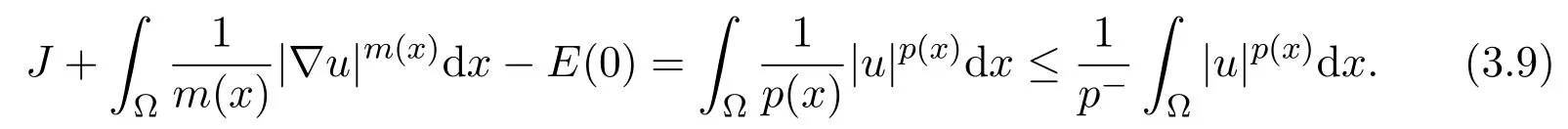
Combining(3.2)and(3.9)gives the inequality

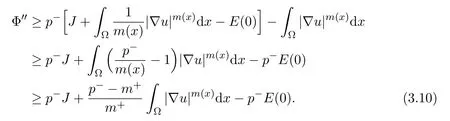
Noticing p−>m+,we conclude from(3.10)that

Multiplying(3.11)byΦ,from(3.8)and(3.11)we derive the differential inequality

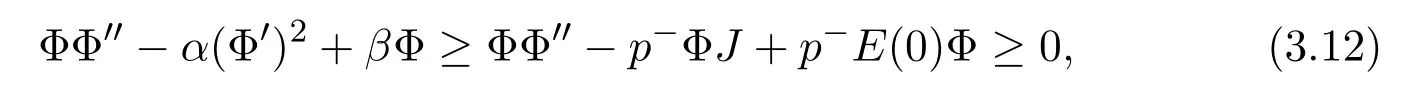
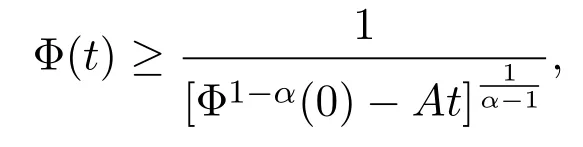
where

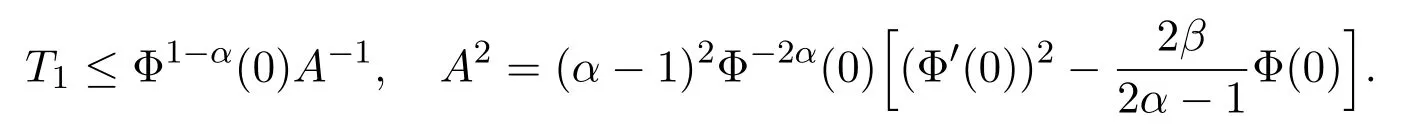
Thus,we have established the theorem.

AcknowledgementsThe authors would like to thank the referee for a careful reading of the manuscript,and for his or her valuable comments.