NOTE ON THE STABILITY PROPERTY OF THE VANISHING EQUILIBRIUM POINT OF AN ECOLOGICAL SYSTEM CONSISTING OF A PREDATOR AND STAGE STRUCTURE PREY∗†
2019-09-05XiaoyanHuangFengdeChen
Xiaoyan Huang,Fengde Chen
(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)
Abstract We revisit the stability property of an ecological system consisting of a predator and stage structure prey which was proposed by Raid Kamel Naji and Salam Jasim Majeed.By constructing some suitable Lyapunov function and applying the differential inequality theory,we show that the conditions which ensure the local stability of the vanishing point are enough to ensure its global stability.Our result supplements and complements some known results.
Keywords stage structure;predator-prey;global stability
1 Introduction
During the last decades,many scholars have investigated the dynamic behaviors of the ecosystem,see[1-18]and the references cited therein.Since many species have severalstates during their life,many scholars investigated the dynamic behaviors of the stage structured ecosystem,see references[1-16].Such topics as the extinction,persistent and stability have been extensively investigated.
Recently,Najiand Majeed [15]proposed the following ecological system consisting of a predator and stage structure prey
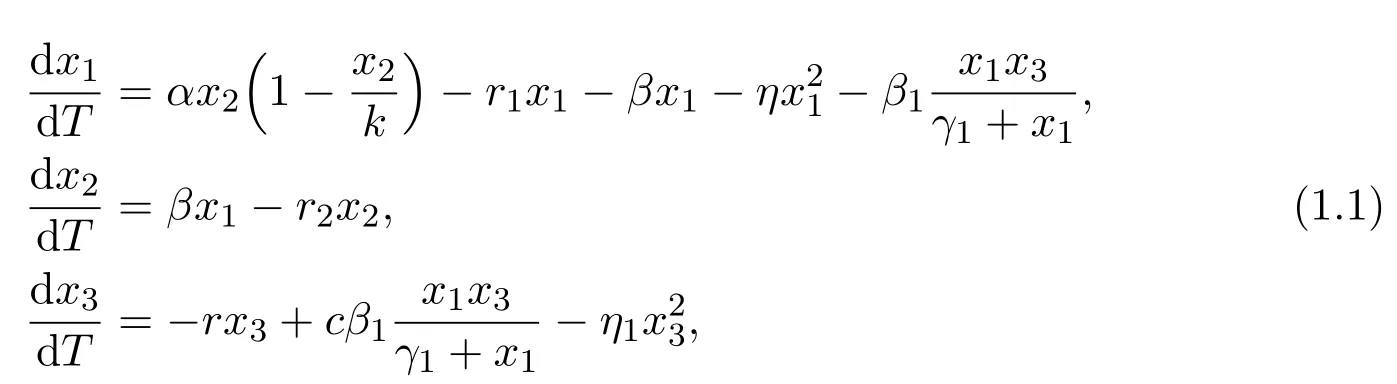
with the initial conditions x1(0)>0,x2(0)>0 and x3(0)>0.By introducing the following transformation
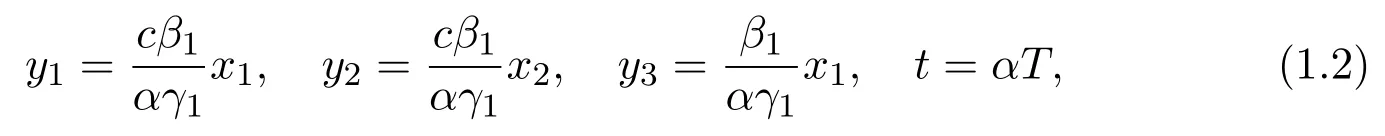
system(1.1)could be changed to
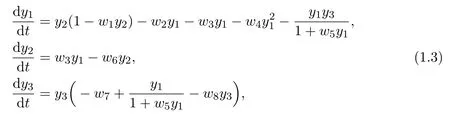
where wi,i=1,···,8,are all positive constants.System(1.3)always admits the vanishing equilibrium point E0(0,0,0),concerned with the stability property of this equilibrium,the authors obtained the following results.
Theorem AAssume that w3<(w2+w3)w6,then E0(0,0,0)is locally asymptotically stable.
Theorem BAssume that the vanishing equilibrium point E0(0,0,0)is locally asymptotically stable,then it is globally asymptotically stable in,provided that w6>1.
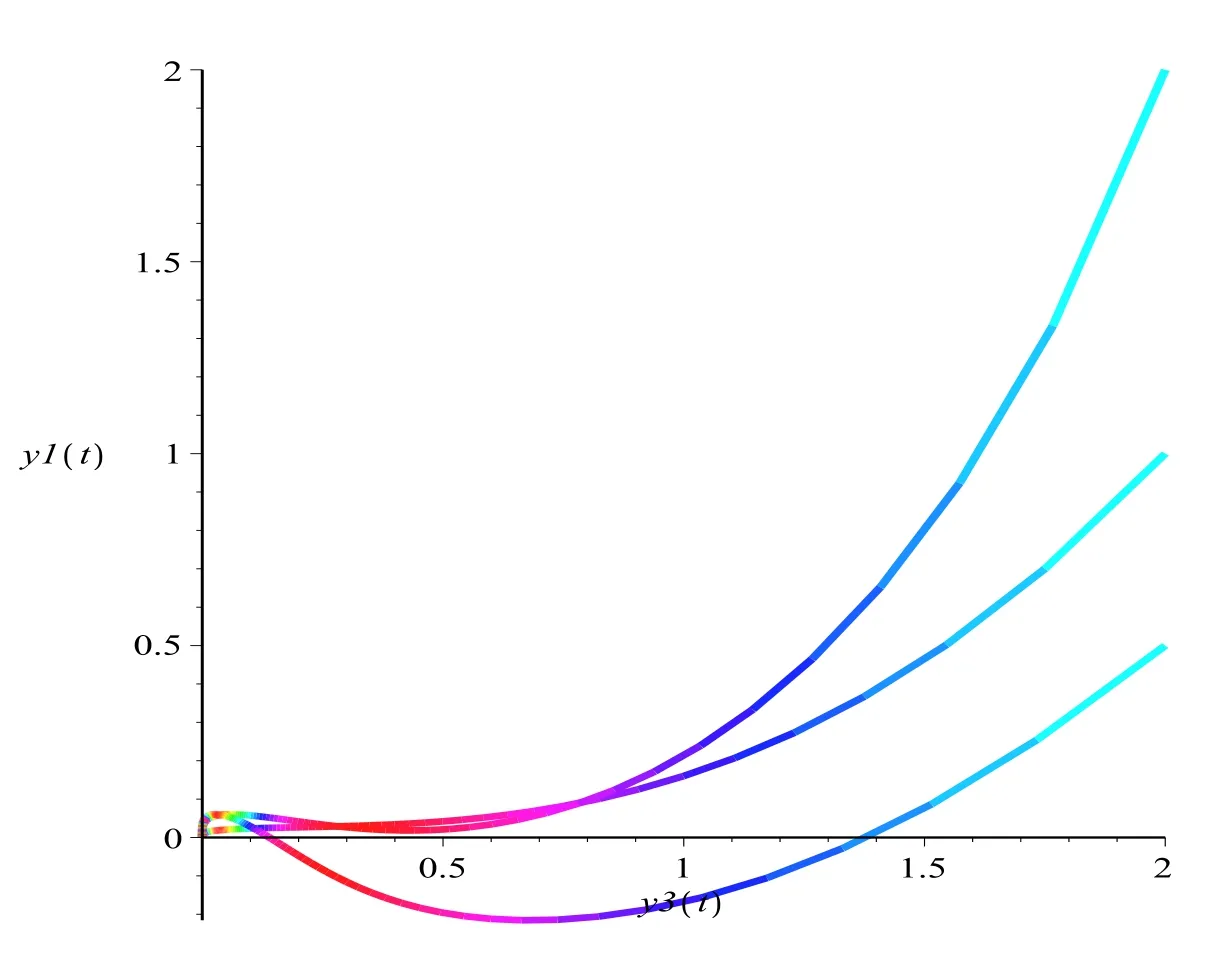
Now,an interesting issue is proposed:What would happen if 0 Let’s consider the following example. Example 1.1Consider the following system Here,we assume that w1=1,w2=3,w3=1,w4=w5=w7=w8=1,w6=.Then w6<1 and hold.That is,condition w6>1 in Theorem B could not hold,however,numeric simulation(Figure 1)shows that in this case,E0(0,0,0)is still globally asymptotically stable. Figure 1:Dynamics behaviors of system(1.4)with the initial conditions(y1(0),y2(0),y3(0))=(1,0,2),(2,1,2)and(0.5,2,2),respectively. Example 1.1 motivated us to propose the following conjecture. ConjectureThe conclusion of Theorem B still holds for the case 0 The aim of this paper is to give an affirm answer to the above conjecture,more precisely,we will show that the conditions which ensure the local asymptotic stability of the equilibrium E0(0,0,0)are enough to ensure its global asymptotic stability.Indeed,we have the following result. Theorem 1.1Assume that w3<(w2+w3)w6,then the vanishing equilibrium point E0(0,0,0)is globally asymptotically stable. Proof of Theorem 1.1From the first two equations of system(1.3),we have Now consider the following system (2.2)admits a boundary equilibrium E1(0,0).Now we show that under the assumption w3<(w2+w3)w6,the equilibrium E1(0,0)of system(2.2)is globally asymptotically stable.We will prove this by constructing some suitable Lyapunov function.Define a Lyapunov function One could easily see that the function V is zero at the boundary equilibrium E1(0,0)and is positive for all other positive values of u1and u2.The time derivative of V along the trajectories of(2.2)is It then follows from w3<(w2+w3)w6that D+V(t)<0 strictly for all u1,u2>0 except the boundary equilibrium E1(0,0),where D+V(t)=0.Thus,V(u1,u2)satisfies Lyapunov’s asymptotic stability theorem[18],and the boundary equilibrium E1(0,0)of system(2.2)is globally asymptotically stable.That is,letting(u1(t),u2(t))be any positive solution of system(2.2),one has Let(y1(t),y2(t),y3(t))be any positive solution of system(1.3)with initial condition(y1(0),y2(0),y3(0))=(y10,y20,y30),and(u1(t),u2(t))be the positive solution of system(2.2)with the initial condition(u1(0),u2(0))=(y10,y20),it then follows from the differential inequality theory that The positivity of the solution of system(1.3),(2.5)and(2.6)lead to Hence Forε>0 enough small,without loss of generality,we may assume thatε<,it then follows from(2.7)that there exists an enough large T>0 such that for all t>T, Hence,for t>T,from the third equation of system(1.3)and(2.8),we have Hence, (2.7)together with(2.9)ends the proof of Theorem 1.1. Najiand Majeed [15]proposed an ecological system consisting ofa predator and stage structure prey,that is system(1.1).By analyzing the eigenvalues of Jacobian matrix at E0(0,0,0),they showed that condition(1.5)is enough to ensure the local stability property of the above equilibrium.After that,by constructing some suitable Lyapunov function,they showed that the equilibrium E0is globally asymptotically stable if w6>1.In order to find out the dynamic behaviors of system(1.3)under the assumption 0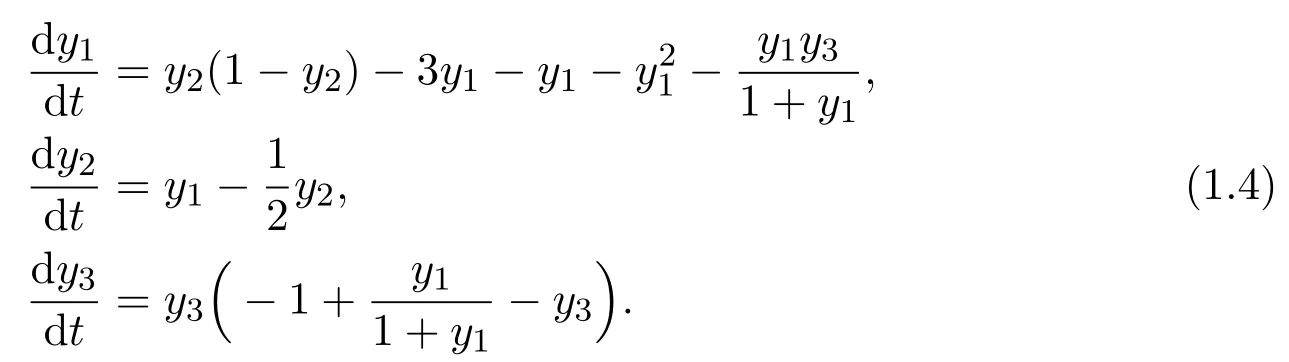

2 Proof of Theorem 1.1
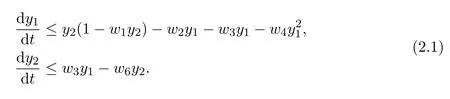
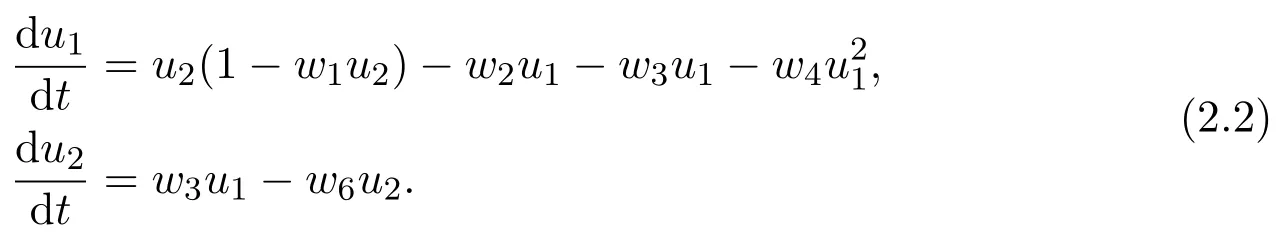
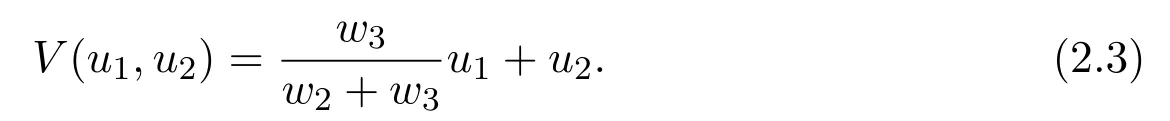
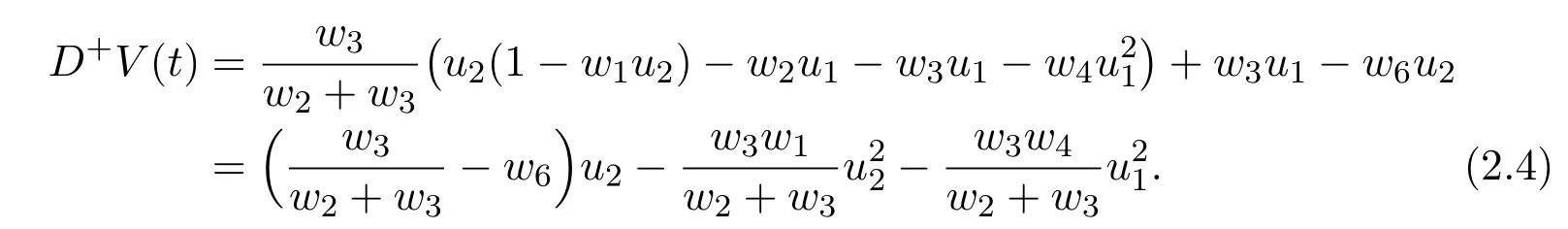
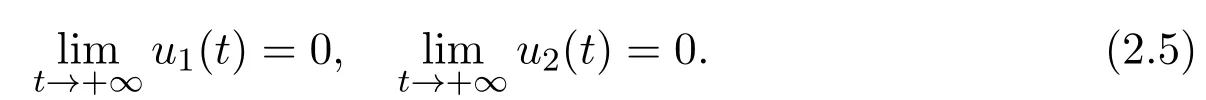
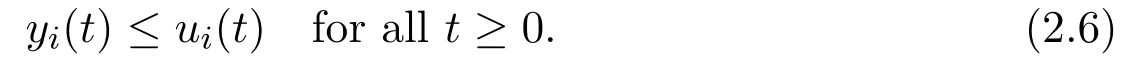
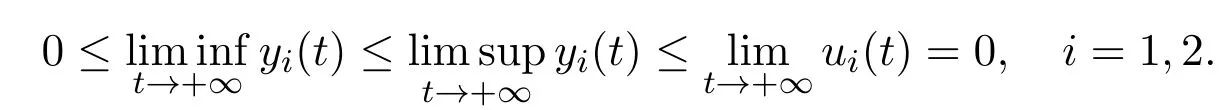


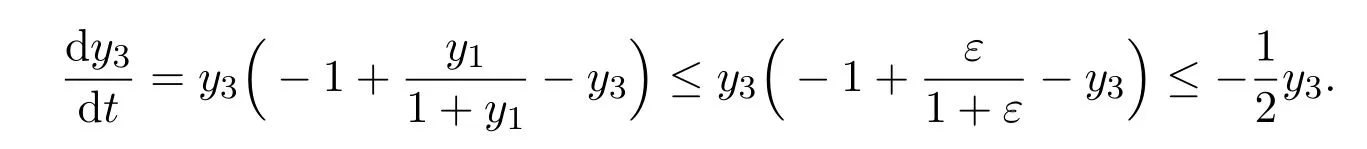

3 Discussion
杂志排行
Annals of Applied Mathematics的其它文章
- SOME PROBLEMS IN RADIATION TRANSPORT FLUID MECHANICS AND QUANTUM FLUID MECHANICS∗
- THE QUALITATIVE ANALYSIS OF A TWO SPECIES AMENSALISM MODEL WITH NON-MONOTONIC FUNCTIONAL RESPONSE AND ALLEE EFFECT ON SECOND SPECIES∗†
- A BLOW-UP RESULT FOR A CLASS DOUBLY NONLINEAR PARABOLIC EQUATIONS WITH VARIABLE-EXPONENT NONLINEARITIES∗†
- ASYMPTOTIC EIGENVALUE ESTIMATION FOR A CLASS OF STRUCTURED MATRICES∗†
- THE CAUCHY PROBLEMS FOR DISSIPATIVE HYPERBOLIC MEAN CURVATURE FLOW∗†
- GLOBAL EXISTENCE OF MILD SOLUTIONS FOR THE ELASTIC SYSTEM WITH STRUCTURAL DAMPING∗†
