SOME PROBLEMS IN RADIATION TRANSPORT FLUID MECHANICS AND QUANTUM FLUID MECHANICS∗
2019-09-05BolingGuo
Boling Guo
(Institute of Applied Physics and Computational Math.,Beijing 100088,PR China)
Jun Wu†
(The Graduate School of China Academy of Engineering Physics,Beijing 100088,PR China)
Abstract We introduce the radiation transport equations,the radiation fluid mechanics equations and the fluid mechanics equations with quantum effects.We obtain the unique global weak solution for the radiation transport fluid mechanics equations under certain initial and boundary values.In addition,we also obtain the periodic region problem of the compressible N-S equation with quantum effect has weak solutions under some conditions.
Keywords radiation transport equation;radiation fluid mechanics equations;fluid mechanics equations with quantum effects
1 Radiation Transport Equation and Radiation Fluid Mechanics Equations
A radiation transport equation is as follows

where I(υ,Ω)=I(x,t,υ,Ω)is the radiation intensity,S(υ)is the production rate of photons,σa(υ)is the absorption rate,σs(υ)is the scattering rate.In generally,σa=O(ραθ−β),α >0,β >0,where ρ is the density of matter,θ is the temperature of matter,and the radiation intensity of scattering out is

the radiation intensity of scattering in is
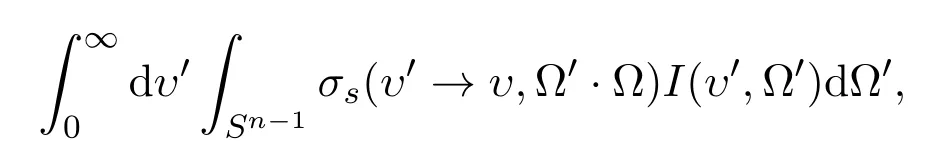
where Sn−1is the unit sphere in Rn−1.
Define the absorption coefficient and compton scattering nucleus
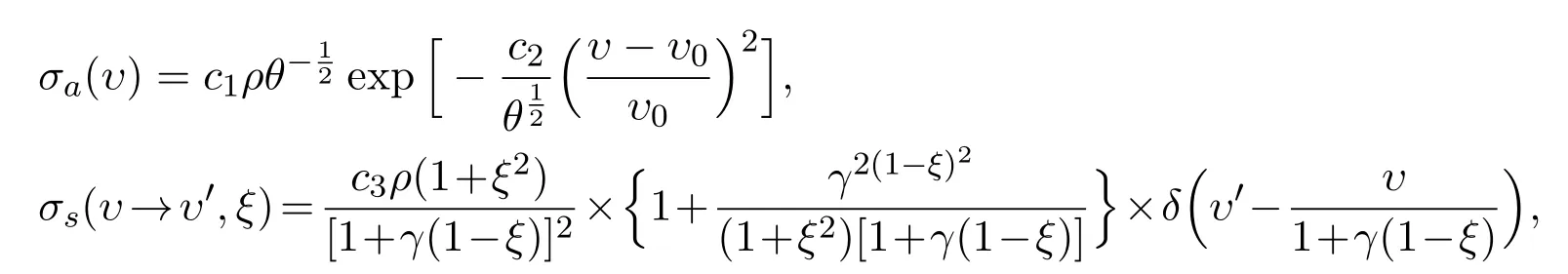
where γ =c4υ,ξ= Ω·Ω′,ci(i=1,···,4)are positive constants,υ0is the frequency.We now define the radiation energy density,radiation flux and radiation pressure as follows,respectively
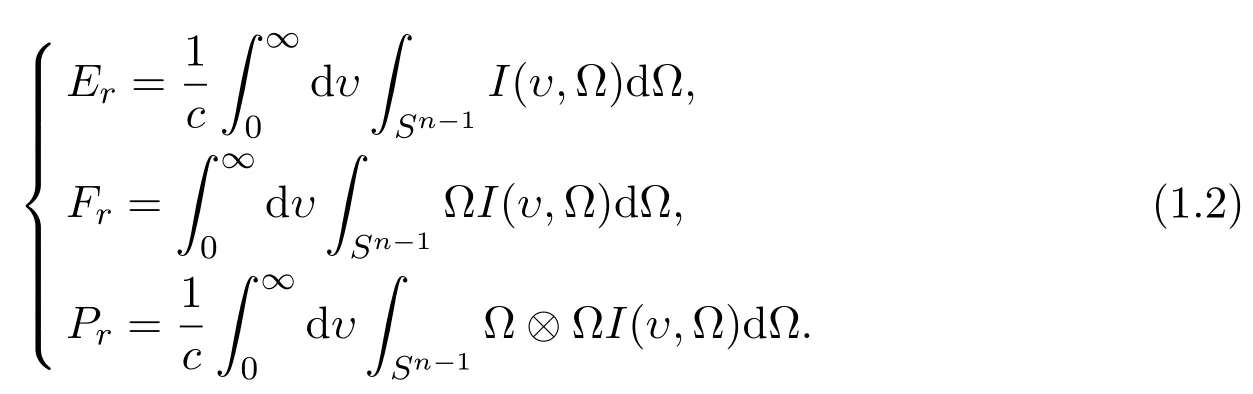
The radiation transport fluid mechanics equations are

where ρ,u,Pm=Pm(ρ,θ),Em=Em(ρ,θ)and θare the density,speed,pressure,internal energy and temperature of fluid,respectively.k=k(ρ,θ)is the thermal conductivity of fluid,S is the viscous tensor
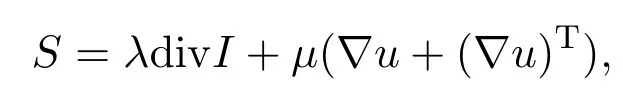
where λ and µ are viscous coefficients with 2λ+µ>0.
The radiant transport equation through the absorption of photons and after scattering interaction is
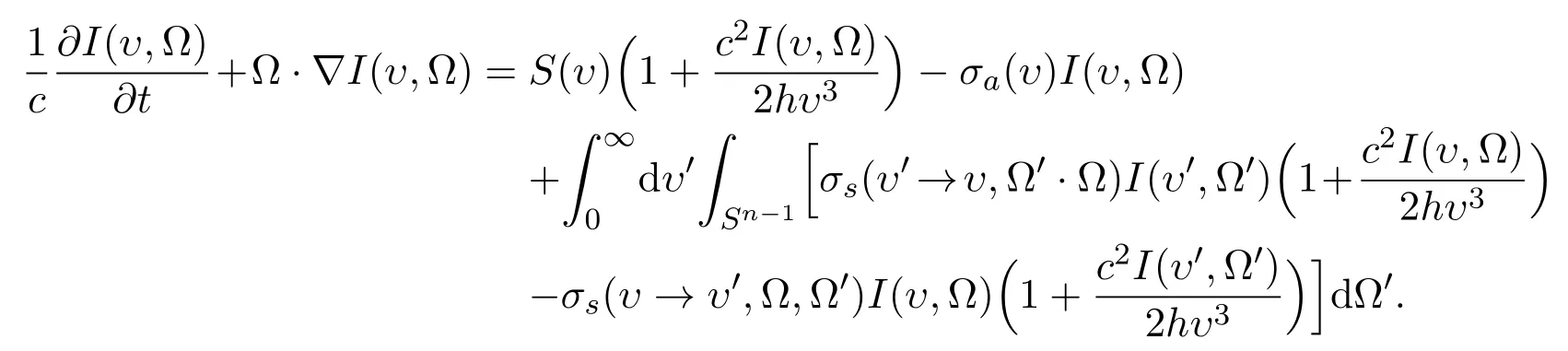
From S=σaB,σ=,then we can get

(1.3)with(1.4)form the system of radiation transport fluid mechanics by(1.2),where,h is the plank constant,B is the plank function,κis the Boltzmann constant.
Diffusion approximation
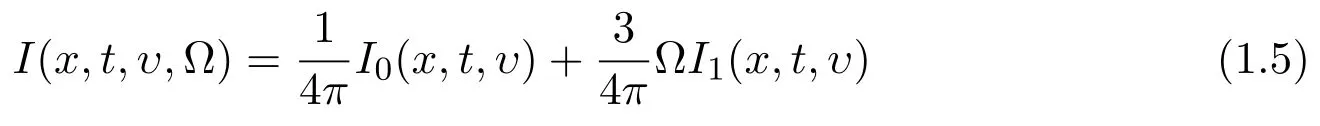
can be integrated as
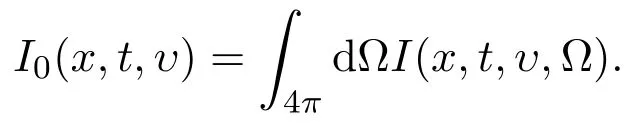
Multiply(1.5)by Ω and integrate it,then
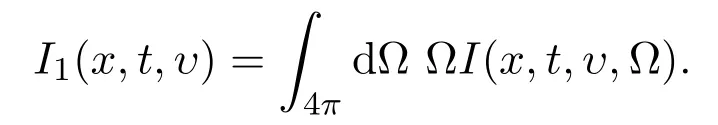
Put the expressions of(1.5)and I0,I1into(1.4),multiply it byΩto integrate,we can omit c−1∂tI1and assume the scattering kernel is diagonal,then we obtain

Put(1.5)into(1.4),which can be integrated with respect to Ω and with the Fick law,there is
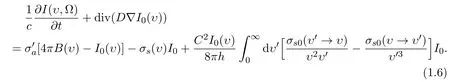
We call(1.6)as diffusion approximation of(1.4).
By balanced diffusion approximation,we can set I0(x,t,υ) ∼ I0(υ),then(1.6)can be represented by approximate radiation field
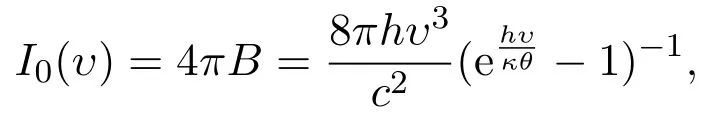
and obtain
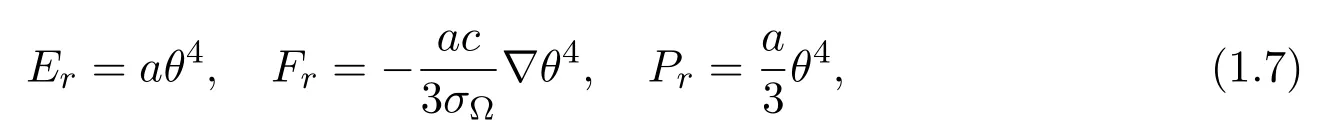
where σΩ∼ aθmρ−mis Rossel and average.
Consider the boundary condition
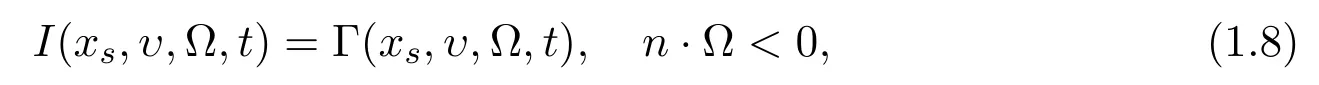
where we denote the known function of arguments,one point of surface and normal vector of this point as Γ,xs,n.For the vacuum conditions of free surfaces of(1.8),
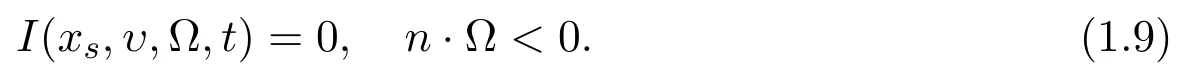
2 Some Related Results
(1)Consider the systems
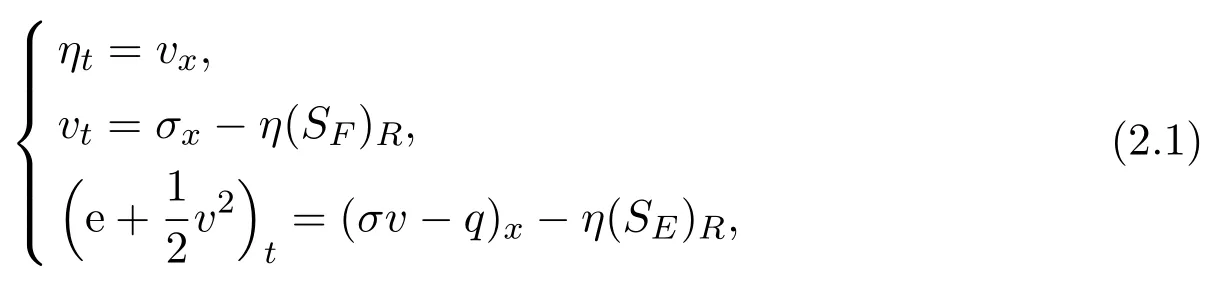
and the transport equation

with boundary conditions
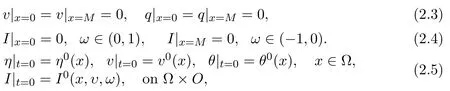
where
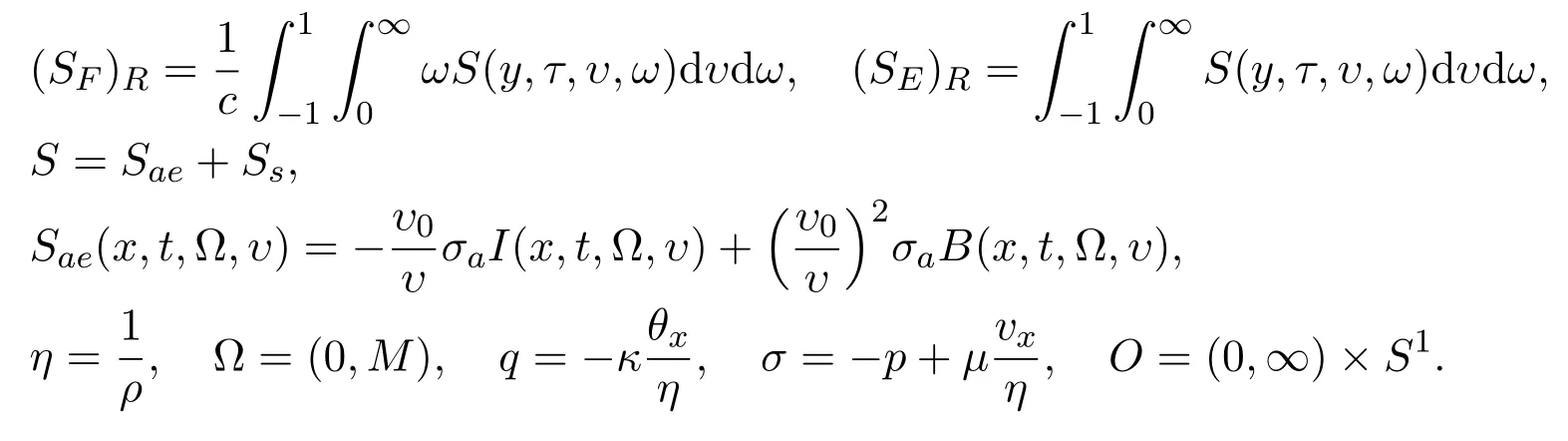
Theorem2.1Under the initial condition
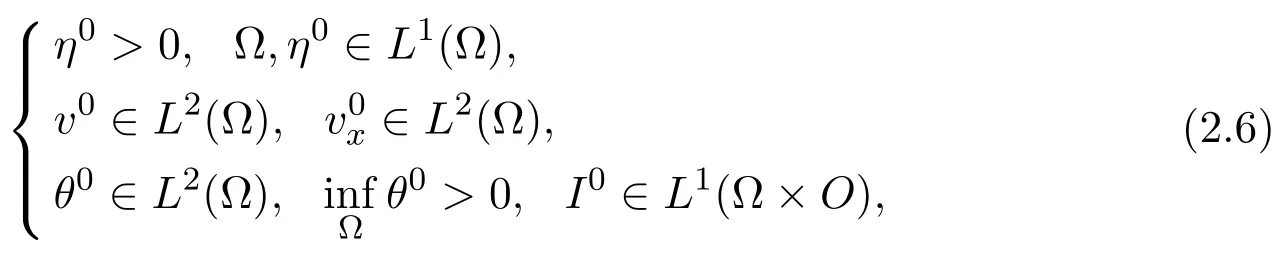
suppose that e,p,k satisfy some growth conditions,then there exists a unique global weak solution
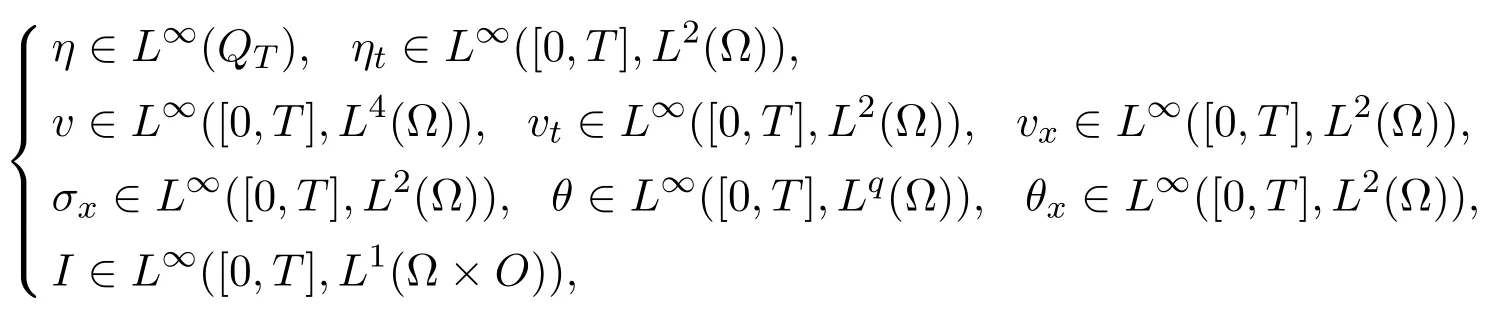
where QT=Ω×(0,T).
The weak solution is

x∈ Ω,t>0,and for any test function ϕ ∈ L2([0,T],H1(Ω)),ϕt∈ L1([0,T],L2(Ω)),ϕ(·,T)=0,which satisfy
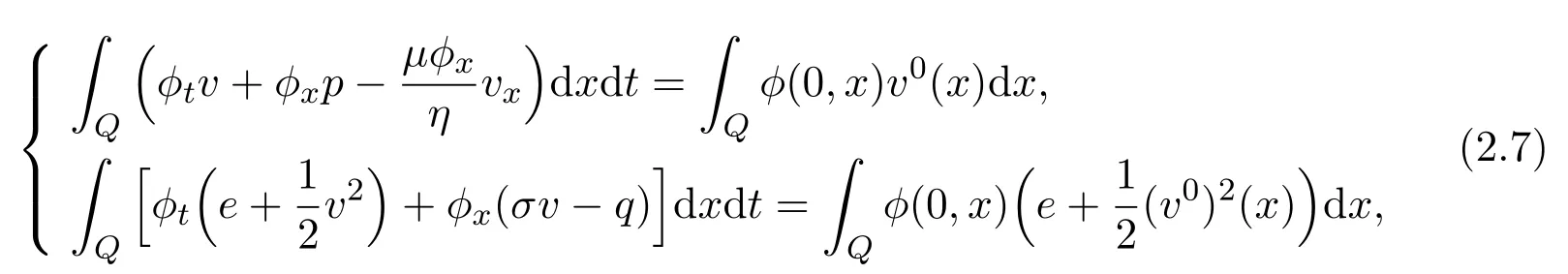
also for any test function ψ ∈ L2([0,T],H1(Ω ×O)),ψt∈ L1([0,T],L2(Ω ×O)),ϕ(·,T,·,·)=0,then we obtain
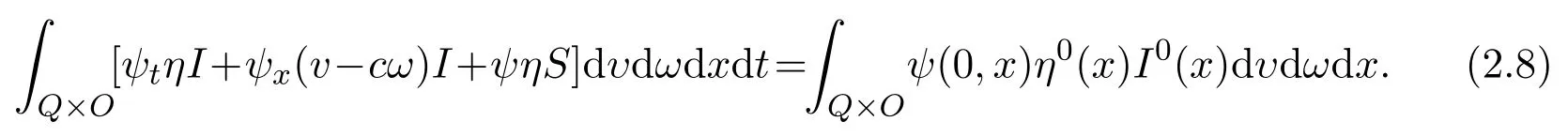
For the system

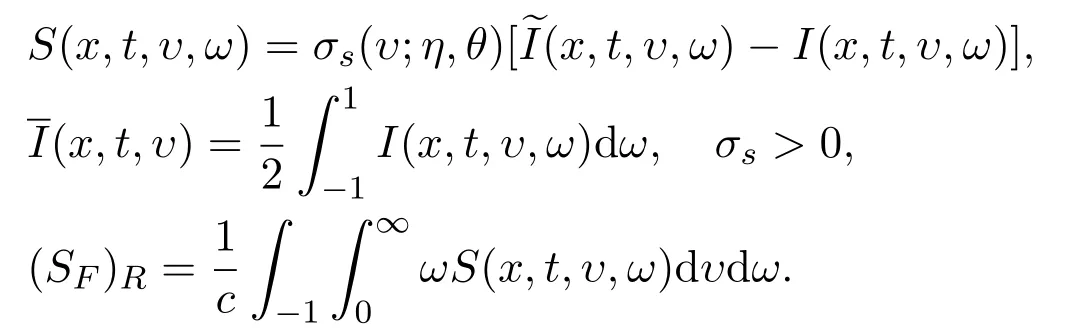
Theorem2.2Assume that the initialvalues of system(2.9)satisfy the condition as follows
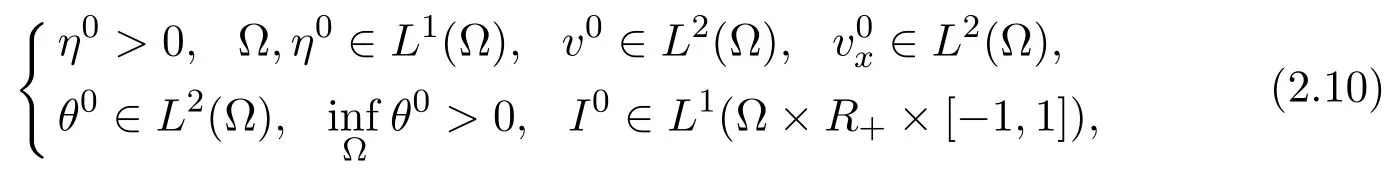
under the boundary value conditions
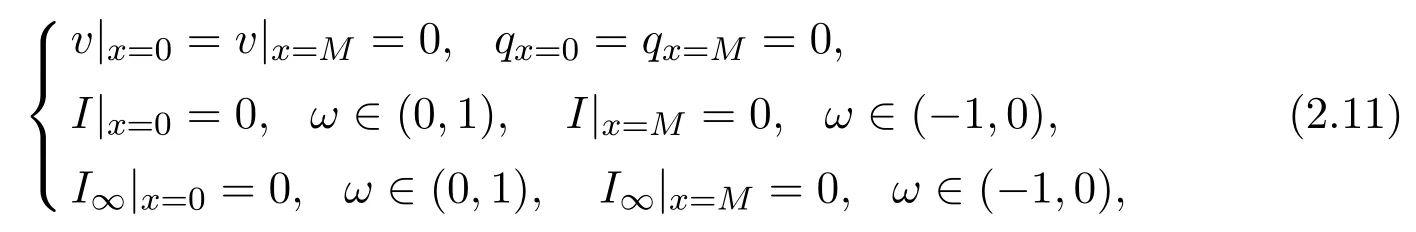
and the initial condition

then this system exists a unique global weak solution.
Theorem2.3Under the above conditions,the solution of equation(2.9)tends to a constant solution at t→ ∞ (η∞,v∞=0,θ∞,I∞=0).We can get the estimation
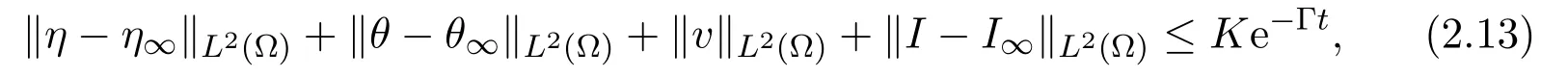
where Γ>0,t≥ t∞.
(2)We consider the following radiation transport fluid mechanic equation
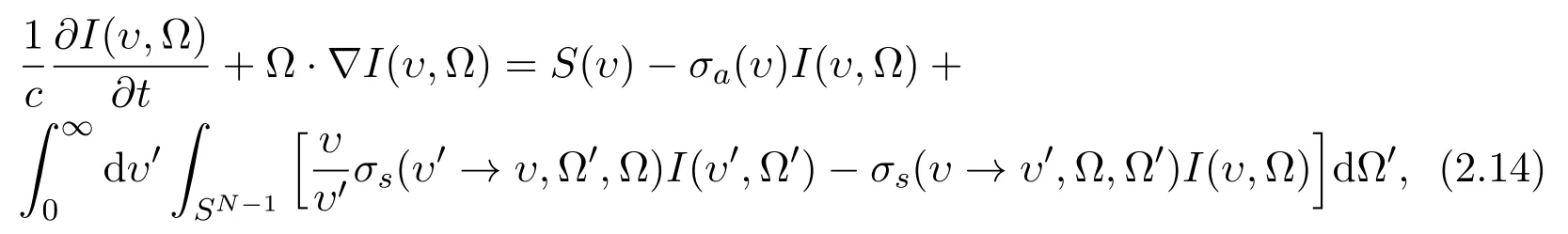
where I(υ,Ω)=I(x,t,υ,Ω),SN−1is the unit ball of SN,S(υ)=S(x,t,υ)is the energy production rate.Consider

with Em=cυρθ,Pm=Rρθ ≡ cυ(r − 1)ρθ.
We can rewrite(2.14),(2.15)as
where σ(υ)= σa(υ)+ σs(υ),with
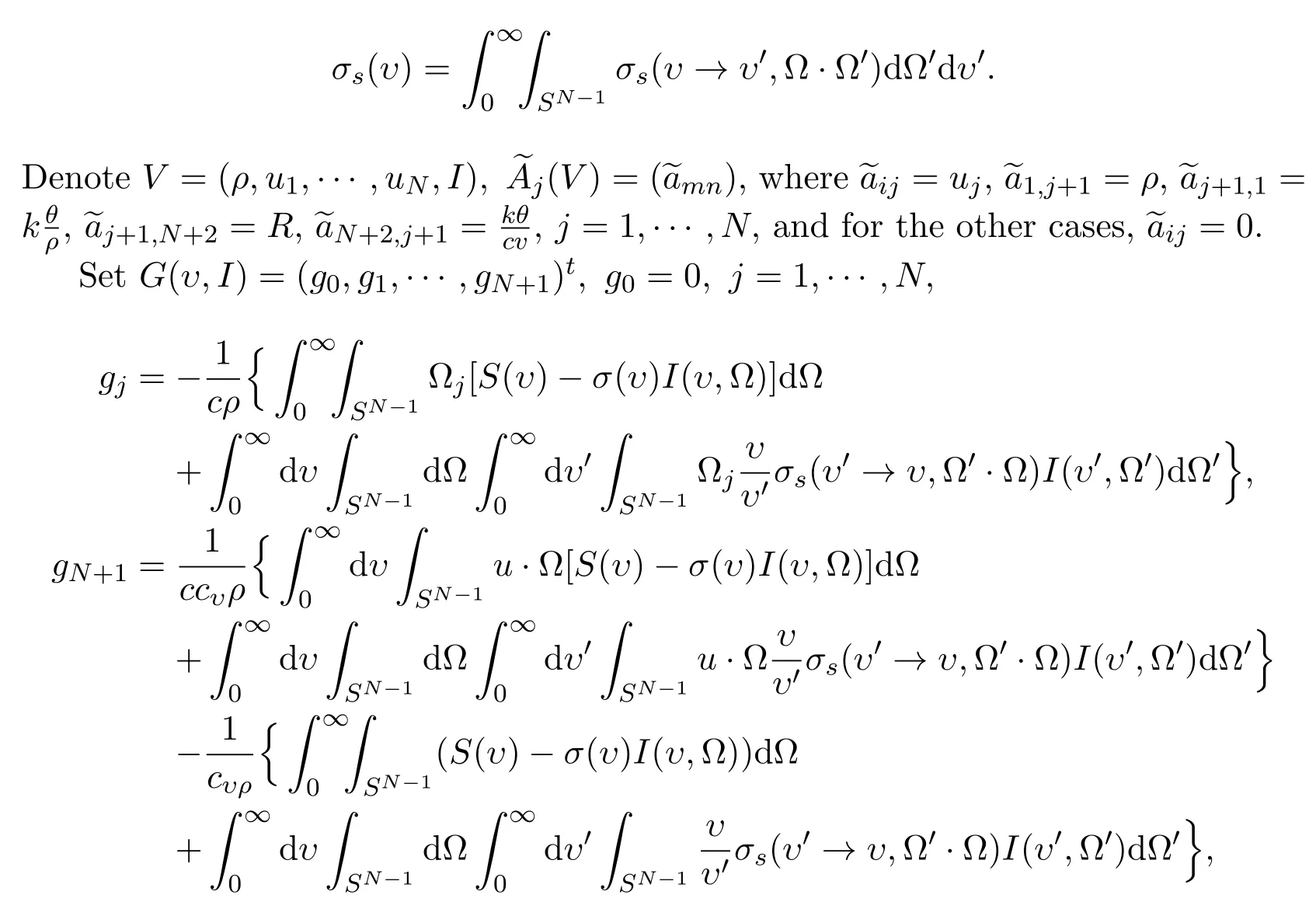
then we obtain
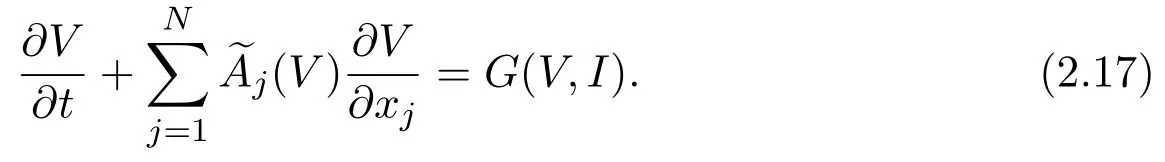
We now consider the cauchy initial value of(2.16),(2.17)
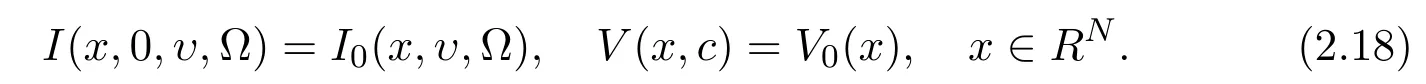
Theorem 2.4Assume that s>+1,and
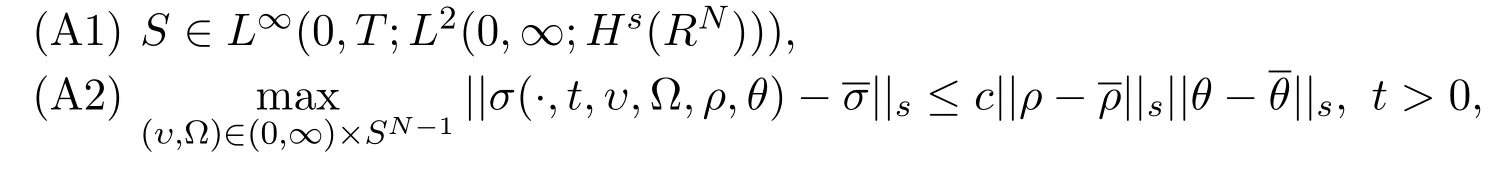


Remark(A1),(A2)can be satisfied,

where γ =c4υ, ξ= Ω ·Ω′,ci(i=1,···,4)are positive constants, υ0is a fixed frequency.Consider equations
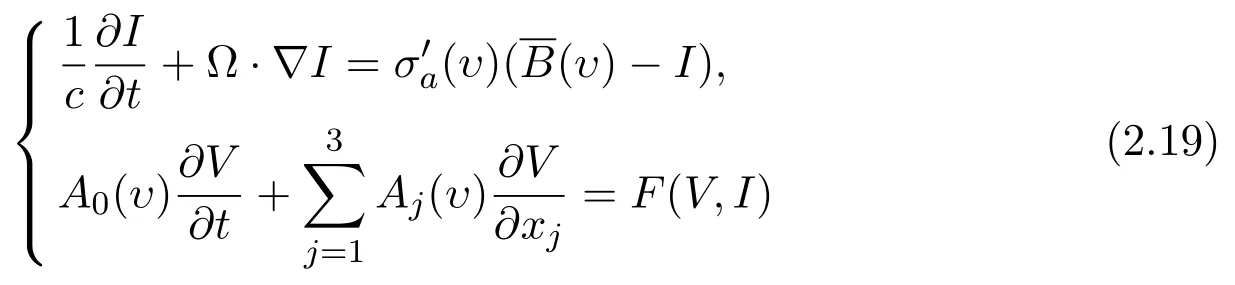
with the initial value
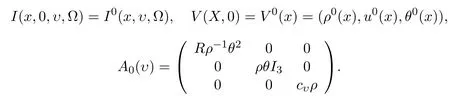
Symmetric matrix A(υ)=A0Bj(υ),Bj(υ)=(bmn)5×5,bij=uj,b1,j+1= ρ,bj+1,1=,bj+1,5=R,b5,j+1=,j=1,2,3,the others are zeros,

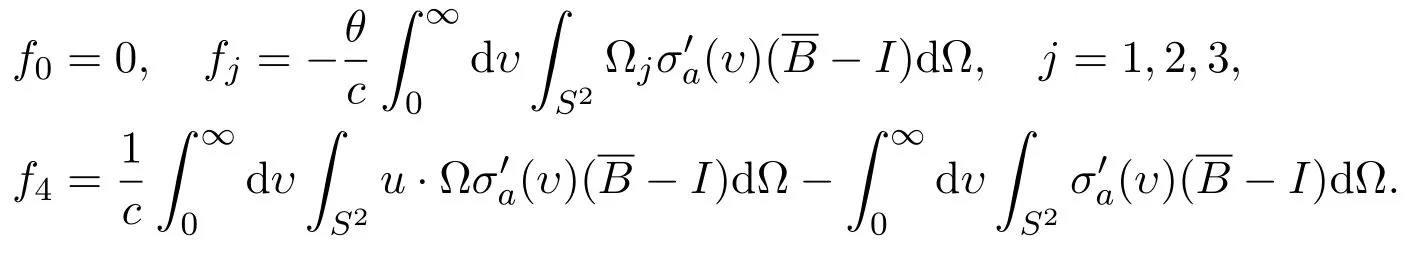
Set
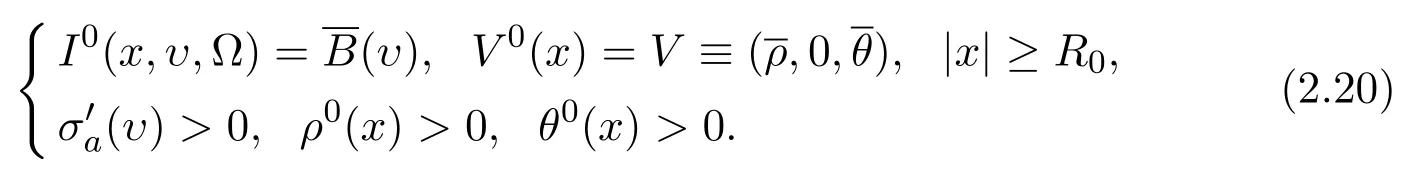
Denote

Theorem 2.5(finite speed of propagation)Suppose β≥1 and(2.20)holds.If the solution of(2.19)satisfies(V,I)∈C1,then(V,I)≡()∈E.
Theorem 2.6(blow up)Suppose(2.20)holds,and there exists a solution of(2.19)satisfying(ρ,u,θ,I) ∈ C1,0 ≤ t≤ T,where T is the maximum existence interval.If
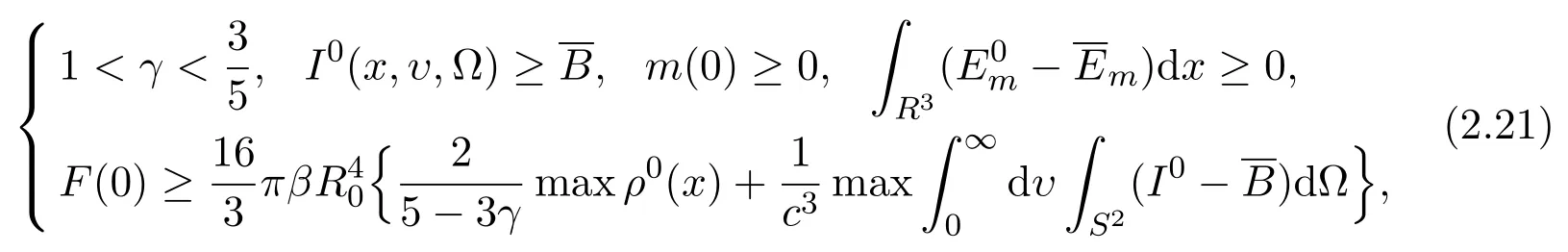
3 Plasma Two-fluid with Quantum Effect Equations
(1)Plasma two-fluid with quantum effect equations
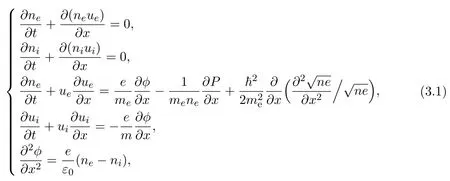
where ne,ni,uei,,ε0,P=P(ne)are electron number density,ion number density,electron ion fluid velocity,Planck constant,vacuum constant and electronic pressure,respectively.
(2)Quantum Kdv equation
Expand this equation according to equilibrium
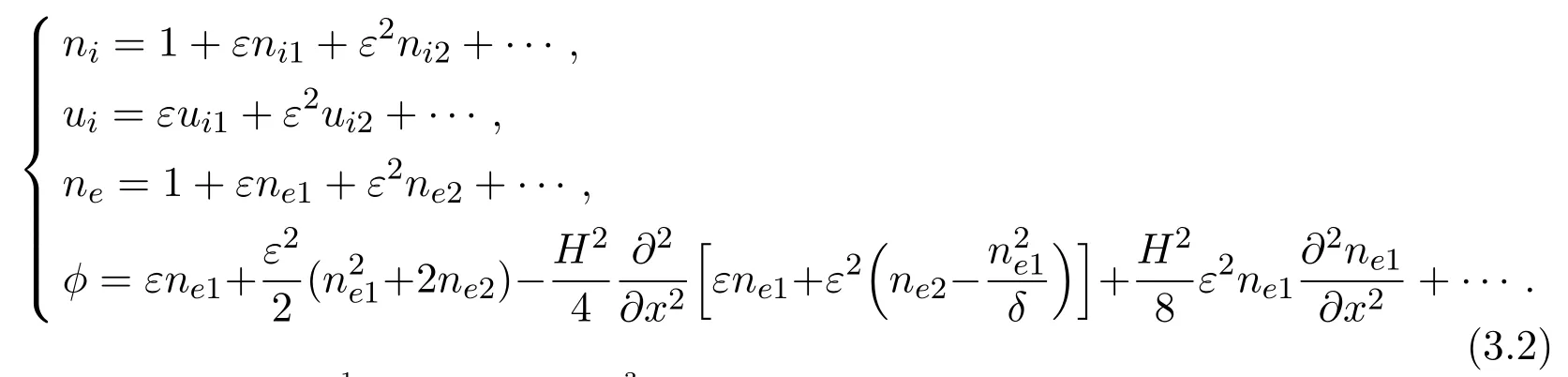

If H<2,
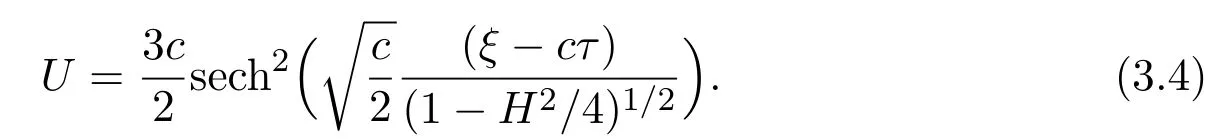
If H>2,
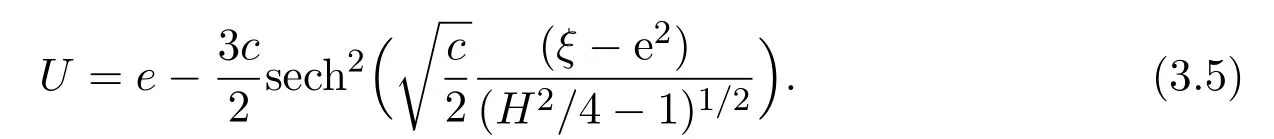
(3)Quantum electromagnetic fluid mechanics equations
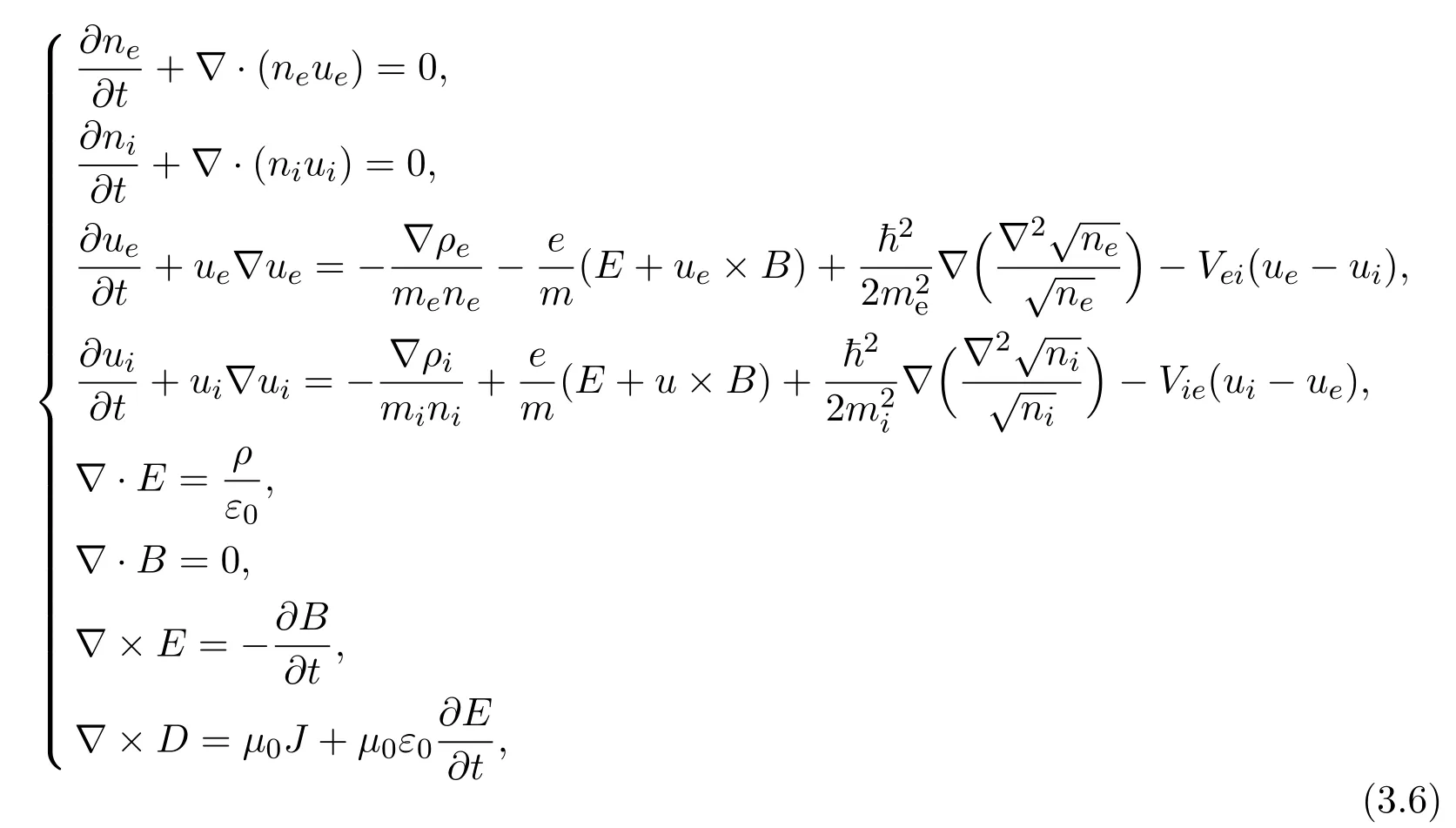
withρ=e(ni−ne),J=e(niui−neue).
Using
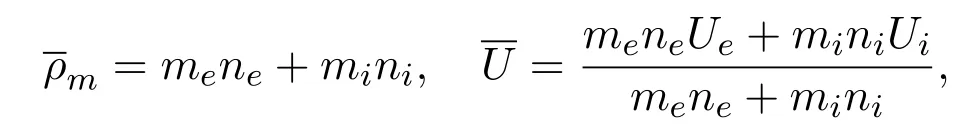
and the dimensionless quantity method,we can simplify the model as follows
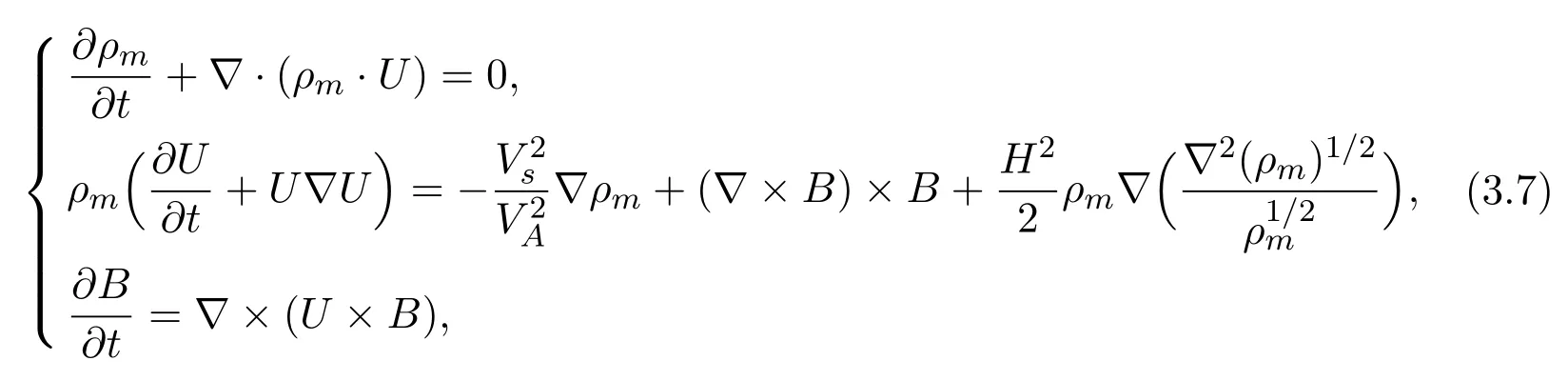
(4)One-dimensional and three-dimensional quantum Zakharov equations
One-dimensional quantum Zakharov equations are
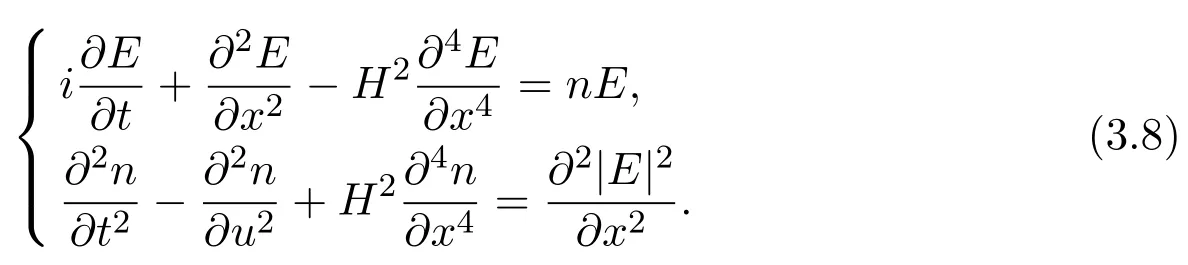
One-dimensional quantum nonlinear Schr¨o dinger equation is
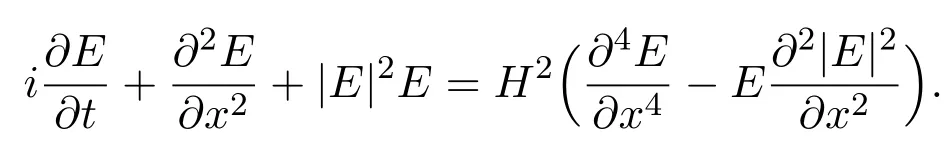
Three-dimensional quantum Zakharov equation is
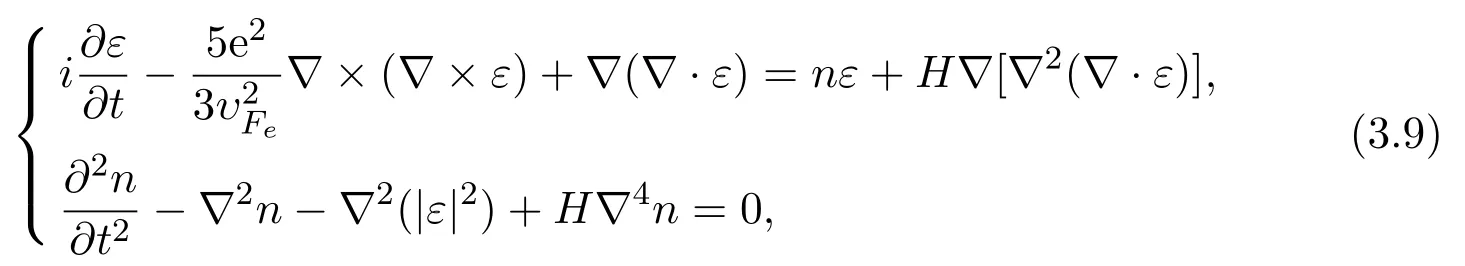
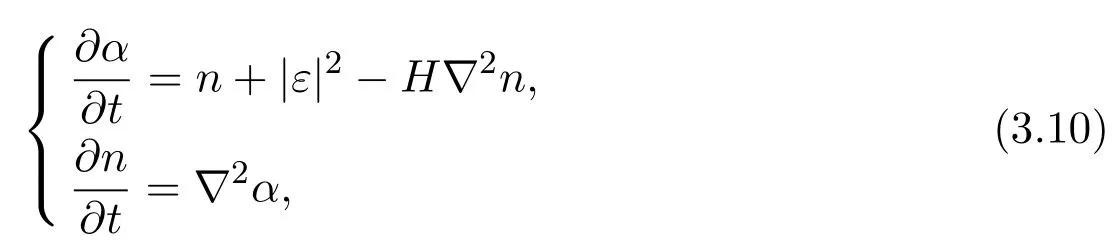
where
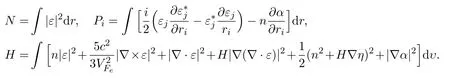
Consider two-dimensional and three-dimensional QVNLLS
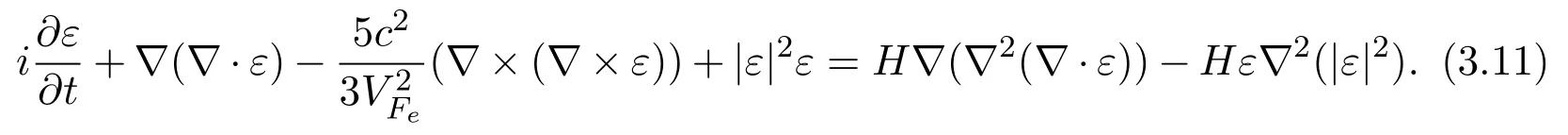
Two-dimensional variational solution is

Three-dimensional variational solution is
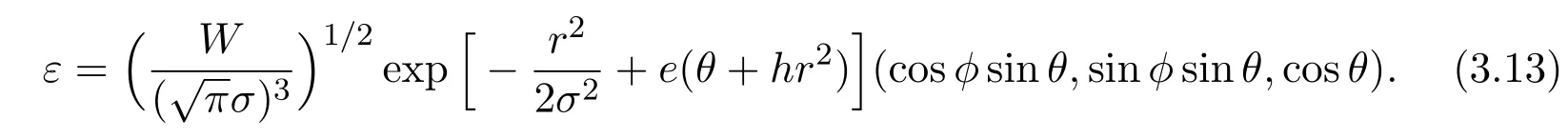
4 Some Results
(1)Consider the periodic region problem of the compressible N-S equation with the following quantum effects
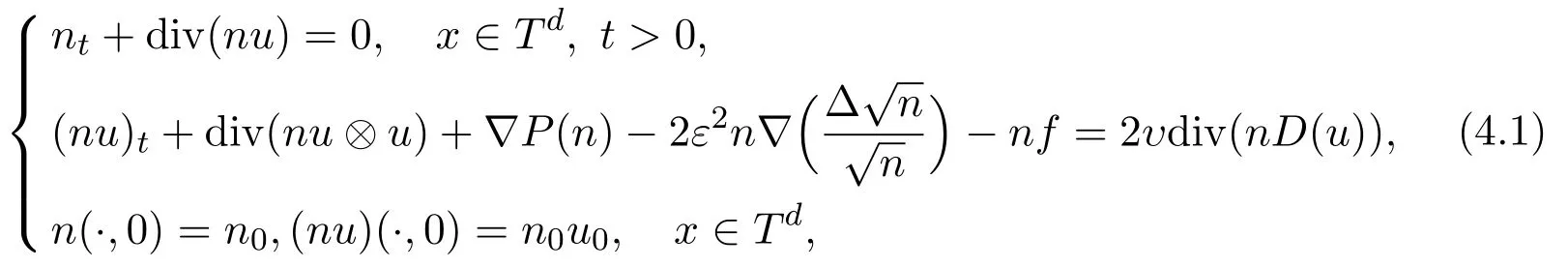
where u⊗u is the matrix of component uiuj,D(u)=(∇u+(∇u)T),d≤ 3,p(n)=nγ,γ≥1,υ>0.
From(4.1)1and(4.1)2,we obtain
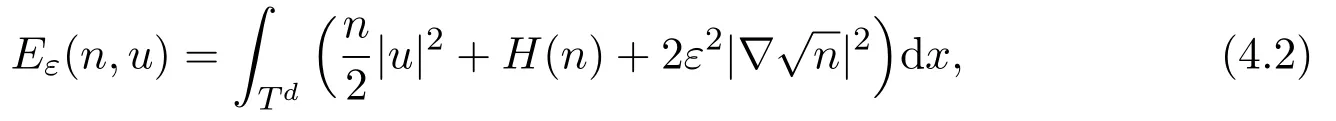
Formally for f=0,

In order to solve the compactness of,we introduce

then we can rewrite(4.1)as

where ω0=u0+υ∇log n0,= ε2− υ2.Ifε> υ,f=0,then
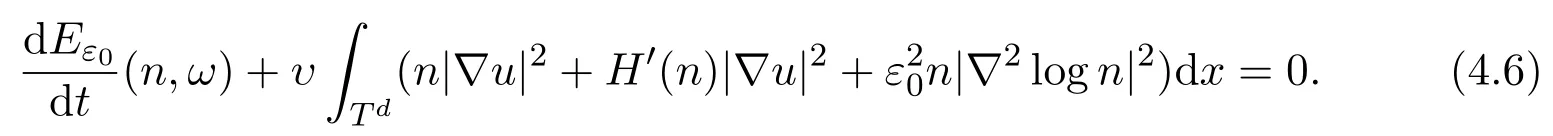
Theorem 4.1Assume that d≤ 3,T>0,ε0,υ >0,p(n)=nγ,γ >3(d=3),γ ≥ 1(d=2),f ∈ L∞(0,T;L∞(Td))such that n0≥ 0,Eε0(n0,ω0)is finite,then there exists a weak solution of(4.5)

which satisfies point for point in smooth experimental function ϕ of(4.5)with ϕ(·,t)=0 satisfying

Corollary 4.1Assume that d≤ 3,T>0,ε,υ>0,ε> υ,p(n)=nγ,γ>3(d=3),γ ≥ 1(d=2),f ∈ L∞(0,T;L∞(Td))such that n0>0,Eε(n0,u0+υ∇log n0)<∞,then according to Theorem 4.1 there exists a solution of(4.1)
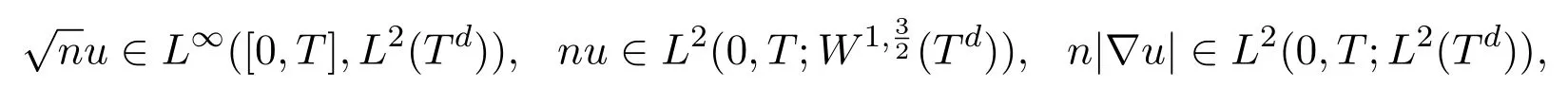
and for the experimental function ϕ,ϕ(·,t)=0 satisfies
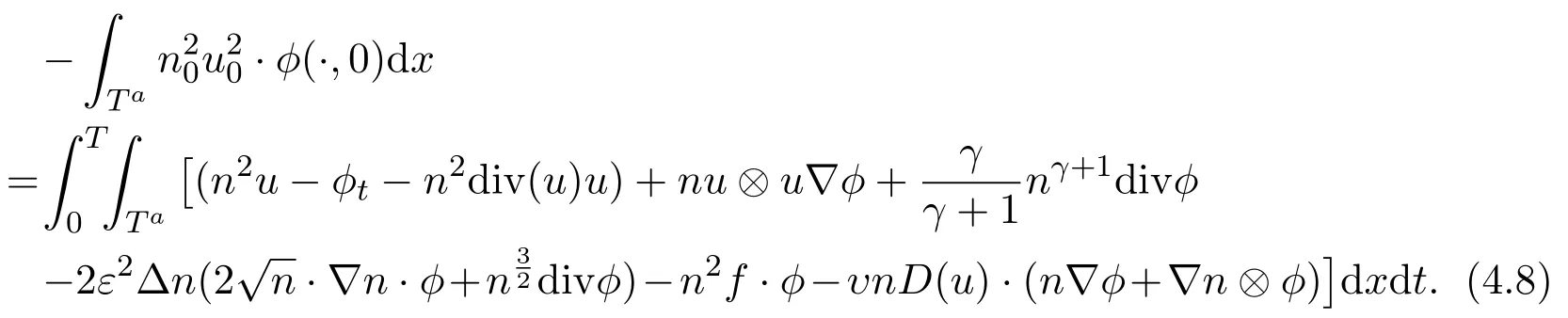
(2)Consider the periodic initial value problem of the N-S equation with the following quantum effects

where P(n)=nγ,n ≥ 1,µ(n)=αn,or µ(n)= α.
From(4.9)1and(4.9)2,we can get

where H(n)=nγ/(γ−1);H(n)=n(log n−1),γ=1.If∇V=0,then

We introduce w=u+α∇log log n,
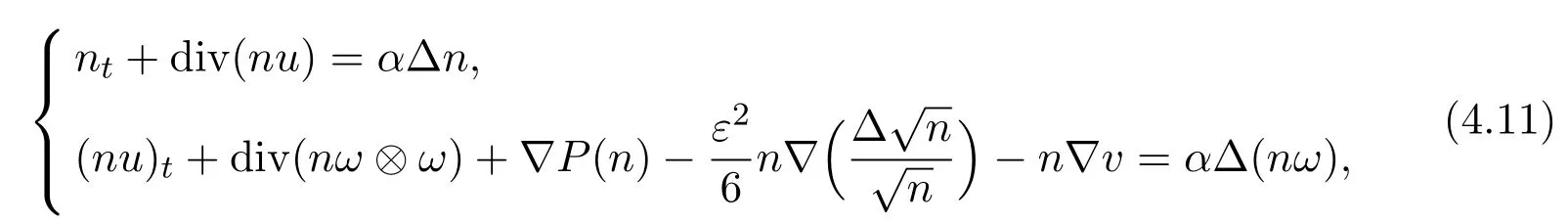
where ω0=u0+α∇log n0,ε0= ε2−12α2.Ifε2>12α2and ∇v=0,then

Using the inequality

Theorem 4.2Assume that d≤3,α>0,p(n)=nγ,γ>3(d=3),γ>1(d=2),∇V ∈C∞(0,∞;L∞(Td))such that m0≥0,Eq(n0,u0+α∇log n0)<∞,then there exists a weak solution of(4.5)and
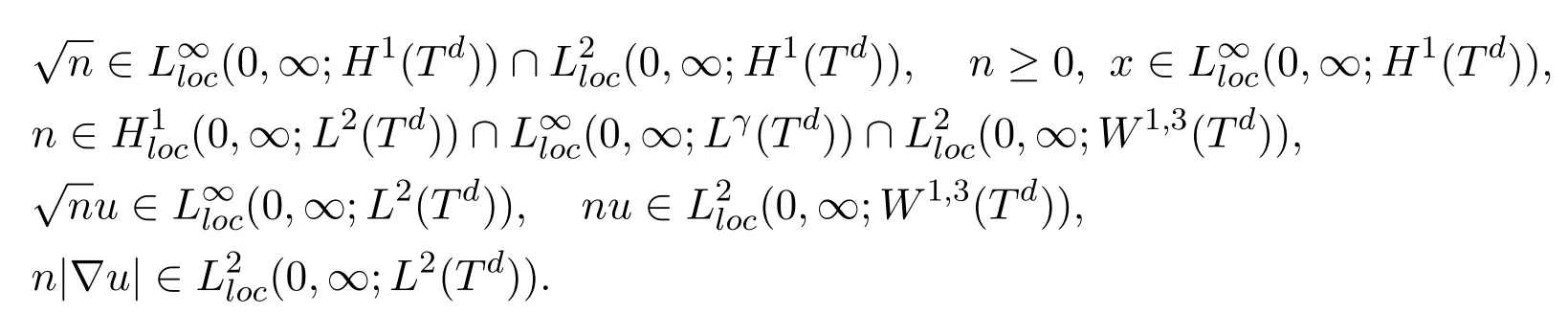
杂志排行
Annals of Applied Mathematics的其它文章
- THE QUALITATIVE ANALYSIS OF A TWO SPECIES AMENSALISM MODEL WITH NON-MONOTONIC FUNCTIONAL RESPONSE AND ALLEE EFFECT ON SECOND SPECIES∗†
- NOTE ON THE STABILITY PROPERTY OF THE VANISHING EQUILIBRIUM POINT OF AN ECOLOGICAL SYSTEM CONSISTING OF A PREDATOR AND STAGE STRUCTURE PREY∗†
- A BLOW-UP RESULT FOR A CLASS DOUBLY NONLINEAR PARABOLIC EQUATIONS WITH VARIABLE-EXPONENT NONLINEARITIES∗†
- ASYMPTOTIC EIGENVALUE ESTIMATION FOR A CLASS OF STRUCTURED MATRICES∗†
- THE CAUCHY PROBLEMS FOR DISSIPATIVE HYPERBOLIC MEAN CURVATURE FLOW∗†
- GLOBAL EXISTENCE OF MILD SOLUTIONS FOR THE ELASTIC SYSTEM WITH STRUCTURAL DAMPING∗†
