ASYMPTOTIC EIGENVALUE ESTIMATION FOR A CLASS OF STRUCTURED MATRICES∗†

Juan Liang

(School of Math.and Statistics,Minnan Normal University,Zhangzhou 363000,Fujian,PR China)

Jiangzhou Lai‡

(School of Math.and Computer Science,Fuzhou University,Fuzhou 350108,Fujian,PR China)

Qiang Niu

(Dept.of Mathematical Sciences,Xi’an Jiaotong-Liverpool University,Suzhou 215123,Jiangsu,PR China)

Abstract In this paper we consider eigenvalue asymptotic estimations for a class of structured matrices arising from statistical applications.The asymptotic upper bounds of the largest eigenvalue(λmax)and the sum of squares of eigenvaluesare derived.Both these bounds are useful in examining the stability of certain Markov process.Numerical examples are provided to illustrate tightness of the bounds.

Keywords Toeplitz matrix;eigenvalue;rank-one modification;trace

1 Introduction

The necessity of analyzing asymptotic behavior of eigenvalue distribution of structure matrices,e.g.,Toeplitz matrices,block Toeplitz matrices and Toeplitz like matrices,arise in many fields of applications[1-3].The eigenvalue distribution of sequences of symmetric Toeplitz matrices was revealed[1].As an application,these results have been applied to the study of covariance matrices of a second order stationary process.In more recent research,extensions have been made to block Toeplitz matrices with non-Toeplitz blocks[4,5].In this paper,we consider a class of structure matrices arising in the study of order statistics under exponentiality.The matrix A ∈ Rn×nis structured with its entries be defined by

where P is a parameter with an order normally less than,n→+∞.

Let λi,i=1,2,···,n,be eigenvalues of A,and λmaxbe the largest eigenvalue.Then λmaxis the optimal constant of certain logarithmic Sobolev inequality,andis a useful quantity in related applications.Therefore,upper bounds of λmaxandare important in determining asymptotic stability of the process.In this note,we intend to give proper upper bounds for λmaxandrespectively,as n→∞.

By the definition of matrix A,it is easy to see that A is a positive matrix[6].For simplicity,we denote positive matrix A by A>0 and the nonnegative matrix A by A≥0.The following results are useful in deriving the main results of the paper.For completeness,we list them as follows.

Lemma 1[7]Let B≥0 be an irreducible matrix.Then:

(1)The matrix B has a positive real eigenvalue equal to its spectral radius;

(2)the spectral radius ρ(B)is a simple eigenvalue of B;

(3)there is an eigenvector x>0 that is corresponding to eigenvalue ρ(B);

(4)ρ(B)increases when any entry of B increases.

Lemma 2[8]The positive matrix is irreducible.

This paper is organized as follows.In Section 2,by regarding matrix A as a rank-one modification of Toeplitz matrix,we derive the asymptotic upper bound for the largest eigenvalue.In Section 3,by computing the trace of A2,we obtain the asymptotic upper bound for the sum of squares of eigenvalues.Finally,we conclude the paper in Section 4.

2 Asymptotic Upper Bound of the Largest Eigenvalue

Then

Subsequently,let us recall the eigenvalue property of a rank-one modification of diagonal matrix.

Lemma 3[12]Suppose D=diag(d1,···,dn)∈ Rn×nand that diagonal entries satisfy d1>d2> ···>dn.Assume that ρ0 and that z ∈ Rnhas no zero components.If

then zTv0 and D − λI is nonsingular.

Based on Lemma 3,the following theorem has been established in[6,11].

Theorem 1[11]Let C=D+ρzzTwith D=diag(d1,···,dn)∈ Rn×nand||z||=1.Suppose d1≤d2≤···≤dn,and λ1≤λ2≤···≤λnto be the eigenvalues of C.Then

Moreover,

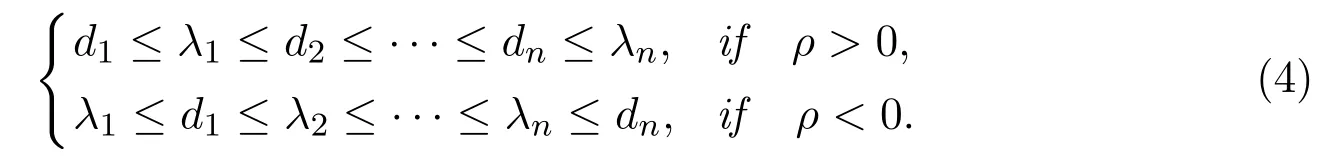
Finally,if diare distinct and all the elements of z are nonzero,then the eigenvalues of C strictly separate those of D.

Subsequently,we will estimate the largest eigenvalue of e A.As e A>0,from Lemmas 1 and 2 we know thatis irreducible and ρ()is a simple eigenvalue of.Then on the basis of Lemma 2.8[7],we have the following conclusion.

Lemma 4For positive matrix e A,then either

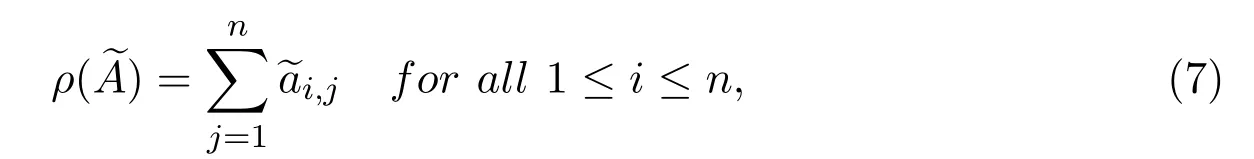
or

Based on Theorem 1 and Lemma 4,the largest eigenvalue of A can be bounded as follows.

Theorem 2The largest eigenvalue of A is bounded as follows

ProofAs ρ()is an eigenvalue of,from Theorem 1 we have

Moreover,from Lemma 4 we know that λmax(A)is bounded by.By the definition of,the maximum row sum occurs as follows

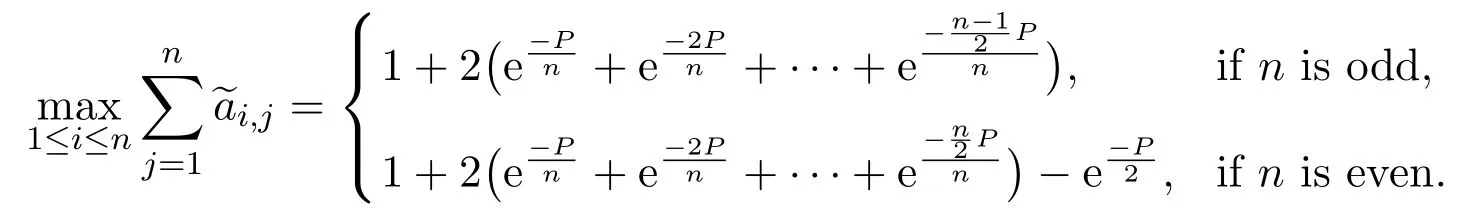
By simple arithmetic,we have

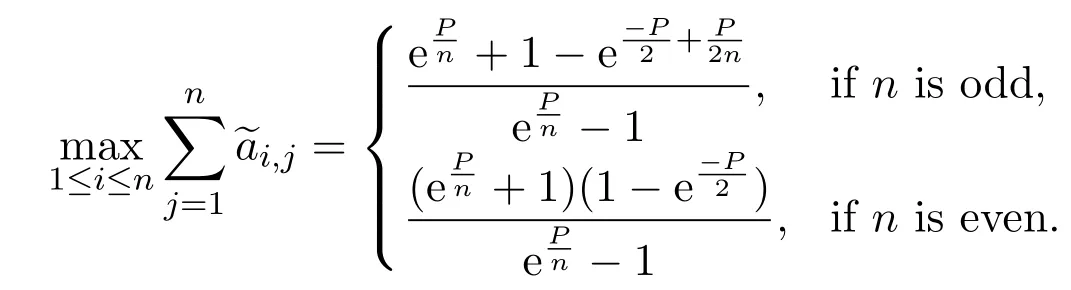
Thus,(9)holds.The proof is completed.

In practical applications,the parameter P is asymptotically less than.For P equals to,the largest eigenvalue and the upper bound derived in Theorem 1 is compared in Figure 1.The largest eigenvalue is computed by the power method[12].The algorithm is terminated once||Aφ−λmaxφ||≤ 10−3.From the figure we can see that the bound derived in Theorem 1 can bound the largest eigenvalue very well.

3 Asymptotic Upper Bound of

For matrix A,we also want to estimate the upper bound of.To deal with this problem,we convert the problem into the computing the trace of A2.

Let Aφi= λiφi,then

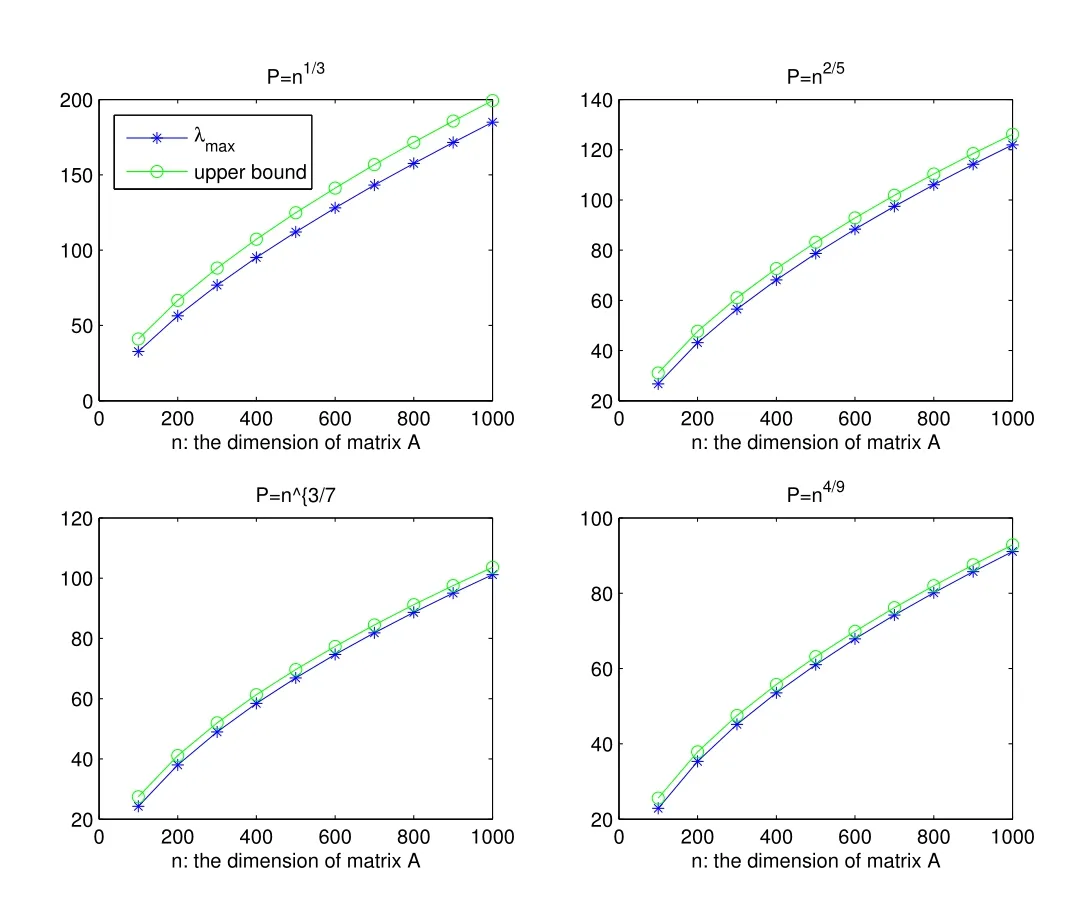
Figure 1:The largest eigenvalue vs the upper bound.

that is,λ2iis an eigenvalue of A2.So the sumequals to the trace of A2,where

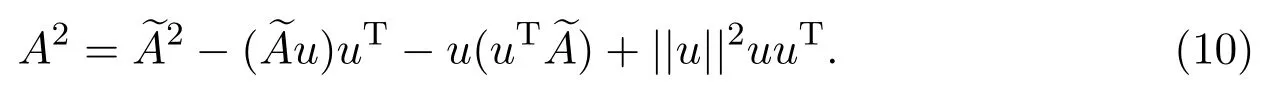
Therefore,

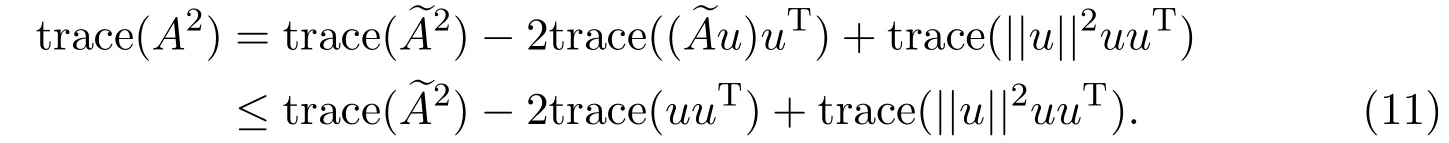
Subsequently,we estimate the right hand sides of(11).

Firstly,

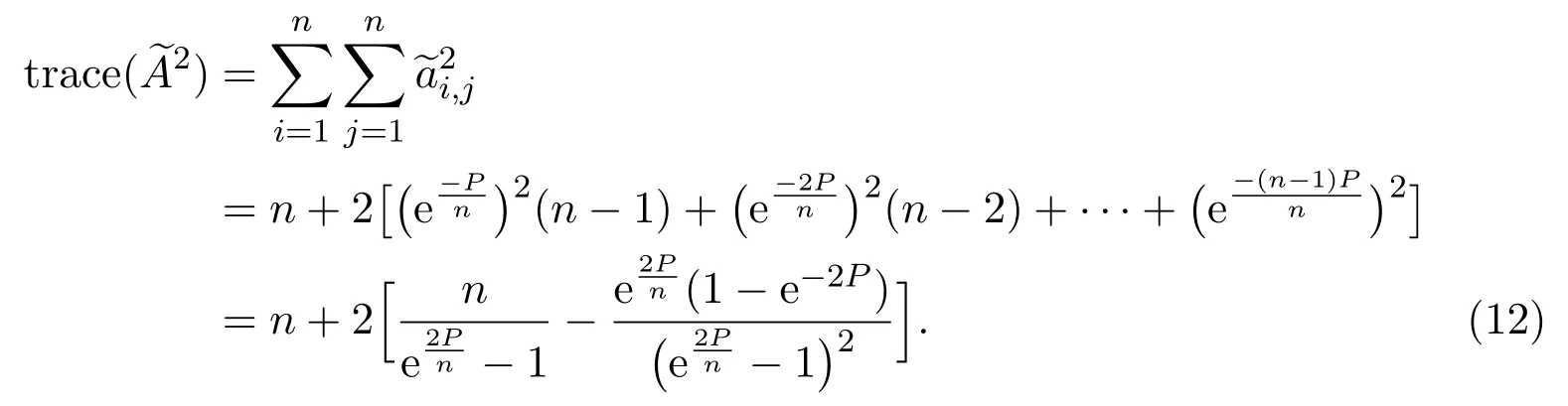
Secondly,

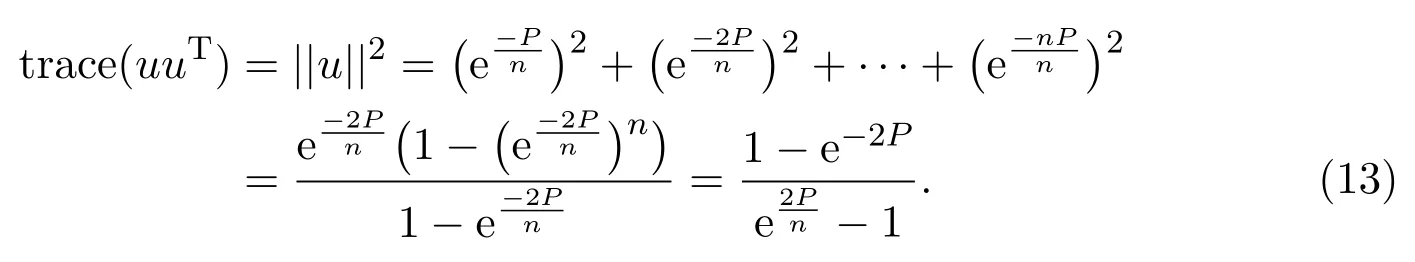
Hence,

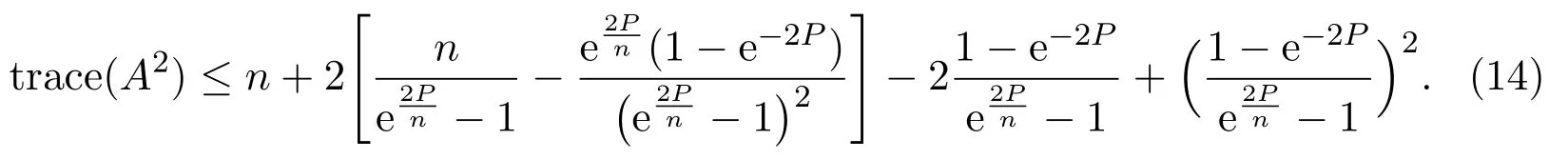
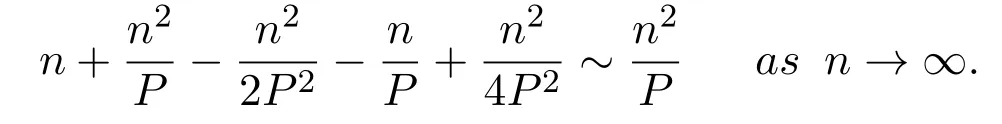
From the above analysis,we have the following conclusion:

Theorem 3is bounded by

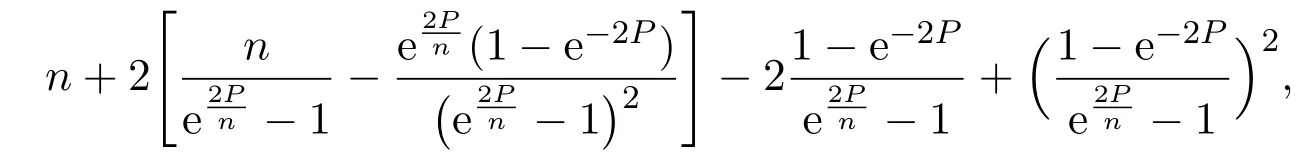
Figure 2: vs the upper bound.

4 Conclusions

In this paper,we have considered the asymptotic eigenvalue estimations for a class of structured matrices arising from statistical applications.The estimations are illustrated to be tight as n tends to infinity.These bounds are practically useful in order statistics under exponentiality.